Bonjour à tous.
Imaginons que, partant d'un triangle (la figure initiale), nous appliquions l'opération élémentaire qui consiste à séparer ce triangle en trois triangles de même forme, de longueurs 3 fois moindres, et disposés comme dans la figure ci-dessous.
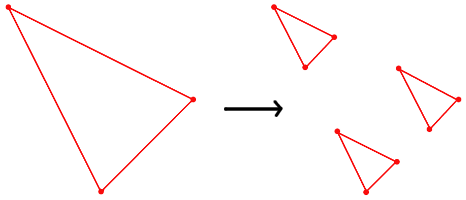
Si l'on applique à nouveau cette opération un grand nombre de fois, "à la limite", on obtient une espèce de poussière fractale ressemblant à la figure suivante, et que les érudits nomment parfois "triangle de Cantor".

Voici maintenant venir l'énigme. Je vous propose ci-dessous 3 figures fractales. Pour chacune d'entre elles, pouvez-vous trouver une figure initiale ainsi qu'une opération élémentaire qui l'engendrent ?
Fractale 1 :

Fractale 2 :

Fractale 3 :

Pour vos réponses, un dessin sera apprécié.
Indice : Spoiler : [Afficher le message] Les fractales peuvent sembler compliquées, mais à chaque fois, les opérations sont simples : des figures simples (segment, triangle...) coupées en deux ou trois.

 Accueil
Accueil
 Forum
Forum











