En me baladant sur le Web, je suis tombé sur le "paradoxe de l'obtusité"  : parmi tous les triangles possibles, quelle est la proportion de triangles acutangles ?
Un certain nombre de sites reprennent cette démonstration : dans un plan infini (*) dont tous les points sont équiprobables (**), on choisit un sommet du triangle et l'on suppose dans un premier temps que les deux autres sommets sont situés dans un cercle de rayon R autour de ce point.
Le deuxième sommet étant choisi, cela délimite deux zones :



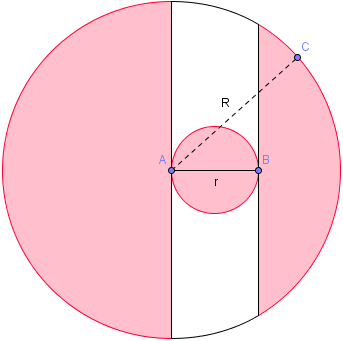
Si le troisième point est situé dans la zone blanche, le triangle est acutangle, dans la rose, il est obtusangle. Il est assez facile de montrer que la zone blanche est  trois fois plus petite que la rose, et ceci, quelque soit la valeur de R, que celle-ci tende vers r ou vers l'infini.
Ainsi, un triangle n'a qu'une chance sur quatre d'avoir ses trois angles aigus ! Étonnant, n'est-il pas ?
La démonstration parait imparable, au point que certains auteurs d'articles sur ce sujet, s'étonnent que d'autres puissent avoir l'audace de proposer une valeur différente...

Et pourtant... Si on choisit au départ deux sommets du triangle et que l'on place le centre du cercle au milieu de ce premier coté, le résultat du calcul n'est plus du tout constant en fonction de R, même si on retrouve le même résultat quand R tend vers l'infini.

Et si on choisissait les trois sommets du triangle dans un plan infini, en conservant l'hypothèse de l'équiprobabilité  ?
Je propose alors de ramener au milieu de ma feuille de papier ou de mon écran, par une habile rotation suivie d'une homothétie, le coté le plus grand de ce triangle pour obtenir la figure ci dessous :



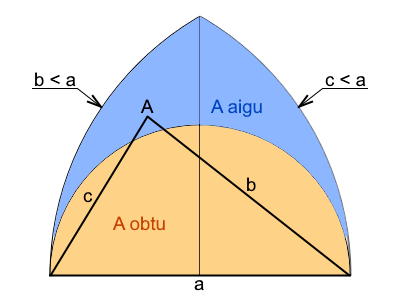
- Que devient alors la probabilité pour qu'un triangle, dont les trois sommets ont été choisis au hasard dans un plan infini, soit acutangle ?
- Comment expliquer la différence avec le résultat précédent ?

Je laisse ce topic masqué quelques jours pour que chacun puisse s'exprimer sans connaître les autres réponses.
Puis je vous laisserez vous expliquer entre vous en cas de désaccord .
  .
(*) J'aurai tendance à me méfier des calculs manipulant l'infini, autant que de ceux manipulant la valeur zéro...
(**) cette hypothèse pourrait être remise en question...