 |
#76 - 07-11-2013 15:56:52
- PRINCELEROI
- Elite de Prise2Tete
- Enigmes résolues : 33
- Messages : 1275
proba de ooker 2
"On peut voir facilement que 65 gagne aussi souvent que 76 avec une quinte"
A2345
23456
34567
45678
56789
6789T
789TJ
89TJQ
9TJQK
TJQKA
56 gagne 1 fois,perd 1 fois et partage 8 fois.
67 gagne 2 fois perd 1 fois et partage 7 fois.
Ca fait bien près de 1000 gains en plus pour 67!
je ne comprends pas.
#77 - 07-11-2013 16:28:43
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Porba de poker 2
Je dis que 65 gagne aussi souvent que 76 en faisant quinte, mais pas obligatoirement avec un tableau qui affiche quinte !
Par exemple, 65 gagne avec une quinte sur les tableaux du genre 432J9 (avec les couleurs qu'il faut) et 76 va gagner sur les aussi nombreux tableaux du genre 543QT (avec les couleurs qu'il faut)...
#78 - 07-11-2013 16:37:20
- PRINCELEROI
- Elite de Prise2Tete
- Enigmes résolues : 33
- Messages : 1275
Proba e poker 2
Mais quels types de tableaux donnent partages à 56 et pertes à 67?
#79 - 07-11-2013 18:10:48
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
prova de poker 2
Je ne suis pas sûr de comprendre ta question. Sois plus précis. Tu parles sur quels genres de tableaux ?
titoufred a écrit:Pour les partages avec une quinte affichée au tableau, je t'invite à dénombrer les tableaux JT987 qui donnent quinte à 6s5s et à AhAd. Combien y en a t-il ? Et pour 7s6s ?
#80 - 07-11-2013 18:22:55
- PRINCELEROI
- Elite de Prise2Tete
- Enigmes résolues : 33
- Messages : 1275
Proab de poker 2
Donnes moi un tableau où 56 partage et 67 perd.
S'il n'existe aucun tableau comme cela où 56 trouve-t-il ses partages de plus?
#81 - 07-11-2013 23:26:56
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Proba de pokre 2
Il n'existe pas de tableau où 6s5s partage et 7s6s perd mais peu importe.
Il existe des tableaux pour 6s5s qui n'existent pas pour 7s6s !
Tiens par exemple : JdTd9d8h7s
Et justement, il se trouve que 6s5s partage sur ce tableau...
#82 - 12-11-2013 17:04:06
- PRINCELEROI
- Elite de Prise2Tete
- Enigmes résolues : 33
- Messages : 1275
Porba de poker 2
J'ai trouvé les 24 mains!
ouais pas vite,je sais!
55566 et 55577
ouf!
#83 - 12-11-2013 20:00:38
- Klimrod
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 4054
- Lieu: hébesphénorotonde triangulaire
Prroba de poker 2
PLR : je n'ai pas compris. Peux-tu expliquer l'écart entre 5-6 et 6-7 ?
J'ai tant besoin de temps pour buller qu'il n'en reste plus assez pour bosser. Qui vit sans folie n'est pas si sage qu'il croit.
#84 - 12-11-2013 21:02:04
- PRINCELEROI
- Elite de Prise2Tete
- Enigmes résolues : 33
- Messages : 1275
Prooba de poker 2
Sur les tableaux donnant un full aux 2 mains.
AA vs (56,67)
56 gagne sur les tableaux:22255,22266,33355,33366,44455,44466.
67 gagne sur les tableaux:22266,22277,33366,33377,44466,44477,55566,55577.
#85 - 12-11-2013 21:04:59
- Klimrod
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 4054
- Lieu: hébesphénorotonde triangulaire
PProba de poker 2
J'ai tant besoin de temps pour buller qu'il n'en reste plus assez pour bosser. Qui vit sans folie n'est pas si sage qu'il croit.
#86 - 12-11-2013 21:28:41
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Proba de pkoer 2
Oui bravo PLR, c'est bien ça !
On a finalement trouvé d'où viennent les 55 victoires de plus de 7s6s par rapport à 6s5s (31 victoires sur des tableaux à 5 piques et 24 victoires par full contre full inférieur).
Maintenant, il reste à trouver d'où viennent les 885 partages de plus pour 6s5s par rapport à 7s6s. Bonne chance !
#87 - 18-11-2013 21:04:59
- Klimrod
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 4054
- Lieu: hébesphénorotonde triangulaire
PProba de poker 2
Je crois que j'ai trouvé les 885 partages supplémentaires de 6s-5s par rapport à 7s-6s.
En toit cas, j'ai trouvé un décompte qui aboutit à 885  ! !
Il faut considérer les quintes qui sont partagées. Ce sont toutes les quintes directes au tableau, c'est-à-dire A-R-D-V-10, R-D-V-10-9, D-V-10-9-8, V-10-9-8-7, 10-9-8-7-6, 9-8-7-6-5, 8-7-6-5-4, 7-6-5-4-3, 6-5-4-3-2 et 5-4-3-2-A, auxquelles il faut enlever les couleurs à Pique (gagnées par 7-6 ou 6-5) et les couleurs à Cœur ou à Carreau (gagnées par Ah-Ad).
Pour éviter des dénombrements fastidieux, on peut raisonner uniquement en écart entre 7s-6s et 6s-5s.
Tous les tableaux A-R-D-V-10, R-D-V-10-9 et D-V-10-9-8 sont équivalents vis-à-vis de 7s-6s et 6s-5s (cf ci-dessous sur fond bleu).
Tous les tableaux V-10-9-8-7, 10-9-8-7-6, 9-8-7-6-5, 8-7-6-5-4 et 7-6-5-4-3 vis-vis de la main 7s-6s sont équivalents aux tableaux 10-9-8-7-6, 9-8-7-6-5, 8-7-6-5-4, 7-6-5-4-3 et 6-5-4-3-2 vis-à-vis de la main 6s-5s (cf ci-dessous sur fond vert).
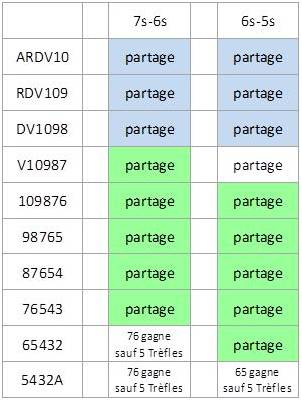
Il faut donc comparer d'un côté le nombre de tableaux V-10-9-8-7 qui permettent à la main 6s-5s de partager, auquel on ajoute le tableau 5432A à Trèfle, et de l'autre côté les deux tableaux 65432 à Trèfle et 5432A à Trèfle.
Or le nombre de tableaux V-10-9-8-7 qui permettent à la main 6s-5s de partager est égal à :
nombre total de tableaux V-10-9-8-7 = 4*4*4*4*4 = 1024
moins nombre de couleurs à Cœur = (3+3+3+3+3) +1 = 16
moins nombre de couleurs à Carreau = (3+3+3+3+3) +1 = 16
moins nombre de couleurs à Pique= (10*9) + (3+3+3+3+3) +1 = 106
Donc 1024 - 16 - 16 - 106 = 886
Finalement l'écart est donc égal à 886 +1 -2 = 885 tableaux en faveur de 6s-5s qui partage avec Ah-Ad.
Klim.
[Edit] Après discussion avec PLR, mon décompte n'était pas tout à fait exact.
Voici un autre décompte :
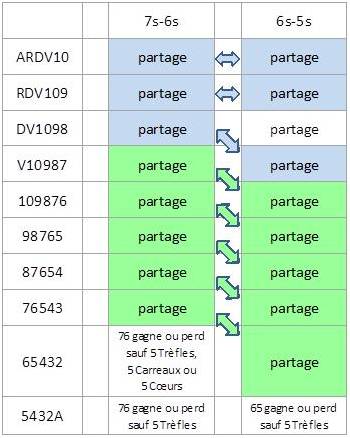
Le nombre de tableaux D-V-10-9-8 qui permettent à la main 6s-5s de partager est égal à :
nombre total de tableaux D-V-10-9-8 = 4*4*4*4*4 = 1024
moins tableaux de 4 cartes exactement à Cœur = (3+3+3+3+3) = 15
moins tableaux de 4 cartes exactement à Carreau = (3+3+3+3+3) = 15
moins tableaux de 3 ou 4 cartes exactement à Pique= (10*9) + (3+3+3+3+3) = 105
Donc 1024 - 15 - 15 - 105 = 889
Finalement l'écart est donc égal à 889 +1 -4 = 886 tableaux en faveur de 6s-5s qui partage avec Ah-Ad.
Zut ! J'en ai un de trop ! 
J'ai tant besoin de temps pour buller qu'il n'en reste plus assez pour bosser. Qui vit sans folie n'est pas si sage qu'il croit.
#88 - 19-11-2013 13:33:31
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Proba de pokr 2
Klimrod, tu y es presque !
Tu es plus proche de la solution avec ce que tu as écrit avant ton edit qu'après.
Il faut uniquement prendre en compte les tableaux qui donnent exactement la même QUINTE aux deux mains.
Indice : il n'y en a pas du tout dans tes cases blanches en bas (65432 et 5432A) !
#89 - 19-11-2013 13:47:49
- Klimrod
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 4054
- Lieu: hébesphénorotonde triangulaire
peoba de poker 2
titoufred a écrit:Indice : il n'y en a pas du tout dans tes cases blanches en bas (65432 et 5432A) !
Bah si ! Il y en a !
Ce sont toutes les quintes-flush à Trèfle, à Coeur et à Carreau (sauf qu'il ne peut pas y en avoir à Coeur et à Carreau avec le tableau 5432A, puisque les As rouges sont dans la main adverse).
J'ai tant besoin de temps pour buller qu'il n'en reste plus assez pour bosser. Qui vit sans folie n'est pas si sage qu'il croit.
#90 - 19-11-2013 13:57:43
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
proba se poker 2
Les tableaux qui donnent exactement quinte Klim, uniquement quinte !
Il ne faut pas compter les couleurs ou QF.
#91 - 19-11-2013 14:33:49
- Klimrod
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 4054
- Lieu: hébesphénorotonde triangulaire
Proba dee poker 2
Mais si je ne compte pas les quintes flush dans la colonne de gauche, alors je ne dois pas non plus les compter dans la colonne de droite.
Pour le tableau D-V-10-9-8, ce ne sont donc pas 889, mais 886 cas.
On retombe toujours sur 886 ! 
Cela dit, je crois que je vois d'où vient l'écart de 1.
Il vient des quintes flush supérieures à Pique (D-V-10-9-8 dans mon raisonnement) que l'on compte deux fois : une fois dans le décompte des 886 tableaux de quinte où 6-5 partage plus souvent que 7-6, et une fois dans le décompte des 31 tableaux de couleurs où 7-6 gagne plus souvent que 6-5.
J'ai tant besoin de temps pour buller qu'il n'en reste plus assez pour bosser. Qui vit sans folie n'est pas si sage qu'il croit.
#92 - 19-11-2013 14:59:43
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
proba de poler 2
La bonne façon de raisonner se fait en premier lieu, non pas sur les tableaux, mais sur les combinaisons obtenues par 76 / 65 qui leur permettent de battre AA ou partager.
Il faut donc se concentrer uniquement sur les tableaux qui donnent partage avec QUINTE aux deux mains.
On voit alors que la question se résume à :
Combien il y a de tableaux JT987 qui donnent partage avec Quinte à AhAd et 6s5s ?
#93 - 19-11-2013 15:17:19
- Klimrod
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 4054
- Lieu: hébesphénorotonde triangulaire
Proba de poekr 2
Non, le tableau V10987 vis-à-vis de 65 est identique au tableau DV1098 vis-à-vis de 76. En particulier, ces tableaux introduisent des cas vicieux qui ne sont pas des partages. Par exemple V-10 quelconques et 987 à Pique (en main 65), qui se dénombre de la même façon que D-V quelconques et 1098 à Pique (main 76).
C'est pourquoi mon deuxième tableau est plus juste : les parties bleues s'équilibrent une à une et les parties vertes aussi.
Simplement, comme tu l'as bien dit, il faut raisonner sur toutes les quintes n'ayant pas les cinq cartes de la même couleur.
Car si les 5 cartes sont à Trèfle, à Cœur ou à Carreau, les tableaux s'équilibrent entre 65 et 76, donc autant ne pas les compter, et si les 5 cartes sont à Pique, on les a déjà comptées dans les 31 tableaux générant des écarts à causes des couleurs.
Finalement mon décompte devient :
Le nombre de tableaux D-V-10-9-8 qui ne sont pas unicolores et qui permettent à la main 6s-5s de partager est égal à :
nombre total de tableaux D-V-10-9-8 non unicolores = 4*4*4*4*4 -4 = 1020
moins tableaux de 4 cartes exactement à Cœur = (3+3+3+3+3) = 15
moins tableaux de 4 cartes exactement à Carreau = (3+3+3+3+3) = 15
moins tableaux de 3 ou 4 cartes exactement à Pique= (10*9) + (3+3+3+3+3) = 105
Donc 1020 - 15 - 15 - 105 = 885
Ouf ! 
J'ai tant besoin de temps pour buller qu'il n'en reste plus assez pour bosser. Qui vit sans folie n'est pas si sage qu'il croit.
#94 - 19-11-2013 16:54:54
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
proba fe poker 2
Bon et bien bravo Klim, tu as bien trouvé les 885 partages qui manquaient !
La difficulté était de voir qu'il fallait raisonner en premier lieu sur les combinaisons et non sur les tableaux. Donc, chercher les partages pour un type de combinaison donné et non sur un type de tableaux donné.
Pour la petite histoire, on voit que la différence se fait sur QJT98 ou JT987, question de point de vue, mais peu importe, c'est pareil. Ces tableaux donnent autant de partages de quintes à 65 vs AA.
Bon, le raisonnement n'est pas complètement fini. Pour conclure, il faut également vérifier que 7s6s et 6s5s gagnent/partagent autant avec des carrés, brelans, 2 paires... Mais ça c'est facile.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum








