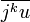Enigmes

Forum dédié aux énigmes et à toutes formes de jeux de logique.

Déconnexion

Tu n'es pas identifié sur Prise2tete : s'identifier.

accueil Accueil forum Forum
[+]

Pages: 1

Écrire une réponse

 #1 - 13-01-2012 18:11:17

Promath-
Elite de Prise2Tete
Enigmes résolues : 18
Messages : 1416
Lieu: Au fond de l'univers

Puissance à vrigules.

Bonjour!

Je me suis posé une question.
Comment fait-on pour faire des puissances à virgules?
Par exemple [latex]5^{5,67}[/latex]
Je pense qu'il faut utiliser la fonction logarithme ou une de ses dérivées et peut être son amie exponentielle?
Si quelqu'un pourrait me donner une réponse hmm

Ps: Tant que j'y suis, j'aimerais aussi savoir à quoi correspondent les traits au dessus de certains nombres comme:http://upload.wikimedia.org/wikipedia/fr/math/b/8/1/b81f17cd2f1613812b79bf046920b61d.png
Ou même un nombre plus simple surmonté d'une barre, que est ce que ca signifie?
En espérant votre aide.
Promath-

Un promath- actif dans un forum actif
    • |
  • Répondre

#0 Pub

 #2 - 13-01-2012 18:26:45

Vasimolo
Le pâtissier
Enigmes résolues : 49
Messages : 5,348E+3

Puissance à virugles.

Salut smile

Pour comprendre les exposants non entier il faut passer par les fonctions logarithmes et exponentielles : [latex]a^b=e^{b\ln(a)}[/latex] , la barre désigne le conjugué complexe .

Vasimolo

 #3 - 13-01-2012 18:37:06

Promath-
Elite de Prise2Tete
Enigmes résolues : 18
Messages : 1416
Lieu: Au fond de l'univers

Puissance à virguels.

Merci pour exponentielle! smile
Et le conjugué complexe, c'est à dire...

Un promath- actif dans un forum actif

 #4 - 13-01-2012 18:44:59

Vasimolo
Le pâtissier
Enigmes résolues : 49
Messages : 5,348E+3

uPissance à virgules.

Le conjugué de a+ib est a-ib smile

Ça ne veut pas dire grand si on ne connaît pas les notions qui sont en dessous . C'est l'équivalent de [latex]a+b\sqrt{2}[/latex] est l'expression conjuguée de [latex]a-b\sqrt{2}[/latex] mais dans un autre corps .

Vasimolo

 #5 - 13-01-2012 18:47:48

Promath-
Elite de Prise2Tete
Enigmes résolues : 18
Messages : 1416
Lieu: Au fond de l'univers

Puissance à virggules.

Merci beaucoup, Vasimolo! smilesmilesmilebig_smile
Je vais pouvoir m'en prendre aux problème complexes! smile

Un promath- actif dans un forum actif
 

Écrire une réponse

Pages: 1

Réponse rapide

Rédige ton message
| | | | Upload | Aide
:) :| :( :D :o ;) :/ :P :lol: :mad: :rolleyes: :cool:
Sécurité

Répondez (numériquement) à la petite énigme suivante : 

Si il y a 63 pommes et que vous en prenez 23, combien en avez-vous ?

Sujets similaires

Sujet Date Forum
P2T
Un dîner presque P2T. par FRiZMOUT
30-06-2010 Blabla
P2T
Robot Unicorn Attack Heavy Metal par EfCeBa
22-11-2010 Blabla
P2T
Ne floode pas qui veut par LeSingeMalicieux
29-07-2010 Blabla
P2T
Merci au cercle des sages par perceval
30-11-2008 Blabla
P2T
Merci Prise2tête par amgine
28-08-2017 Blabla
P2T
Forum Schmilblick par swoop
01-08-2008 Blabla
P2T
Fini! par PaulK
12-02-2008 Blabla
P2T
Proposition d'énigmes par cyche
11-06-2013 Blabla
P2T
De la symétrie des miroirs par hlbnet
09-07-2009 Blabla

Mots clés des moteurs de recherche

Mot clé (occurences)
Puissance a virgule (19) — Puissance avec virgule (5) — Puissances a virgules (3) — Puissance a virgules (3) — Puissance nombre a virgule (3) — Puissances a virgule (3) — Puissance et virgule (2) — Puissance virgule (2) — Les puissances avec virgule (2) — Puissance chiffre a virgule (2) — Puissance avec chiffre a virgule (2) — Ca existe les puissances a virgule (1) — Puissace 2 avec nombre a virgule (1) — Puissance 2 a virgule (1) — Puissance a viergule (1) — Puissance avec exposant a virgule (1) — Barre surmontant chiffre (1) — Chiffre puissance a virgule (1) — Puissance nombre avec virgule (1) — Calculs sur la puissance avec virgule de ph (1) — Puissance chiffre virgule (1) — Puissance avec nombre a virgule (1) — Puissane a virgule (1) — Ecrire une puissance a virgule en php (1) — Puissance avec virgule ? (1) — Calculer puissance a virgule (1) — Les puissances a virgule (1) — Puissance de chiffre a virgule (1) — Puissance a virgule de tete (1) — Pourquoi une virgule chiffre en puissance (1) — Mathematique puissance a virgule (1) — Puissance avec des virgules (1) — Mathematique nombre surmonte d une barre (1) — Chiffre surmonte d une barre (1) — Math puissance a virgule (1) — Passer de puissance a virgule (1) — Les puissances avec des virgules (1) — Pussance virgule (1) — Les puissances de chiffres a virgule (1) — Math puissance avec nombre a virgule (1) —

Pied de page des forums

P2T basé sur PunBB
Screenshots par Robothumb

© Copyright 2002–2005 Rickard Andersson
Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact
© Prise2tete - Site d'énigmes et de réflexion.
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.
Flux RSS de Prise2Tete Forum Jeux & Prise2Tete Test & Prise2Tete Partenariat et Publicité sur Prise2Tete