 |
#1 - 15-01-2024 13:31:21
- LeJeu
- Passionné de Prise2Tete
- Enigmes résolues : 25
- Messages : 92
Les 17 ponnts
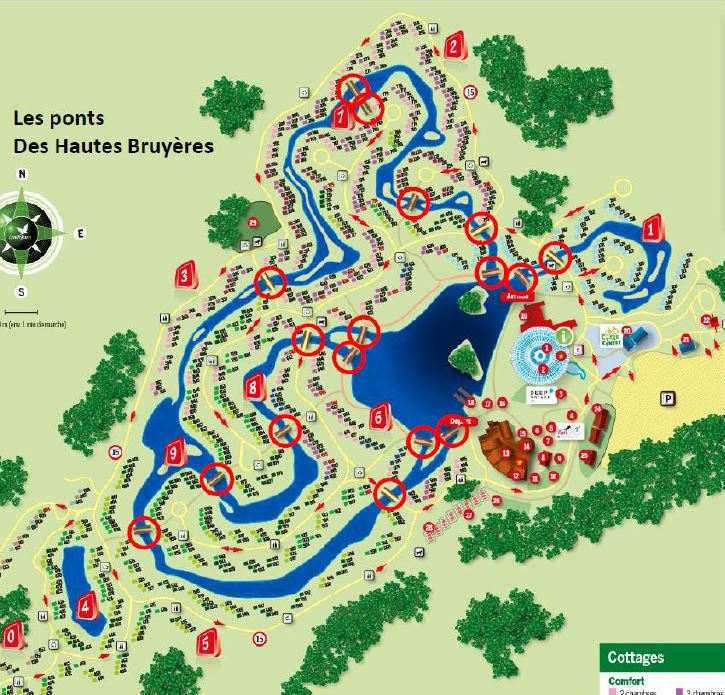
On considère les iles et les 17 ponts de Hautes-Bruyères illustrés ci-après.
Est-il possible d’effectuer un parcours qui traverse chacun des 17 ponts ( une fois et une seule chaque pont) avec un point de départ distinct du point d’arrivée ?
Si oui choisir un point de départ et recenser le nombre de parcours différents correspondants
La case réponse attend ce nombre
Le Jeu
[Edit] Précision : on ne prend en compte que la topologie des iles et des ponts : on ignore bien sûr les chemins/routes et leur sens de circulation que l'on devine vaguement en fond de carte , pas plus que l'on ne s'occupe des sens interdit dans le problème des Ponts de Konisberg !
#2 - 19-01-2024 16:20:34
- LeJeu
- Passionné de Prise2Tete
- Enigmes résolues : 25
- Messages : 92
Les 17 pots
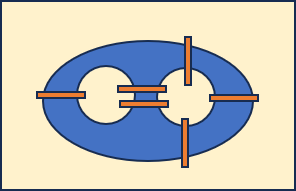
[Un exemple] c'est calme coté propositions..
Plus simple, ci dessous il y a 6 ponts et ... 72 chemins possibles
Si ça peut aider..
#3 - 26-01-2024 10:50:20
- LeJeu
- Passionné de Prise2Tete
- Enigmes résolues : 25
- Messages : 92
Les 17 pots
Bonjour,
L'énigme n'a pas trouvé son public..
je la laisse donc ouverte vivre sa vie !
Le Jeu
#4 - 26-01-2024 15:32:24
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
Les 17 pnts
Je trouve : 79488000 (qui a priori est validé par la case réponse)
En gros: On simplifie tout ça sous forme de graphe. Certains ilots peuvent être éliminés, on se retrouve en gros avec 3 pâtés A, B et C, avec
* 3 ponts entre A et B
* 4 ponts entre A et C
* 5 ponts entre B et C
* 2 ponts de B à lui-même
On peut donc passer par tout une et une seule fois, à condition de démarrer en A et de finir en C (ou l'inverse).
On peut virer les ponts de B vers B: on passe 4 fois sur le pâté B via les autres ponts (8 ponts vers / depuis B, donc 4 passages). Donc on peut calculer "1 parmi 4 + 2 parmi 4" = 10 pour tous les endroits où on peut glisser des trajets de B vers B (on peut faire les deux en une fois, ou sur deux passages)
Et on multiplie par 2! pour l'ordre de ces ponts --> total 20.
On multipliera le résultat final par 20.
Il reste
* 3 ponts entre A et B
* 4 ponts entre A et C
* 5 ponts entre B et C
On définit la fonction f(ile, ab, ac, bc) =
* f(A,0,0,0) = f(B,0,0,0) = 0
* f(C,0,0,0) = 1
* f(A,ab,ac,bc) = ab * f(B, ab-1, ac, bc) + ac * f(C, ab, ac-1, bc)
* f(B,ab,ac,bc) = ab * f(A, ab-1, ac, bc) + bc * f(C, ab, ac, bc-1)
* f(C,ab,ac,bc) = ac * f(A, ab, ac-1, bc) + bc * f(B, ab, ac, bc-1)
Avec ces récurrences, on peut calculer f(A, 3, 4, 5) et on trouve 3974400
Multiplié par 20 pour ajouter les trajets de B vers B: on trouve 79488000
#5 - 26-01-2024 17:46:24
- LeJeu
- Passionné de Prise2Tete
- Enigmes résolues : 25
- Messages : 92
es 17 ponts
Bonjour Scarta,
Évidemment, si la case réponse valide 79 488 000 c'est que c'est la bonne réponse !
L'explication donnée par Scarta est parfaite : le schéma, le nombre de ponts, le facteur 20 donné par les deux ponts de B vers B ,et le calcul de f(A, 3, 4, 5) par récurrence puis par programme : Bravo.
Si quelqu'un veut se lancer, reste éventuellement à calculer f(A, 3, 4, 5) par dénombrement, combinatoire..
Le Jeu
#6 - 27-01-2024 22:31:38
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
Lse 17 ponts
En version combinatoire : en gros, il faut considérer deux cas:
* soit il n’y a pas de ABA.
Donc tous les AB sont des ABC (donc des AC), et tous les BA sont des CBA (donc des CA, donc des AC aussi en fait).
- On choisit 3 BC parmi 5, et avec les 3 AB on forme 3 AC --> facteur 5 x 4 x 3
- On a 7 AC et 2 BC, qui vont servir à faire
--- un aller AC
--- puis 4 allers-retours CAC ou CBC
- Ce qui revient à faire 7! pour l'ordre des AC, 2! pour l'ordre des BC, et C(1,4) pour placer l'aller-retour CBC au milieux des autres.
--- > On arrive à 5 x 4 x 3 x 7! x 2! x 4 = 4 x 7! x 5!
* soit on a ABA (une seule fois, pas possible de faire plus)
On choisit 2 AB pour savoir lesquels feront cet aller-retour (facteur 3x2)
On combine le AB restant avec un BC pour former un AC (facteur 5)
On a 5 AC, 4 BC et un aller-retour ABA qu'on traitera en dernier.
- un aller AC
- 4 allers-retours CAC ou CBC
Ce qui revient à faire 5! pour l'ordre des AC, 4! pour l'ordre des BC, et C(2,4) pour ordonner ces allers-retours.
On a pour l'instant 6 x 5 x 5! x 4! = 6! x 6!
Reste l'aller-retour ABA, qui peut arriver sur n'importe lequel des 3 A qu'on parcourt : facteur 3
--- > on arrive à 3 x 6! x 6!
Total: 5! x 5! x (168 + 108) = 5! x 5! x 276 = 3974400
(et le tout fois 20 pour finir)
#7 - 29-01-2024 06:51:33
- LeJeu
- Passionné de Prise2Tete
- Enigmes résolues : 25
- Messages : 92
Les 177 ponts
Parfait Scarta !
Remarque
Bien sûr le résultat s'exprime aussi en fonction des 3 factorielles
F( A,3,4,5) = 3!*4!*5! *230
( ce qui est normal car ce sont les choix qui s'offrent quand on a décidé vers quelle ile on va)
Mais aussi, plus précisément : ( les deux 5! du résultat de Scarta)
F( A,3,4,5) = 3!*(4+1)!*5! *46
expression qui reste vraie
F( A ,ab, ac, bc) = ab! (ac+1)! bc! * X
avec ab et bc impair, ac pair
bien sûr reste à déterminer X...
#8 - 29-01-2024 11:47:55
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
Les 17 ponnts
Si on définit [latex]i[/latex] le nombre d'allers-retours ABA qu'on fait en pratique, ça doit donner un truc comme :
[TeX]ab! * bc! * ac! * \sum_i{C_{ac+ab-2i}^{ab-2i} * C_{\frac{ac+bc-1}{2}}^{\frac{bc-ab}{2}+i} * C_{\frac{ab+ac-1}{2}}^{i}}[/TeX]
avec i compris entre max(0, ab-bc)/2 et min(ab-1, bc-1)/2
Pour 3,4,5 :
6 x 24 x 120 x [C(3,7) x C(1,4) x C(0,3) + C(1,5) x C(2,4) x C(1,3)
6 x 24 x 120 x [35 x 4 x 1 + 5 x 6 x 3]
= 3974400
Le premier C() correspond au nombre de combinaisons pour placer les "ABC" (pseudos AC) parmi les autres AC
Le second C() correspond au nombre de combinaisons pour placer les aller-retours CBC parmi les allers-retours CxC
Le dernier C() correspond au nombre de combinaisons pour placer les aller-retours ABA parmi les différents A disponibles
|
 |

 Accueil
Accueil
 Forum
Forum








