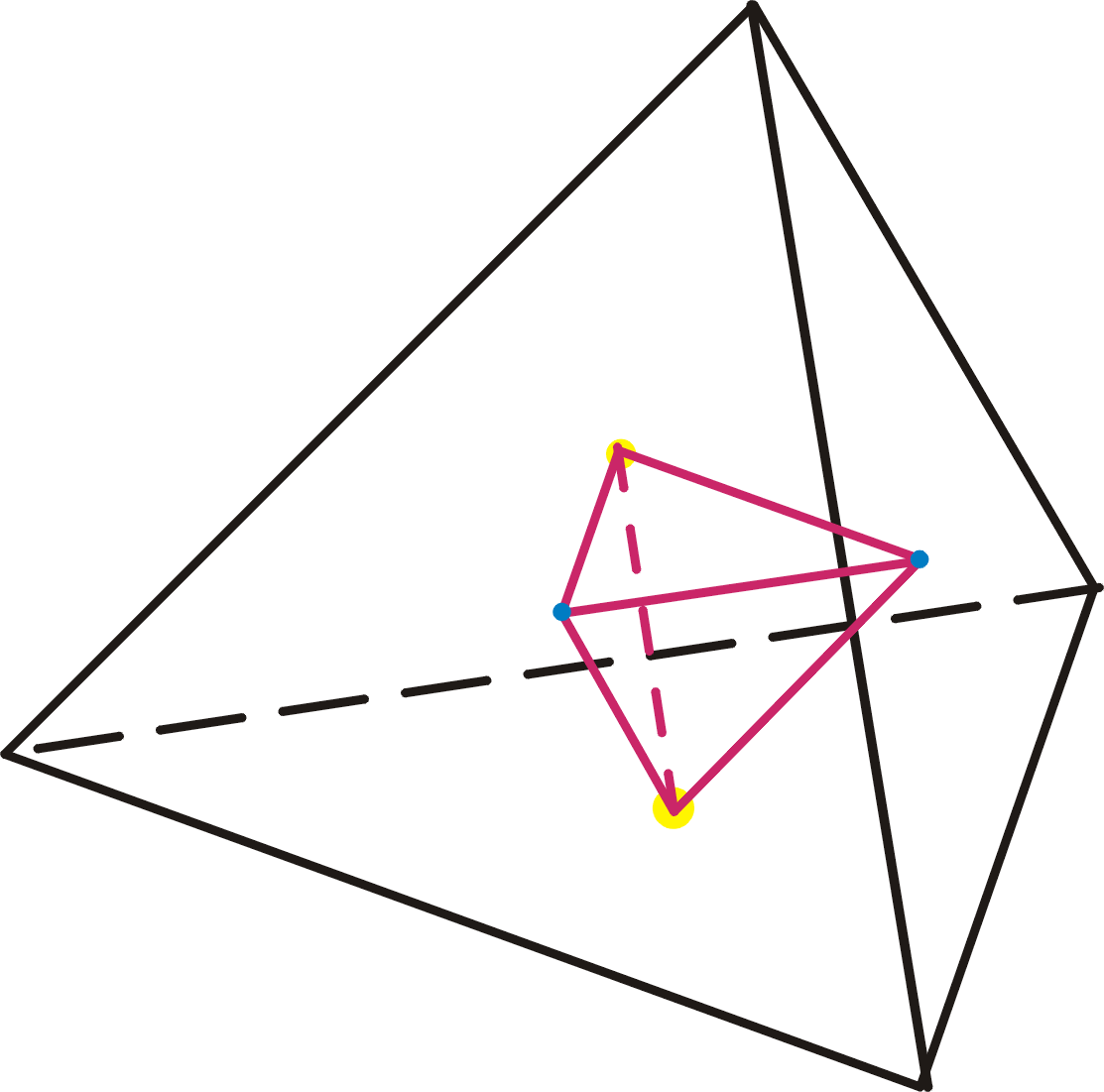
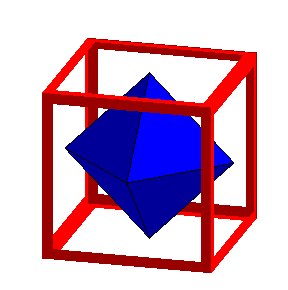
Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
© Prise2tete - Site d'énigmes et de réflexion.
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.