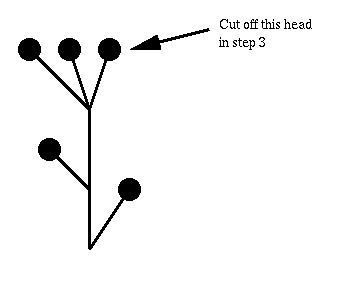|
#1 - 09-12-2011 11:46:04
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Clydevil's mathematical beestiary
Hello, j'avais envie de me faire mon petit topic blabla pour partager divers monstres mathématiques qui m'ont marqué un jour. Un nouveau monstre de temps en temps lorsque j'aurais envie d'écrire.
Il n'y a pas réellement de classement dans ceux ci ils auront un numéro qui ne correspondra qu'à l'ordre dans lequel je m'en rappelle.
Monstre 1: Le paradoxe de Banach Tarski
Énoncé choquant du théorème:
Si on considère la boule unité en dimension 3 (donc la boule tout à fait commune de l'ensemble des points de R^3 dont la distance à l'origine est inférieure ou égale à 1) il est possible de découper cette boule en 6 morceaux (au sens partition, on a donc 6 ensembles de points, un point de la boule étant dans un seul et unique morceau) de tel sorte que par uniquement translation et rotation de ces morceaux, sans aucune déformation, contraction ou dilatation de ceux ci on puisse reformer, à la manière d'un puzzle, deux boules de même taille que l'originale(Sans bien sur qu'il ne manque aucun point à l'une d'entre elle ni qu'aucun point de deux morceaux ne se chevauche, nous parlons ici de boule et une boule c'est plein, qu'il n'y ait pas d'ambiguïté)
Pour que la folie de la chose soit claire je le redis d'une autre manière, oui en découpant en morceau on peut les rassembler sans les déformer pour que le volume de ce qu'on a réalisé ait doublé.
Il est plus que naturel de refuser catégoriquement ce "monstre" donc j'ajouterais quelques éléments pour convaincre le profane et le dubitatif 
Éléments de démonstration:
Bon déjà quelque chose de relativement étrange est qu'avec un disque sur R^2 ce théorème ne s'applique plus! Il faut 3D pour que certain phénomènes lies aux opérations de rotation aient lieu. Cependant en 2D on peut comprendre certains mécanismes: Imaginez que vous enrouliez sur un cercle la demi droite discrète des entiers naturels, en prenant soin de choisir un cercle ou vos points ne se chevaucheront jamais, ceci forme un nuage de poins dense sur le cercle. Vous remarquez maintenant que si vous retirez les points des entiers de 0 à un N donné et que vous tournez le nuage restant, alors vous pouvez faire en sorte de retrouver le nuage initial sans aucun point manquant, et c'est ce genre de propriété qui est utilisé dans le théorème.
#2 - 09-12-2011 14:31:56
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
Clydevil's mathematicaal bestiary
Bien sûr, chacun des 6 morceaux de cette partition n'est pas mesurable au sens de Lebesgue ! Sinon la théorie de la mesure de Lebesgue serait contradictoire...
Plus simplement parler du volume de l'un des morceaux n'a pas de sens.
#3 - 09-12-2011 15:26:38
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Clydevil's amthematical bestiary
@masab: C'est exact, chaque morceau est un nuage de point pour lequel la notion de volume n'a pas de sens. Ce qui n'empêche pas la propriété d'être assez extraordinaire et terriblement contre intuitive  . .
Monstre 2: La loi de Benford
Un petit monstre mais également très contre intuitif.
Imaginez que vous construisiez une immense base de donnée de mesures de toute sorte. (En base 10 comme on a l'habitude de compter) vous y notez un peu tout et n'importe quoi, la longueur des objets de votre bureau en kilomètres si ca vous fait plaisir, la température des planètes du système solaire, la vitesse d'écoulement de l'eau dans chaque cour d'eau de France etc... Un gros tas de mesures variées dans des unités totalement arbitraires et diverses.
Ensuite vous les classez par premier chiffre significatif, (ce qui fait donc 9 possibilités), il est naturel de s'attendre à trouver 11% de chaque n'est ce pas, étant donné le caractère totalement aléatoire du protocole, et bien non, un phénomène étonnant se produit vous aurez autour de 30% de premier chiffre significatif 1 et 5% de premier chiffre significatif 9, le pourcentage baissant plus le chiffre significatif considéré est grand.
Éléments de démonstration:
La démonstration de celui ci est assez bluffante tellement c'est "évident", en fait lorsque vous avez constitué votre base de donnée de mesure il n'y a pas une seule source d'aléatoire, il n'y a pas que les grandeurs qui soient choisies au hasard mais également l'unité de mesure qui évidemment change tout. Donc imaginez pour simplifier les choses qu'on ait que des données dans la même unité, l'intuition nous dit qu'on devrait trouver 11% de chaque type de premier chiffre significatif, et cette intuition devrait encore être vraie si on changeait l'unité de toute nos mesures. Mais avec 11% de chaque le changement d'unité bouleverserait absolument toute notre statistique, car cette distribution n'est pas "scale invariant" elle dépend de l'unité de mesure, et ce qu'on vient de démontrer c'est que s'il y a une distribution récurrente ca ne peut pas être 11% etc... En fait la seule distribution qui convienne est une sorte de distribution logarithmique.
#4 - 12-12-2011 09:36:48
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
clydevil's mathematical bestuary
#5 - 15-12-2011 18:04:19
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Clydevil's mathematical bsetiary
#7 - 21-12-2011 09:31:56
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Clydevil's mathematical bestiayr
En espérant que quelqu'un le lira,
que celui ci le comprendra et aura appris quelque chose,
et que ca lui plaira...
Monstre 5: La théorie des ensembles
La théorie des ensembles, et oui tous le monde pense savoir ce que c'est et pourtant très peu de gens ont compris la portée de la chose. Oui la théorie des ensembles c'est exactement ce que vous imaginez, des objets mathématiques qui peuvent "contenir" d'autre objets mathématique, avec les opérations d'union d'ensemble, d'intersection etc... les fameux "pour tout" et "il existe" etc...
Mais lorsqu'on sait cela et uniquement cela, on a absolument rien vu de ce en quoi c'est révolutionnaire. Alors je propose ici de tenter de l'expliquer.
Un ensemble en mathématique c'est en partie ce qu'on vient de dire, quelque chose qui peut "contenir" d'autre chose, et comme notre but ici est de définir le minimum, ces autres choses seront également des ensembles.
On définit les ensembles par plusieurs propriétés qu'on admet vraies par définition, on appelle ceci des axiomes. Pour définir quelque chose on revendique généralement son "existence" et c'est ainsi que sont construit les axiomes de la théorie des ensembles:
Par exemple:
Axiome de la réunion: Pour tout ensemble X, il existe un ensemble R dont les éléments sont précisément ceux des éléments de X et eux seuls.
Ce qu'il faut retenir de cet exemple c'est qu'avec cet axiome qu'on revendique vrai on définit à la fois un peu le monde des ensembles, en décrivant une de leur propriété, mais également ce qu'on nomme l'union et l'appartenance dans cet univers. Avec d'autres mots, les termes s'auto-définissent.
Pour construire le monde couramment utilisé des ensembles on a au total besoin d'une dizaine d'axiome. Avec avec eux on définit ce qu'est un ensemble, a travers les propriétés qu'il entretient avec ces camarades.
L'intérêt du monde des ensembles est qu'il est suffisamment souple pour représenter tout objet des mathématiques modernes, avec cette phrase j'ai déjà tout dit mais pour le lecteur manquera sans doute le Eureka, alors un exemple:
-mettons l'étiquette "0" sur l'ensemble vide. (Un ensemble particulier dont on clame l'existence/qu'on a défini via les axiomes de notre théorie)
-mettons l'étiquette "1" sur l'ensemble des parties de l'ensemble vide (dont on clame également l'existence/qu'on a défini via les axiomes de notre théorie)
-mettons l'étiquette "2" sur l'ensemble des parties de l'ensemble étiqueté 1...
etc... pour chaque entier.
Jusque la rien de dingue on a simplement et de manière arbitraire établit une correspondance entre nos entiers et des ensembles. Tentons plus compliqué, représenter une fonction avec un ensemble. Un fonction n'est rien de plus que l'ensemble de ses couples antécédent/image. L'astuce pour noter le couple (a,b) avec un ensemble ou il n'y a pas de notion d'ordre c'est {a,{a,b}}
Prenons la fonction qui va des entiers dans les entier et qui a x associe sont carré (x->x^2).
{
{1,{1,1}}
{2,{2,4}}
{3,{3,9}}
...
}
Et comme on a déjà représenté chaque entier avec des ensembles on pourrait remplacer dans ceci les "1" ou les "9" etc par ce qu'on a déjà construit et bien avoir une structure constitué uniquement à base d'ensembles.
L'opérateur + n'est rien d'autre qu'une fonction ZxZ->Z donc de la même manière on pourrait très bien le construire en vision purement ensembliste.
La correspondance entre concept et ensemble est arbitraire, mais on peut toujours en choisir une utilisable et naturelle comme ci dessus. Tous les objets conceptuels logiques que ca soit l'opérateur x ou intégrale, ou un "triangle", ou une suite d'entier, ou la fonction sinus, sont facilement "mappable" sur des ensembles. Ce ne sont que des étiquettes qu'on a choisit de poser arbitrairement sur certains d'entre eux.
L'intérêt des objets en mathématique ce ne sont pas ce qu'ils sont de manière isolé mais les propriétés qui les relie l'un à l'autre. Le théorème de Pythagore par exemple est une propriété d'un triangle relié avec nos notion de longueur et de réels etc...
La folie en fait c'est que lorsqu'on a mappé nos concepts usuels a des ensembles, alors rien qu'avec les axiome de cette théorie, les ensembles, traduction de nos concepts, vont se comporter entre eux comme leur homologues. Autrement dit, le théorème de Pythagore que je viens de citer, une fois tous les concepts construit en tant qu'ensembles vous pouvez
le démontrer en avec uniquement la dizaine d'axiome de la théorie.
Bien sur ca serait une démonstration extrêmement longue mais le point important n'est pas de la faire, simplement savoir qu'on peut, on a trouvé un formalisme extrêmement concis (une dizaine d'axiomes), qui permet de représenter tout concept et de modéliser tout raisonnement connus des mathématiques. Comme mon but est de faire "tilter" le lecteur, je le redis encore une fois, quelque soient les concepts en mathématiques que vous ayez manipuler entre votre CP et votre bac ou votre prepas, ils sont représentables
par des ensembles et les propriété qui relient ces représentations avec uniquement la dizaine d'axiomes ensemblistes sont les mêmes que celles de leur homologues.
Et c'est ceci la révolution, comment aurait-on pu imaginer que quelque chose d'aussi libre que nos abstractions de tout genre et démonstrations puissent être mathématisé avec les mêmes et très peu de briques de bases? ZFC est sans doute l'une des plus grande prise de conscience de mathématiques modernes, arrivé à un stade ou les mathématiques sont parvenues à modéliser
les mathématiques...
Et ca a ouvert la voie à pas mal de découvertes monstrueuses...
#8 - 21-12-2011 12:13:03
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Clydevil's mathematical bestiiary
#9 - 21-12-2011 13:48:56
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
clydevim's mathematical bestiary
Et certainement une bien plus grande infinité 
- Dire que la théorie des ensembles génère des monstres c’est prendre le problème à l’envers : cette théorie a justement été créée pour tordre le cou aux multiples paradoxes qui décrédibilisaient les mathématiques.
...
Les monstres ne sont pas forcément générés par la théorie , ils existent par eux même
C'est à cause du titre du topic? en tout cas ce n'est pas ce que je voulais dire alors, je suis parfaitement d'accord avec toi. Pour moi "monstre" n'était pas du tout péjoratif et ils existent par eux même, oui, c'est juste que dans un cadre nettoyé on a réussi à les trouver la ou avant ils se cachaient. Je parlerais bientot d'incomplétude de Godel  (ce qui est sans doute ce à quoi tu faisais allusion, ou du même genre, lorsque tu dis que les axiomes ne font pas tout) (ce qui est sans doute ce à quoi tu faisais allusion, ou du même genre, lorsque tu dis que les axiomes ne font pas tout)
#10 - 21-12-2011 19:53:41
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
cmydevil's mathematical bestiary
J'apportais mon petit grain de sel ( ou de sable ) à ton fil , n'y voit pas d'offense . J'adore le thème 
Vasimolo
#11 - 18-01-2012 09:14:08
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
vlydevil's mathematical bestiary
Monstre 6: Prévoir le hasard.
Imaginez une infinité de boites numérotées, avec dans chacune, un nombre entier choisi totalement arbitrairement. Vous avez le droit d'ouvrir les boites de votre choix, y compris une infinité, pour y découvrir l'entier caché, mais vous devez laisser au moins une boite pour laquelle avant son ouverture vous ferez une prédiction sur son contenu. Un protocole qui semble bien loufoque n'est ce pas? comme si on pouvait prédire le hasard... He bien l'un des plus beau paradoxe que j'ai vu est qu'on peut pourtant trouver un protocole pour prédire le contenu de notre boite avec un niveau de certitude arbitrairement grand. (ie: si vous désirez avoir juste pour votre prédiction dans 9 cas sur 10 ou 99 cas sur 100 vous pouvez...)
Évidemment, ceci nécessite des capacités exotiques, comme mémoriser une infinité non dénombrable de certaines choses, mais ca n'en reste pas moins extrêmement étrange de pouvoir prédire le hasard en consultant des variables sans rapport théorique entres elles....
Pour rendre à César ce qui lui appartient je propose une adaptation plus ludique du même paradoxe:
http://www.madore.org/~david/weblog/200 … 05-16.1643
"Le docteur No continue ses méfaits"
#12 - 18-01-2012 19:39:22
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Clydevil's mathematical bestiaryy
A l'âge de 10 ans je m'étais déjà posé la question de savoir si oui où non il était possible "d'inverser" une sphère. Je pensais que non. Et bien j'ai eu ma réponse. Mais tout cela n'est pas concevable dans un monde comme le notre, on ne peut pas traverser la matière, enfin on peut mais la probabilité qu'un atome le fasse rend impossible que des milliards de milliards puisse le faire.
PS : J'ai pas compris le premier, j'en avais déjà entendu parler, mais je ne vois pas comment c'est possible. Peut-on parler de volume? Parce que 1=1+1 je ne voudrai contrarier personne mais c'est faux.
Shadock 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#13 - 18-01-2012 19:53:12
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Clydevil's mathematical besitary
Je connaissais ce sujet et il s'agît plus d'une vue de l'esprit que d'un véritable problème . D'un autre côté c'est en poussant les maths à leurs limites qu'on comprend pourquoi elle ne représenteront jamais vraiment notre quotidien ( ce n'est d'ailleurs pas son objectif ) .
Quelqu'un a déjà vu un point , une droite ou un cercle ( je rappelle que tous ces objets n'ont pas d'épaisseur ) ?
Vasimolo
#14 - 18-01-2012 22:34:38
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Cldyevil's mathematical bestiary
Et quand bien même il en aurait une, un cercle parfait n'existe pas dans la nature sauf si on le prend sur un électron qui est désespérément rond.
Shadock
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#15 - 19-01-2012 09:09:35
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Clydevvil's mathematical bestiary
@Shadock: Peut-on parler de volume? Parce que 1=1+1 je ne voudrai contrarier personne mais c'est faux.
Ce qui est beau c'est que la notion de volume ne pose pas de probleme. Les "parties" de notre découpage de boules, sont des nuages de points, et assez exotiques. (Aussi exotique que de dire "je considère les irrationnels du segment [0,1]) Par conséquent on découpe notre sphère de volume V avec nos parties bizarres pour lesquelles la notion de volume n'a pas de sens indépendamment sur chacune d'entre-elles (ie: c'est quoi la longueur des irrationnels du segment [0,1]? -> pareil, pas de sens). Et on les re-assemble d'une nouvelle manière pour former les deux sphères de volume 2xV. Sans avoir eu d'incohérence au niveau de cette notion. Relis bien mes "éléments de démonstration" tu verras c'est moins dingue qu'on imagine, ca vient principalement du fait que R^3 est infiniment divisible.
#16 - 21-05-2012 11:25:26
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Clydevil's mathematica bestiary
Monstre 7: L'incomplétude de Godel.
Vous savez le truc qui montre qu'il existe des propriétés non démontrables...
Tout d'abord pour être familier avec certains concepts je conseille de lire le monstre sur la théorie des ensembles plus haut. Mais je rappelle tout de même rapidement ici ce qu'il faut savoir:
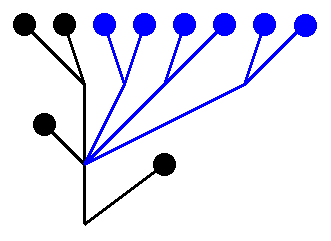
Lorsqu'on construit une théorie, l'approche moderne consiste à réunir un certain ensemble d'axiomes (ie: propriétés/principes admis par définition) et de règles de déductions élémentaires. Dans une telle théorie, une "démonstration" n'est rien d'autre qu'un arbre dont les feuilles sont piochées dans les axiomes de notre théorie et dont la morphologie correspond à la manière de les relier pour aboutir à la propriété qu'on voulait démontrer.
Je ne vais pas démontrer ici exactement le théorème de Godel, ni coller à la première demo historique (que je trouve pénible) je donne une sorte de vulgarisation aboutissant à la vérité choquante qui nous intéresse.
Lemme préliminaire:
Peut on construire un programme HALT(x,y) qui étant donné un programme x et une donnée y finira par répondre correctement à la question "Le programme x s'arrête sur la donnée y?" ?
La réponse est non, démonstration en mode speed:
Supposons qu'un tel programme HALT(x,y) existe et considérons le programme suivant:
BREAK(x):
Si HALT(x,x) tourner en boucle infiniment
Sinon s'arrêter.
Question est ce que BREAK(BREAK) s'arrête? -> je vous laisse conclure et voir le paradoxe.
Conclusion l'hypothèse de base était fausse, il n'existe pas de tel programme HALT.
Revenons à nos moutons:
Considérons une théorie basée sur un ensemble énumérable d'axiomes. Par "énumérable" on veut dire qu'il y en a soit un nombre fini, soit une infinité dénombrable mais un peu particulière: ie vous pouvez la construire depuis un nombre fini d'informations, ie vous pouvez faire un programme qui fournit un par un les axiomes". En gros "que vous pouvez définir" ce qui est tout de même naturel et plus sympa.
Dans une telle théorie il y a une infinité dénombrable de démonstrations, énumérables également, ie c'est à dire que vous pouvez construire un programme les parcourant une à une en étant sur qu'une démonstration donnée sera un jour atteinte. (Vous pouvez voir les démonstrations comme des arbres et imaginez que vous considérer d'abord les arbres une feuille puis les arbre une branche une feuille etc...)
Donc il serait possible de coder un programme SOLVER(P), associé à un ensemble d'axiomes, qui étant donnée une propriété P parcourrait toutes les démonstrations et s'arrêterait des qu'il trouverait une démonstration de P ou de non P. Certes ceci prendrait du temps mais si on considère que soit P soit non P est démontrable alors un jour le programme s'arrêtera.
Seulement voila, la terminaison d'un programme est une propriété mathématique comme le reste, si ca vous gène vous pouvez imaginer qu'un programme c'est simplement une suite d'entiers définie par récurrence. (La mémoire à un instant donnée n'étant rien d'autre qu'un terme de cette suite d'entier, et la relation de récurrence aussi complexe soit elle n'étant rien d'autre que celle qui correspond à l'exécution d'une instruction dans cette mémoire)
Ainsi on dispose d'une bonne famille de propriété de la forme F_ARITHMETIQUE:
La suite d'entiers machin définie par récurrence comme suit, et de premier terme bidule passera par l'entier 0
On remarquera que les propriétés de cette forme n'ont rien de monstrueux, le sens commun ne peut imaginer que deux choses, soit la suite en question passera un jour par 0 soit elle n'y passera jamais.
Mais la arrive le paradoxe, comme les propriétés du genre F_ARITHMETIQUE contiennent les propriétés du genre "Le programme bidule sur la donnée machin termine" et qu'il est impossible d'après le lemme 1 de construire un programme HALT alors nécessairement notre programme SOLVER sera parfois également démuni pour démontrer ou infirmer des proprietes de la forme F_ARITHMETIQUE.
Autrement dit, vous pouvez construire l'ensemble d'axiome énumérable que vous voulez, il existera toujours des proprietes pour lesquelles vous ne pourrez ni démontrer P ni démontrer non P avec. Et en plus des proprietes non nécessairement exotiques, une propriété de la forme F_ARITHMETIQUE ca semble basique et pourtant en arrivera fatalement une pour laquelle vous ne pourrez pas répondre à la question de son passage par 0 autrement qu'en admettant un axiome supplémentaire.... le plus simple étant d'admettre la propriété en question et vous conviendrez que comme démonstration on a connu mieux...
D'autant plus que vous avez le droit d'admettre son contraire à la place si ca vous chante ca ne donnera aucune incohérence.
Donc ceci c'était à peu de chose près le principe d'incomplétude de Godel:
Dans un certains cadre (que je choisi de ne pas rigoureusement définir), tout à fait naturel, il n'y a pas d'ensemble d'axiomes énumérable satisfaisant permettant de démontrer tout ce qu'on pourrait légitimement s'attendre à démontrer.
Godel a également montré que: Dans une théorie axiomatique il est impossible de démontrer au sein même de cette théorie que l'ensemble des axiomes sur lesquelles elle est fondée n'est pas contradictoire.
Autant quand on choisit un ensemble d'axiomes incohérent on peut aboutir à une absurdité et donc s'en rendre compte autant quand ils sont a priori cohérent vous ne pouvez pas en être sur...
Ça s'applique aux mathématique modernes que vous utilisez chaque jour.
Voila voila, je mettrais à jour les passages flous de ce proof of concept plus tard.
#17 - 11-11-2012 19:05:59
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Clyddevil's mathematical bestiary
Moi j'aime bien le Théorème de Hausdorff :
La sphère unité peut être décomposée en quatre parties isométriques A, B, C, D avec D également isométrique à AuB.(D est donc à la fois le quart et le tiers de la sphère).
Choquant non? 
Shadock
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#18 - 12-11-2012 03:51:00
- Seanbateman
- Professionnel de Prise2Tete
- Enigmes résolues : 21
- Messages : 321
- Lieu: Toujours à l'énigme 3
Clydevil's mathematical bestiaryy
Juste en parlant de Gödel je vous recommande le livre Les Démons de Gödel : Logique et folie pour comprendre un peu le personnage.
Quand on ne sait rien, on peut tout de même trouver des choses, avec de l'imagination. [Boris Vian]
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum