|
#1 - 01-03-2011 19:28:24
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3612
- Lieu: 94110
empilage de briqurs - terminus
On empile des briques sur un support.
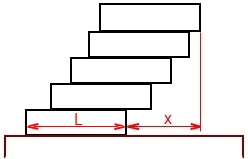
Quel est le décalage maximum x/L que l'on peut atteindre entre la première et la dernière brique avec 10 briques sans que l'édifice ne s'écroule ?
Les briques, posées à plat (une seule par niveau), ont des cotés dans les rapports L - L/2 - L/4, et sont bien sûr, infiniment rigides, avec des angles parfaitement vifs et des faces absolument planes et parallèles.
Le support est lui, parfaitement plan, horizontal et rigide, et en plus, il n'y a pas de vent, pas plus que de colle entre les briques!
Question subsidiaire : quel est le décalage maximum que l'on peut espérer atteindre avec autant de briques que l'on veut ?
La case réponse valide la réponse à la première question arrondie au plus proche, sous la forme x.xxx.
Spoiler : [Afficher le message] La connaissance des proportions de la brique est superflue : la réponse serait la même pour un cube de coté L.
Spoiler : [Afficher le message] Vous avez peu de chances de trouver si vous ne prenez pas ce problème par le bon bout.
Spoiler : [Afficher le message] Et il n'y a pas 36 manières de prendre ce problème : je n'en voit que 2 : celle qui paraît évidente au premier abord ... et la bonne !
Spoiler : [Afficher le message] Il s'agit juste de déterminer une suite, de calculer la somme de ses 9 premiers termes, puis la limite de cete somme.
#2 - 02-03-2011 01:59:48
- dylasse
- Professionnel de Prise2Tete
- Enigmes résolues : 21
- Messages : 381
Empilagee de briques - Terminus
Il faut imaginer construire la pile par le dessous...
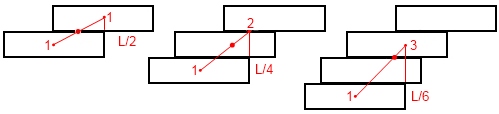
La seconde brique doit être placée sous la première, de sorte que le centre de gravité de la première (=le milieu) soit pile à l'extrémité de la seconde.
Ensuite, on place une troisième brique sous les deux premières, de sorte que le centre de gravité de la pile précédente soit juste à l'extrémité de la troisième, et ainsi de suite...
On appelle 0 la première brique, et on note En l'abscisse de l'extrémité de la brique n, on a E0=0 (choix de l'origine), et, par construction :
En = moyenne(Ei) pour i<n + 1/2.
Cette relation de recurrence équivaut à En = 1/2 somme(1/i) pour 1<=i<=n.
D'où le 1.414 pour n=9.
En tend vers l'infini lorsque l'on a suffisamment de brique.
A noter que la suite En tend lentement vers l'infini et si 5 briques on été suffisantes pour que la brique du haut ne soit plus au dessus de la première (en projection), il en faudra 32 pour avoir une brique d'écart et 228 pour avoir 2 briques d'écart, il faut donc prévoir un plafond assez haut !!!!
#3 - 02-03-2011 02:33:41
- L00ping007
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 2010
- Lieu: Paris
empilage de briqued - terminus
Problème intéressant !
Ne voyant pas comment bien matérialiser le problème, j'ai cherché quelques pistes sur le net, et en fait j'ai été étonné de voir qu'on pouvait obtenir un décalage infini avec une infinité de briques !
En effet, on décale la n-eme brique de L/2n par rapport a la verticale de celle d'en dessous. La numérotation se fait de haut en bas.
On arrive a la serie harmonique, a un facteur 1/2 près.
Pour n=10 je trouve : 7129/5040, soit environ 1.414
Et comme la serie harmonique diverge, le décalage peut être aussi grand qu'on veut.
J'imagine qu'en pratique, les contraintes de non perfection des conditions rendent la réalisation d'une telle pyramide compliquée !
J'ai trouvé ce lien très intéressant qui explique bien le problème :
http://prof.pantaloni.free.fr/IMG/pdf/S … riques.pdf
#4 - 02-03-2011 08:50:25
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3612
- Lieu: 94110
empilage de briques - teeminus
Bravos   à dylasse et à LOOping qui ont tout compris ! à dylasse et à LOOping qui ont tout compris !
Je rajoute un premier indice.
#5 - 02-03-2011 09:51:05
- gasole
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 1117
- Lieu: Toulouse
empilahe de briques - terminus
Salut Jackv,
C'est un grand classique, tout est très bien expliqué dans ce document-ci : http://prof.pantaloni.free.fr/IMG/pdf/S … riques.pdf
La formule qui donne le surplomb pour n briques est 1/2+1/4+1/6+... 1/(2n) = 1/2.H(n) où H(n) est la série harmonique dont on sait qu'elle diverge, en conséquence de quoi, le surplomb peut être aussi grand qu'on veut (tant que le support ne s'écrase pas sous le poids des très nombreuses briques nécessaires :
Cet article conclut en expliquant que ça ne prouve pas que rapporté au nombre de briques utilisées, ça soit le surplomb maximal globalement, c'est-à-dire que maximiser le surplomb à chaque étape (localement) n'est pas forcément le plus économe.
D'ailleurs, des rigolos sympathiques se sont amusés à tester d'autres façons de placer les briques et améliorent le surplomb maximal avec un nombre donnée de briques : http://www.cs.tau.ac.il/~zwick/slides/overhang.pps
En particulier, ils donnent un exemple d'empilement avec 10 briques qui atteint un surplomb de 1,78613
#6 - 02-03-2011 11:05:55
- franck9525
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1935
- Lieu: 86310
empilage de btiques - terminus
La réponse est
[TeX]d=\frac{L}{2}H_{9}\approx1.414\times L[/TeX]
en notant [latex]H_n=\sum _{i=1}^{n}\frac{1}{i}=1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{n}[/latex]
Notons que la brique 1 sert de support.
La suite harmonique diverge donc le décalage n'est pas limité mais la quantité de brique l'est certainement 
J'ai aussi posé la question à mon petit neveu et il a trouvé mieux !!! je vous raconte cela dans Badaboum 5
The proof of the pudding is in the eating.
#7 - 02-03-2011 12:28:22
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3612
- Lieu: 94110
Empilage de biques - Terminus
Bravo  et merci à Gasole qui me permet de préciser mon énoncé. et merci à Gasole qui me permet de préciser mon énoncé.
Bravo aussi à Franck  . .
#8 - 02-03-2011 14:47:30
- FRiZMOUT
- Verbicruciste binairien
- Enigmes résolues : 49
- Messages : 2218
Empilage dde briques - Terminus
Formule du décalage maximum avec [latex]n[/latex] briques :
[TeX]D_n = \sum_{x=1}^{n-1}\frac{1}{2x}[/TeX]
Pour [latex]n = 10[/latex] :
[TeX]D_{10} = \sum_{x=1}^{9}\frac{1}{2x}=\frac{7129}{5040} \approx 1,41448[/TeX]
Pour la question subsidiaire, a priori :
[TeX]D_{+\infty} = +\infty[/TeX]
#9 - 02-03-2011 17:14:09
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Empilage de briques - Termnus
Bonjour,
Quand je pose n+1 briques, il faut que le centre de gravité du bloc des n briques précédentes soit à l'intérieur de la n+1 ème brique (en comptant les briques à partir du haut, donc à l'envers).
Soit Un la distance entre le début de l'empilage et le centre de gravité du bloc de n briques: on a évidemment U1 = 0,5 et U2 = 0,75.
Calculons Un: Un = ( (n-1) Un-1 + 1 (Un-1 + 0,5) ) / n.
Soit Un = Un-1 + 0,5/n donc Un = 0,5 x somme (1/i) avec i variant de 1 à n.
Pour 10 briques, on cherche u9 = 7129 / 5040 = 1.414 environ (mais cela n'a rien à voir avec V2 !!!), validé par la case réponse.
On sait que la suite harmonique tend vers l'infini et donc, si on a une infinité de briques, alors x/l tend vers l'infini: je trouve que ce résultat va à l'encontre du bon sens élémentaire.
Bonne journée.
Frank
#10 - 02-03-2011 22:21:29
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3612
- Lieu: 94110
empimage de briques - terminus
Encore des bravos à FRIZMOUT  et à Franky1103 et à Franky1103  . .
J'ai ajouté un deuxième indice.
#11 - 03-03-2011 04:25:39
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
empilage de briques - rerminus
j'ai tapé 1.414 au hasard et ca valide..
Le décalage maximum pour chaque piece depend du centre de gravité des pieces au dessus.
il est de 0.5 pour la premiere, puis de 0.25, puis 0.167, etc... (en partant du haut)
Mais il est tard et je n'arriverais pas a 10 pour verifier 1.414...
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#12 - 03-03-2011 09:31:22
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3612
- Lieu: 94110
Empilage de briques - Terminsu
Des encouragements pour dhrm  . .
J'ai ajouté un troisième incdice.
#13 - 03-03-2011 15:51:35
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
rmpilage de briques - terminus
J'ai enfin un peu de temps. Je suis venu voir les nouveautés et je tombe sur cette énigme bien sympa sur un problème que j'aime bien mais sur lequel je n'avais jamais planché. Je m'y mets donc...
Tout est question de centre de gravité.
Un ensemble de briques en appui sur la brique de dessous doit avoir son centre de gravité (l'ensemble) au dessus de la brique de dessous ou pour maximiser l'aplomb, juste à la limite de la brique de dessous.
Le résultat est proportionnel à la longueur de la brique et puisqu'on demande le rapport x/L on peut faire les calculs avec une brique de longueur 1 pour simplifier sans changer le résultat.
D'autre part, le résultat ne dépend que des longueurs des briques, ni de la hauteur, ni de la profondeur de chacune d'entre elles du moment qu'elles ont toutes la même. En effet la position du centre de gravité sur l'axe "horizontal" sera le même.
Je fixe comme origine du repère de mesure l'extremité droite de la brique la plus haute (brique n° 1, B1) et je mesure vers la gauche.
J'appelle [latex]x_1[/latex] la distance horizontale entre l'origine des mesures et l'extremité droite de la brique n°2, B2. [latex]x_0=0[/latex] par définition de l'origine des mesures.
[TeX]x_2[/latex] est donc la distance horizontale entre l'origine des mesures et l'extremité droite de la brique n° 3 (B3), c'est-à-dire la partie en surplomb de l'ensemble B1 et B2.
On progresse de façon itérative:
La brique numéro 1 (B1) doit avoir son centre de gravité (CG) au dessus de B2 pour rester en équilibre au dessus de B2. Cela se traduit par [latex]x_1 \leq \dfrac12[/latex] et puisqu'on veut maximiser le surplomb, [latex]x_1=\dfrac12[/latex].
L'ensemble de briques B1 et B2 à son CG à une distance:
[latex]\dfrac12(\dfrac12+\dfrac12+x_1)[/latex] et pour que cet ensemble soit en équilibre au dessus de B3 il faut (et il suffit) que:
[latex]x_2 \leq \dfrac12(\dfrac12+\dfrac12+x_1)[/TeX]
et donc pour maximiser que [latex]x_2=\dfrac34[/latex].
L'ensemble de briques (B1,B2,B3) à son CG à une distance:
[TeX]\dfrac13(\dfrac12+\dfrac12+x_1+\dfrac12+x_2)=\dfrac12+\dfrac13(x_1+x_2)[/latex] et pour que cet ensemble soit en équilibre au dessus de B4 il faut (et il suffit) que:
[latex]x_3 \leq \dfrac12+\dfrac13(x_1+x_2)[/TeX]
et donc pour maximiser que [latex]x_3=\dfrac{11}{12}[/latex].
De proche en proche on calcule x4, ... et finalement x9 qui est la valeur demandée. On trouve: [latex]x_9=\dfrac{7129}{5040}[/latex], ce qui arrondi à 3 décimales donne: 1,414 qui est validé par la case réponse (pourquoi ne pas utiliser de , dans les cases réponses au lieu des .?).
Merci pour cette énigme sympathique.
Ah, oui la question subsidiaire. Aussi étonnant que cela puisse paraître, si l'on a autant de briques que l'on veut, on peut emmener le surplomb aussi loin que l'on veut, mais il faut vraiment beaucoup de briques. Cela est lié à la divergence de la série harmonique.
#14 - 03-03-2011 22:49:02
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3612
- Lieu: 94110
Empilaeg de briques - Terminus
Bravo à Rivas  pour sa démonstration. pour sa démonstration.
Et j'ajoute un 4ème indice.
#15 - 04-03-2011 01:45:29
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Empilage de briques - Terminsu
Il me semble que cet exercice est déjà apparut dans les olympiades mathématique, mais je ne me rappelle plus de l'année.
En outre j'ai quand même les capacité de le faire :
A chaque brique supplémentaire ajouté, L est divisé par deux, on a donc au n-ième rang :
[TeX]L=\frac{1}{2n}[/latex] avec n différent de 0.
Pour dix briques, le rapport x/L est donc la somme des 9 premiers termes consécutifs de la suite et on a:
[latex]\sum_{n=1}^9 \frac{1}{2n}=1.414[/TeX]
Je suis un peu confus, car je ne comprends pas trop l'énoncé L/2 et L/4 je ne vois pas ce que ça signifie 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#16 - 04-03-2011 02:28:18
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
empilage de bruques - terminus
Ok.. voila donc mes resultats:
En partant du haut:
No de brique: deplacement par rapport a la brique du haut
1: 0
2: 0.5 = 1/2
3: 0.75 = 3/4
4: 0.916667 = 11/12
5: 1.041667 = 25/24
6: 1.141667 = 137/120
7: 1.225000 = 49/40
8: 1.296429 = 363/280
9: 1.358929 = 761/560
10: 1.414484 = 7129/5040 qui ressemble a √2, mais n'est en fait qu'une fraction.
11: 1.464484 = 7381/5040
12: 1.509939 = 83711/55440
13: 1.551605 = 86021/55440
14: 1.590067 = 1145993/720720
15: 1.625781 = 1171733/720720
16: 1.659114 = 1195757/720720
17: 1.690364 = 2436559/1441440
18: 1.719776 = 42142223/24504480
19: 1.747554 = 14274301/8168160
20: 1.773870 = 275295799/155195040
21: 1.798870 = 55835135/31039008
22: 1.822679 = 18858053/10346336
23: 1.845407 = 19093197/10346336
24: 1.867146 = 444316699/237965728
Et si on continue vers l'infini:
29: 1.963586
43: 2.163371
64: 2.364133
95: 2.562910
142: 2.764759
212: 2.965721
317: 3.167270
475: 3.369739
712: 3.572296
1067: 3.774677
1600: 3.977331
2399: 4.179907
3598: 4.382605
5396: 4.585268
8093: 4.787954
12139: 4.990677
18208: 5.193402
27311: 5.396121
40966: 5.598851
61448: 5.801577
92171: 6.004306
138256: 6.207037
207383: 6.409768
311074: 6.612500
466610: 6.815232
699914: 7.017964
1049870: 7.220696
1574804: 7.423428
2362205: 7.626161
3543307: 7.828893
5314960: 8.031626
7972439: 8.234358
11958658: 8.437091
17937986: 8.639823
26906978: 8.842556
40360466: 9.045288
60540698: 9.248021
90811046: 9.450754
136216568: 9.653486
204324851: 9.856219
306487276: 10.058951
459730913: 10.261684
689596369: 10.464416
1034394553: 10.667149
1551591829: 10.869881
2327387742: 11.072614
3491081613: 11.275347
5236622419: 11.478079
7854933628: 11.680812
11782400442: 11.883544
17673600663: 12.086277
26510400994: 12.289009
39765601491: 12.491742
40000000001: 12.494680
Intuitivement, je ne pensais pas que l'on puisse depasser 1.0, mais arriver au dela de 10 est quand meme impressionant.
on voit que si on rajoute 50% de plus de briques, le nombre augmente a peu pres de 0.2.
Je pense que si on tend vers l'infini, cette distance tend egalement vers l'infini, mais exponentiellement plus lentement.
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#17 - 04-03-2011 09:38:23
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3612
- Lieu: 94110
Empilage de briques - Terimnus
#18 - 04-03-2011 14:30:52
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
empilage de briques - terminud
J'ai un peu de temps pour finir de démontrer la question subsidiaire que j'ai donnée sans démonstration.
En reprenant mes notations précédentes, on a:
[TeX]x_{n+1}=\dfrac12+\dfrac1{n+1}{\sum_{i=1}^nx_i}[/latex] (1)
Donc:
[latex]x_{n+1}-x_n=\dfrac{x_n}{n+1}+(\dfrac1{n+1}-\dfrac1{n})\sum_{i=1}^{n-1}x_i=\dfrac{x_n}{n+1}-\dfrac1{n(n+1)}\sum_{i=1}^{n-1}x_i[/TeX]
Finalement:
[TeX]x_{n+1}-x_n=\dfrac1{n(n+1)}(nx_n-\sum_{i=1}^{n-1}x_i)[/TeX]
Cette dernière égalité permet de montrer par récurrence (forte) que la suite [latex](x_n)[/latex] est croissante au sens large. En effet en supposant qu'elle le soit jusqu'au rang n tous les [latex]x_i[/latex] sont plus petits que [latex]x_n[/latex] et donc la différence positive, ce qui le montre jusqu'au rang (n+1). D'autre part la question 1 a permis de le montrer pour les premiers termes.
La suite [latex](x_n)[/latex] est croissante au sens large et à termes positifs donc soit elle est convergente soit elle tend vers l'infini.
Si elle converge et qu'on appelle l sa limite, (1) entraine l'équation [latex]l=\dfrac12+l[/latex] qui n'a pas de solution. Elle ne converge donc pas et donc tend vers l'infini ce qui permet de conclure que l'on peut avancer l'aplomb aussi loin qu'on veut CQFD.
(On peut montrer rigoureusement le point précédent à partir de (1) par encadrement à partir d'un certain rang ou par équivalence mais c'est un peu fastidieux pour tout écrire ici).
J'espère avoir été complet cette fois-ci.
Merci encore.
#19 - 05-03-2011 01:10:09
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Empilaage de briques - Terminus
Je vous invite aussi à chercher ce problème dans les olympiades de mathématiques, je cherche déjà depuis quelques jours, et la solution apporté était bien différente d'après ce dont je me rappelle. 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#20 - 05-03-2011 10:20:58
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3612
- Lieu: 94110
Empilage de rbiques - Terminus
#21 - 22-03-2011 21:20:21
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
empilagr de briques - terminus
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#22 - 22-03-2011 22:51:23
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Empilage de briuqes - Terminus
Ce problème est bien plus ancien que celà 
Les diverses extensions proposées sur P2T sont plus riches mais ils n'est jamais inutile de revoir les bases 
Merci pour le lien .
Vasimolo
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum