Le vase de Klein, par exemple (et tous ses dérivés) ?

Hello!
@Klimrod, @Franck9525: vous avez sauté directement à la question subsidiaire?
Pour vous deux:

Spoiler : [Afficher le message] Une bouteille de Klein ou un ruban de Mobius ce sont des surfaces et non des volumes. Si vous souhaitez en faire des volumes en leur donnant une épaisseur alors le ruban est totalement équivalent a un tore (forme à 1 trou) avec les règles énoncées. La bouteille de klein avec une épaisseur semble avoir clairement un intérieur hermétique (fermé au niveau du croisement) et donc est bien différente d'une forme à N trou, mais une simple boule avec dedans une bulle de vide aurait aussi répondu à la question.

@nodgim:
>> Je n'ai pas très compris comment tu définissais un trou dans un volume. Peux tu
>> préciser ?

Oui je vais préciser, je ne défini pas un trou dans un volume j'ai juste arbitrairement décidé d'appeler "forme à N-trous" le volume résultant de la jonction cote à cote de N tores, comme dans l'image juste dessous avec 3.

@nodgim:
Il y a des règles de déformation autorisée, tu es sur que la forme 6 n'est pas la même qu'une des formes à N trous?

J'ai mis la question en rouge (vu que pas mal de gens ne voient pas la question et ne tentent que de répondre à la subsidiaire) et j'ai ajouté le spoiler pour la forme 6 juste dessous.

@nodgim:
Tente ton opération de pliage en partant simplement de la forme 2trous.
Le début de l'opération est parfaitement faisable car de manière continue en augmentant le contact entre les deux tores tu peux commencer a les superposer pour que du coté charnière ca ressemble à un seul.
Mais de l' autre cote ca forme une sorte de petite bouche (dont les tores formeraient les lèvres) et cette bouche ne disparaitra jamais avec les transformations autorisées.
C'est pour ca que dans l'exemple célèbre de la tasse et de la soucoupe je dis que c' est diffèrent (On ne peut pas passer du tore à la boule) et par conséquent ne pas faire disparaitre la petite bouche évoquée ci dessus.
Tu vois ce que je veux dire?

Si j'ai compris, il s'agit donc d'un ballon de baudruche gonflé qu'on déforme comme on veut ?

Toutes les formes sont des surfaces closes.
Elles se classent donc suivant leur genre.
Le genre représente le nombre de tores accolés auquel la surface est homéomorphe.
Pratiquement, c'est le nombre maximal de coupes que l'on peut pratiquer sans créer plusieurs morceaux.

Dans le cas d'un tore, on ne peut pratiquer qu'une seule coupe sans créer 2 morceaux, dans le cas d'un "bretzel" (2 tores accolés) on ne peut partiquer qu'au plus 2 coupes.

Le genre de la forme 1 est 3.
Le genre de la forme 2 est 2.
Le genre de la forme 3 est 3.
Le genre de la forme 4 est 4.
Le genre de la forme 5 est 5.
Le genre de la forme 6 est 3.

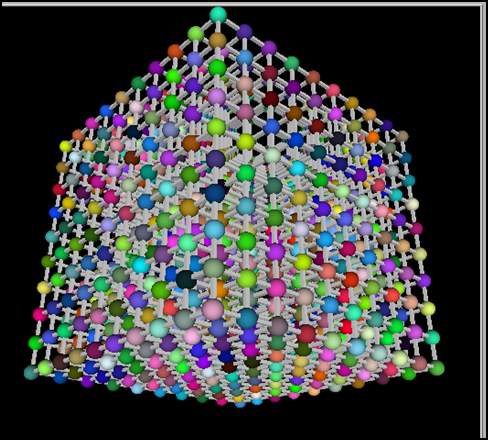
Pour le genre de la forme 7, c'est plus difficile.
Le prend pour N la longueur d'une grande arête. Il y a donc N+1 boules sur une arête (la figure représente donc N=9).
Je ne suis pas sûr mais il me semble que le genre est alors [latex](N+1)^2(3N-1)[/latex]. (Si on prend pour N le nombre de boules on trouve [latex]N^2(3N-4)[/latex]).

Pour la question subsidiaire, une surface de genre 0 convient, par exemple une sphère (épaisse si tu veux faire un volume = boule creuse) ou alors une "surface avec un bord" comme par exemple une sphère (épaisse) avec un trou (d'un côté seulement, pas traversant).

Merci pour cette énigme.

Pour le calcul avec N, j'ai calculé le nombre total d'arêtes [latex]4N(N+1)^2[/latex] et le nombre maximal que l'on doit garder pour ne pas faire 2 morceaux.
Je trouve: [latex](N+1)^3[/latex].
La différence est le nombre de coupes que l'on peut faire sans "scinder" la figure.
(Couper des arêtes ou couper des boules ne change rien).

Pour d'autres surfaces/volumes la boule creuse était un peu tricher, je suis d'accord.
Par contre la boule creuse avec un trou d'un coté me semble radicalement différente (surface avec un bord).
La bouteille de Klein répond au problème mais en dimension 4.
Ou alors il faut chercher vers la surface de Boy mais ce n'est pas simple non plus.

D'ailleurs il faut chercher une surface avec un bord sinon elles sont toutes homéomorphe à un certain nombre de tores accolés.

Peut-être un plan avec un trou (plan projectif)?

@rivas: Voir PM, sinon je crois que je ne trouve pas pareil pour la grille, je vérifierais les calculs ce soir.

@nodgim: Je ne comprend pas trop ce que tu quantifies mais je remarque que tu quantifies la même chose pour Spoiler : [Afficher le message] la forme à 3-trous (3 tores accolés) et la forme 6, ce qui veut dire que tu considères les deux formes comme étant les mêmes? Si oui c'est juste, pour les autres reformule ta conclusion "machin et machin sont les même" etc... 

Bon ba fiasco cette énigme moi qui pensait que faire de la pâte a modelé mentalement ca plairait! il aurait sans doute valu une bonne vidéo exemple.
Solution ajoutée dans le post original.

@Franky1103:
1) Dans mon probleme je ne considère que des volumes, je ne parle jamais de surface. Une bouteille de Klein c'est une surface donc c'est hors sujet, si tu considère le volume induit par la surface d'une bouteille de Klein en lui inculquant une épaisseur, ce volume définit clairement un espace interne hermétique qui ne peut pas disparaitre par déformation et donc ce n'est pas un N-tore collé. (qui dans le probleme sont des volumes plein sans creux interne).

2) Ta question c'est exactement la question subsidiaire de mon énigme, elle ne a donc la même réponse , n'importe quel volume avec un creux quelque part dedans mais surtout ce qu'on appelle les nœud le plus simple étant donné en exemple. (cherche "prime knot" sur google image pour en voir une palanquée)

3) donc pareil qu'en 2, il n'est pas équivalent à un N tore, il est certainement la représentation 3d la plus simple de lui même.

Ps: Ce n'était pas si abstrait comme question ^^ exemple totalement équivalent au transformations qu'il fallait tenter de voir dans cette enigme:
http://www.youtube.com/watch?v=S5fPwE7GQOA

Voila voila.