Pour les gourmands, en revoilà 6 de plus !

Faux, ce n'est effectivement pas bijectif mais :

10001 allumera toutes les lampes pour un tableau de 2 15 18 ou 23 lignes sauf erreur.

01010 allumera toutes les lampes pour un tableau de 6 14 15 ou 23 lignes...

Quel que soit le nombre de ligne je trouve de une à 32 solutions pour attaquer la première ligne et remplir le tableau à la fin.

D'ailleurs c'est très curieux : Avec un tableau de 5 colonnes et 23 lignes, si on applique la méthode, j'ai bien l'impression que le tableau sera rempli quelle que soit la combinaison choisie en ligne 1 .

gwen27 a écrit:

Faux, ce n'est effectivement pas bijectif mais :

10001 allumera toutes les lampes pour un tableau de 2 15 18 ou 23 lignes sauf erreur.

01010 allumera toutes les lampes pour un tableau de 6 14 15 ou 23 lignes...

Quel que soit le nombre de ligne je trouve de une à 32 solutions pour attaquer la première ligne et remplir le tableau à la fin.

D'ailleurs c'est très curieux : Avec un tableau de 5 colonnes et 23 lignes, si on applique la méthode, j'ai bien l'impression que le tableau sera rempli quelle que soit la combinaison choisie en ligne 1 .

Oui Gwen: l'analyse de l'éclairement d'une pièce d'une ligne se fait sur 2 lignes, ce que j'avais omis de faire. En conséquence, une situation de départ peut aboutir sur une situation gagnante, mais avec un nombre de lignes fixe modulo quelque chose.
C'est compliqué à démontrer que ça marche toujours....

Grace à l'observation de Gwen, je suis parvenu à lister toutes les solutions pour les petites grilles carrées, et les résultats sont assez étranges :

Pour des carrés de côté x, il y a y solutions différentes (aux rotations et symétries près) :
x -> y
1->1
2->1
3->1
4->5
5->1
6->1
7->1
8->1
9-> une petite centaine !!!
10->1
Ensuite les essais commencent à prendre beaucoup de temps...

Et voici pour les 4xn :

Pour revenir sur l'exemple 3x3 traité par gwen, la matrice
[TeX] M=\begin{bmatrix}
1&1&0&1&0&0&0&0&0 \endline
1&1&1&0&1&0&0&0&0 \endline
0&1&1&0&0&1&0&0&0 \endline
1&0&0&1&1&0&1&0&0 \endline
0&1&0&1&1&1&0&1&0 \endline
0&0&1&0&1&1&0&0&1 \endline
0&0&0&1&0&0&1&1&0 \endline
0&0&0&0&1&0&1&1&1 \endline
0&0&0&0&0&1&0&1&1 \end{bmatrix}[/TeX]
est inversible dans [latex]\mathbb{Z}/2\mathbb{Z}[/latex] et un logiciel nous calcule
[TeX] M^{-1}=\begin{bmatrix}
1&0&1&0&0&1&1&1&0 \endline
0&0&0&0&1&0&1&1&1 \endline
1&0&1&1&0&0&0&1&1 \endline
0&0&1&0&1&1&0&0&1 \endline
0&1&0&1&1&1&0&1&0 \endline
1&0&0&1&1&0&1&0&0 \endline
1&1&0&0&0&1&1&0&1 \endline
1&1&1&0&1&0&0&0&0 \endline
0&1&1&1&0&0&1&0&1 \end{bmatrix}[/TeX]
On peut donc obtenir n'importe quelle configuration de lumière, et d'une façon unique. En particulier il y a une unique façon d'allumer toutes les lumières :
[TeX] M^{-1} .\begin{bmatrix}
1 \endline
1 \endline
1 \endline
1 \endline
1 \endline
1 \endline
1 \endline
1 \endline
1 \end{bmatrix} = \begin{bmatrix}
1 \endline
0 \endline
1 \endline
0 \endline
1 \endline
0 \endline
1 \endline
0 \endline
1 \end{bmatrix}[/TeX]
ce qui correspond à la solution

#O#
O#O
#O#

Pour d'autres dimensions que 3x3, il se peut que la matrice ne soit pas inversible et l'on aura alors plus de solutions, toujours une puissance de 2.

Je ne connais rien aux matrices mais elles sont toutes drôlement similaires... De là à penser que ce qui est valable pour une l'est pour les autres.

111-
11-1
1-11
-111

11-1-----
111-1----
-11--1---
1--11-1--
-1-111-1-
--1-11--1
---1--11-
----1-111
-----1-11

11--1-----------
111--1----------
-111--1---------
--11---1--------
1---11--1-------
-1--111--1------
--1--111--1-----
---1--11---1----
----1---11--1---
-----1--111--1--
------1--111--1-
-------1--11---1
--------1---11--
---------1--111-
----------1--111
-----------1--11

Pour 17 de côté, il va falloir quelqu'un qui connait le sujet, pas moi en tout cas

titoufred a écrit:

Pour d'autres dimensions que 3x3, il se peut que la matrice ne soit pas inversible et l'on aura alors plus de solutions, toujours une puissance de 2.

J'avais lu "on n' aura plus de solution" au lieu de "on en aura +"

D'où l'insistance inutile du dernier post

@Masab : Tu es sûr de tes résultats, je suis presque sûr qu'il n'y a qu'une solution pour un carré de 5, toutes sont des rotations de la même... (de même pour le carré de 4, où je ne distingue que 5 formes distinctes)

Je résume et complète mes messages précédents pour les rectangles de hauteur m : je donne les motifs se répétant à l'infini fournissant toutes les solutions pour les rectangles mxn, aux symétries près. Pour cela il faut couper la frise en 2 endroits : on commence après une rangée de O et l'on finit avant une autre rangée de O.

m=1 : 1 motif



m=2 : 2 motifs



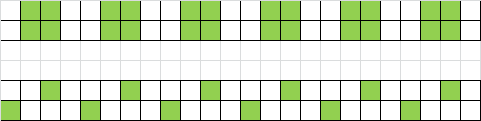
motif 1 : n = 4k, 4k+2 ou 4k+3
motif 2 : n = 2k+1 (4k+1 ou 4k+3)

m=3 : 3 motifs



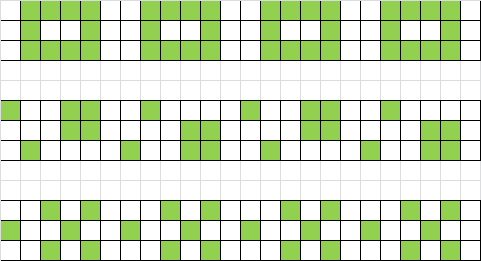
motif 1 : n = 6k, 6k+4 ou 6k+5
motif 2 : n = 3k+2 (6k+2 ou 6k+5)
motif 3 : n = 2k+1 (6k+1, 6k+3 ou 6k+5)

m=4 : 5 motifs



motif 1 : n = 5k, 5k+3 ou 5k+4
motifs 2, 3 et 5 : n = 5k+4
motif 4 : n = 5k+1, 5k+2 ou 5k+4

m=5 : 5 motifs



motif 1 : n = 24k, 24k+6, 24k+7, 24k+8, 24k+14, 24k+15, 24k+16, 24k+22 ou 24k+23
motifs 2 et 3 : n = 12k+3, 12k+7 ou 12k+11 (24k+3, 24k+7, 24k+11, 24k+15, 24k+19 ou 24k+23)
motif 4 : n = 24k+2, 24k+4, 24k+7, 24k+10, 24k+12, 24k+15, 24k+18, 24k+20 ou 24k+23
motif 5 : n = 24k+1, 24k+5, 24k+7, 24k+9, 24k+13, 24k+15, 24k+17, 24k+21 ou 24k+23

Cela confirme les résultats de golgot. Mais je vois pas comment étendre les motifs pour d'autres dimensions...

Merci Titou !

Pour 6xn (zoomable):

On suppose que l'on a un rectangle (p,q). J'ai indiqué dans mon 1er message que résoudre le problème revient à résoudre un système linéaire de [latex]p\,q[/latex] équations à [latex]p\,q[/latex] inconnues, à coefficients dans le corps [latex]\{0,1\}[/latex]  (on a donc [latex]1+1=0[/latex]).
Il en résulte que s'il existe au moins une solution, alors le nombre des solutions est une puissance de 2 (JE NE DIS PAS : le nombre de solutions à rotation ou symétrie axiale près).

Pour résoudre un tel système, j'ai utilisé la méthode de Gauss.
Autrement dit j'ai fait des opérations élémentaires successives sur les équations du système ; une opération élémentaire consiste ici à ajouter à une équation d'autres équations.

Lorsqu'il y a une unique solution (là aussi je ne dis pas à rotation ou symétrie axiale près), alors cette solution est de façon évidente invariante par rotation ou symétrie axiale. Donc si l'on colorie en vert les cases des interrupteurs à ouvrir, on obtient de belles configurations.

Voici le pdf des solutions uniques pour les carrés de côté [latex]1,2,3,6,7,8,10,12,13,15,18,20[/latex].

C'est booooooooooo ! C'est un papillon, on est d'accord ?

Tu l'obtiens comment ton dessin ? Et toi golgot ?
J'en ai marre de faire des trucs tout moche...

golgot, pour les rectangles 7xn, je n'ai trouvé que 27 motifs (avec un programme). T'en aurais pas 2 identiques par hasard ?