 |
#1 - 16-04-2013 16:13:07
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Allumer la maaison
Une maison rectangulaire possède différentes pièces disposées comme sur un quadrillage. Dans chaque pièce, il y a une ampoule et un interrupteur. L'interrupteur situé dans une pièce commande non seulement l'ampoule de la pièce, mais également les ampoules des pièces voisines.
Au départ, toutes les ampoules sont éteintes. Le but est de toutes les allumer.
Voici un exemple pour une maison 3x3 :
Au départ, toutes les ampoules sont éteintes (E) :
EEE
EEE
EEE
On appuie l'interrupteur en haut à gauche, cela allume trois ampoules (A) :
AAE
AEE
EEE
Puis, sur l'interrupteur de la pièce centrale, cela allume trois ampoules et en éteint deux :
AEE
EAA
EAE
Puis en haut à droite :
AAA
EAE
EAE
Puis en bas à gauche :
AAA
AAE
AEE
Puis en bas à droite :
AAA
AAA
AAA
C'est gagné !
On peut résumer cela en cochant les interrupteurs actionnés :
XOX
OXO
XOX
Comment vous y prendriez-vous sur des maisons ayant d'autres dimensions ?
Tous les exemples sont les bienvenus !
NB : Je n'ai pas la moindre idée de comment faire pour d'autres dimensions. Je sais juste que c'est toujours possible.
#2 - 16-04-2013 18:47:33
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
allumer la maiqon
Bonsoir Titoufred
Je pensais avoir déjà posé le problème mais ce n'est pas le cas , je laisse donc chercher ceux qui ne connaissent pas 
Vasimolo
#3 - 16-04-2013 19:22:37
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
Allumer la maiosn
Si Vasimolo pensait avoir déjà posté le problème, doit y avoir un truc avec la couleur des cases d'un échiquier dans la réponse 
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#4 - 16-04-2013 19:43:29
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Allumer la mison
Ou une indigeste histoire de gâteau 
Vasimolo
#5 - 16-04-2013 21:43:47
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Allumer lla maison
Ok. J'ai retrouvé le sujet : EDF ça se complique
Bon, du coup, je modifie mon message initial. Il va falloir essayer de trouver concrètement comment faire !
#6 - 16-04-2013 23:06:21
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
allumee la maison
Moi je suis de la vieille école , je sais que c'est possible alors je laisse faire les jeunes et je me repose 
Mais en temps de crise il n'est pas inintéressant d'économiser les manipulations . On peut aussi supposer qu'initialement toutes les ampoules sont allumées et avec une manipulation par minute tenter de limiter la dépense énergétique avant l'extinction des feux 
Vasimolo
#7 - 17-04-2013 09:12:26
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,193E+3
Allumer l maison
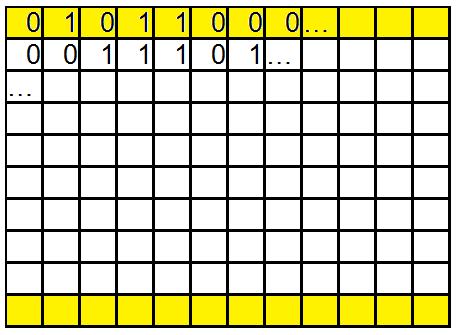
Je pense qu'on a 2^n manières différentes de cliquer sur la rangée de cases du haut. Si on les reporte de ligne en ligne, pour allumer toutes les lampes de la ligne précédente, on se retrouve avec 2^n combinaisons différentes sur la dernière ligne.
Certaines d'entre elles allument forcément toutes les lampes de cette ligne.
#8 - 17-04-2013 18:20:20
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Allumre la maison
Et pour la 3ème ligne Gwen ? N'oublie pas que si touche un bouton de la 3ème ligne, tu agis sur l'allumage des pièces de la seconde ligne.
#9 - 17-04-2013 19:20:56
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,193E+3
Allumr la maison
La seconde ligne n'est pas obligatoirement allumée. Elle sert à allumer la première et donc , on prend les cases sous celles qui restent éteinte dans la première ligne.
De la même façon, la troisième ligne aura pour but d'allumer la seconde.
Exemple : je choisis au pif de jouer en première ligne sur 010110001110 (pour garder cette image. )
La seconde ligne est donc forcée (rouge) , puis la troisième (bleu) .... jusqu'à la dixième. J'ai 2^n combinaisons de départ qui vont en forcer 2^n à l'arrivée.

#10 - 18-04-2013 10:48:57
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
zllumer la maison
gwen, il y a plusieurs problèmes dans ton raisonnement
1) Pourquoi le processus serait-il "injectif", ie 2 combinaisons différentes (d'interrupteurs) en première ligne donneraient 2 combinaisons différentes (d'interrupteurs) en dernière ligne ? En fait, ce n'est pas le cas.
2) La dernière ligne d'interrupteurs ne définit pas à elle seule la dernière ligne de lumières.
En fait, il faudrait remplacer dans ton raisonnement, pour la dernière ligne, combinaison d'interrupteurs, par combinaison de lumières. Mais dans ce cas-là non plus, il n'y a aucune raison non plus que ce soit injectif.
#11 - 18-04-2013 14:29:12
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Allumr la maison
Pour ce qui est de la forme concrète des solutions, je commence (modestement mais surement) par les rectangles de dimensions nx1 :
1x1 : X
2x1 : XO
3x1 : OXO
4x1 : XOOX
5x1 : OXOOX
6x1 : OXOOXO
qu'on généralise facilement à :
(3k+1)x1 : X OOX ... OOX
(3k+2)x1 : OX OOX ... OOX
(3k+3)x1 : OX OOX ... OOX O
#12 - 18-04-2013 16:02:19
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
allumzr la maison
On suppose que l'on a un rectangle [latex](p,q)[/latex].
Il faut en fait raisonner sur l'espace vectoriel [latex](\mathbb{Z}/2\mathbb{Z})^{p\,q}[/latex] sur le corps [latex]\mathbb{Z}/2\mathbb{Z} [/latex] des entiers modulo 2. Les [latex]p\,q[/latex] configurations obtenues en fermant un interrupteur (lorsque toutes les lampes sont éteintes) forment un système de vecteurs (ce n'est pas toujours une base).
On est donc amené à chercher si la configuration "toutes les lampes sont allumées" appartient au sous-espace vectoriel engendré par les vecteurs de ce système ; si l'on explicite dans la base canonique, on est amené à résoudre un système linéaire de [latex]p\,q[/latex] équations à [latex]p\,q[/latex] inconnues.
S'il existe au moins une solution, alors le nombre de solutions est une puissance de 2.
#13 - 18-04-2013 18:14:18
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Allume la maison
J'ai la même réserve que titoufred vis à vis de la démarche de Gwen: la bijection entre le code des boutons manoeuvrés et le code des lumières resultant reste à prouver. Mais c'est tout de même un beau raisonnement.
#14 - 18-04-2013 18:44:18
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Allumer l amaison
Je sais qu'il n'y a pas là de raisonnement, mais voici des solutions pour les premiers carrés, qui me laissent perplexe... :

#15 - 18-04-2013 19:24:51
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
allumer la mzison
Bravo golgot !
Dur dur de voir un point commun pour l'instant...
J'essaye pour ma part les rectangles 2xn...
#16 - 18-04-2013 19:39:02
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
allumrr la maison
Pour le point commun, on remarque déjà que la diagonale des matrices est soit toujours 1 soit toujours 0 et qu'il y a une symétrie axiale selon la diagonale quant il y a que des 1 et une symétrie centrale obtenue par quatre rotations de [latex]\frac{\pi}{4}[/latex] à chaque fois quant il y a que des 0. Il n'y a plus qu'à essayer les deux méthodes pour les nombres de 7 à 20 par exemple.
Sachant que pour la matrice de diagonale avec que des 1 il suffit de faire que la moitié du tableau et avec celle avec que des 0 un quart de tableau suffit. 
Je n'ai pas le temps de m'y plonger mais c'est peut-être une piste à développer...
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#17 - 18-04-2013 19:45:21
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,193E+3
alluler la maison
titoufred a écrit:1) Pourquoi le processus serait-il "injectif", ie 2 combinaisons différentes (d'interrupteurs) en première ligne donneraient 2 combinaisons différentes (d'interrupteurs) en dernière ligne ? En fait, ce n'est pas le cas.
.
Je trouve cette affirmation un peu rapide... Tu dis : en fait, ce n'est pas le cas mais je doute que tu ais un contre-exemple sous la main.
On va raisonner sur une seule ligne OK ?
Je pense que deux combinaisons d'interrupteurs donnent obligatoirement 2 combinaisons de lumières différentes. Si j'arrive à prouver ça, on peut reporter le raisonnement de ligne en ligne , non ? Ca revient donc à prouver que sur une seule ligne, on peut obtenir n'importe quelle combinaison de lumières.
Ca par contre je n'arrive pas à le prouver même si je n'ai pas encore trouvé de contre exemple
#18 - 18-04-2013 19:49:58
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
allumrr la maison
Voici ce que j'ai trouvé pour les maisons 2xn :
2x2 :
XX
XX
2x3 :
OOX
XOO
ou
OXX
OXX
2x4 :
OXXO
OXXO
2x5 :
OOXOO
XOOOX
Qu'on généralise à :
2x(4k+1) :
O OXOO ... OXOO
X OOOX ... OOOX
2x(4k+2) :
XX OOXX ... OOXX
XX OOXX ... OOXX
2x(4k+3) :
XOO OXOO ... OXOO
OOX OOOX ... OOOX
ou
OXX OOXX ... OOXX
OXX OOXX ... OOXX
2x4k :
OXXO ... OXXO
OXXO ... OXXO
#19 - 18-04-2013 20:03:59
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Allumer la maiso
gwen27 a écrit:titoufred a écrit:1) Pourquoi le processus serait-il "injectif", ie 2 combinaisons différentes (d'interrupteurs) en première ligne donneraient 2 combinaisons différentes (d'interrupteurs) en dernière ligne ? En fait, ce n'est pas le cas.
.
Je trouve cette affirmation un peu rapide... Tu dis : en fait, ce n'est pas le cas mais je doute que tu ais un contre-exemple sous la main.
En voici un :
XO
OO
et
OX
OO
gwen27 a écrit:On va raisonner sur une seule ligne OK ?
Je pense que deux combinaisons d'interrupteurs donnent obligatoirement 2 combinaisons de lumières différentes. Si j'arrive à prouver ça, on peut reporter le raisonnement de ligne en ligne , non ? Ca revient donc à prouver que sur une seule ligne, on peut obtenir n'importe quelle combinaison de lumières.
Ca par contre je n'arrive pas à le prouver même si je n'ai pas encore trouvé de contre exemple
Contre-exemple :
O
X
et
X
O
#20 - 18-04-2013 20:18:17
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,193E+3
lAlumer la maison
Je confirme que tu n'as pas compris ce que je veux dire.
Dans ton contre-exemple 1 la seconde ligne amène bien des combinaisons différentes.
Dans ton second contre exemple, tu ne choisis pas les même cases en ligne 1 donc invalide.
En plus le cas de dimension 2 est celui qui amène le plus de discussions car il combine les 2 exceptions des bords, rusé personnage ! A partir de la dimension 3 tu as le même en réserve ?
#21 - 18-04-2013 21:08:49
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Allumer la maion
gwen27 a écrit:Je pense qu'on a 2^n manières différentes de cliquer sur la rangée de cases du haut. Si on les reporte de ligne en ligne, pour allumer toutes les lampes de la ligne précédente, on se retrouve avec 2^n combinaisons différentes sur la dernière ligne.
Certaines d'entre elles allument forcément toutes les lampes de cette ligne.
Gwen, peux-tu expliquer ce dont tu parles en détails ?
Qu'appelles-tu une combinaison sur la dernière ligne ? C'est bien une combinaison d'interrupteurs ?
Peux-tu donner un exemple pour expliquer ce que tu affirmes ?
#22 - 18-04-2013 22:05:51
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,193E+3
Allumeer la maison
Bon , je vais (encore une fois) essayer d'être clair...
En ligne 1 je peux choisir 2^n combinaisons QUI S'EXCLUENT mutuellement.
Un exemple 4x4 :

En ligne 2 , je me vois donc dans l'obligation de choisir 2^n combinaisons (leurs opposés) QUI S'EXCLUENT AUSSI
Cela implique en ligne 3 de retrouver l'opposé de la ligne 2.
Et donc 2^n combinaisons QUI S'EXCLUENT ENCORE
De fil en aiguille, on retrouve 2^n combinaisons en ligne 4 , ce qui oblige à en trouver une valable, SI UNE COMBINAISON PERMET D'ALLUMER TOUTES LES CASES D'UNE LIGNE
#23 - 18-04-2013 22:17:09
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Allumer la maiison
Ok gwen. Je pensais que tu essayais de démontrer qu'il y avait une solution.
En fait, tu expliques une façon de trouver une solution sachant qu'il y en a une.
#24 - 18-04-2013 22:33:48
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,193E+3
Allumer la maion
Oui , ( sans lire d'ironie dans ton propos  ) mais je n'arrive pas à prouver la condition initiale qui prouverait qu'elle existe. Remplir une ligne avec la combinaison de son choix. ) mais je n'arrive pas à prouver la condition initiale qui prouverait qu'elle existe. Remplir une ligne avec la combinaison de son choix.
Je prouve juste que k combinaisons différentes sur la ligne 1 donnent k combinaisons différentes en dernière ligne et que si on prouve que une combinaison permet de compléter une ligne, c'est gagné car k= 2^n en ligne 1 . Mais cela n'exclue pas que plusieurs combinaisons soient valables, ça dit juste qu'il y en a au moins une.
#25 - 19-04-2013 00:39:28
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
allumee la maison
Coucou !
Bon, voici de nouveaux petit dessins très joli mais qui ne font pas beaucoup avancer. Le chiffre en bas à gauche indique la taille du côté du carré (image zoomable).
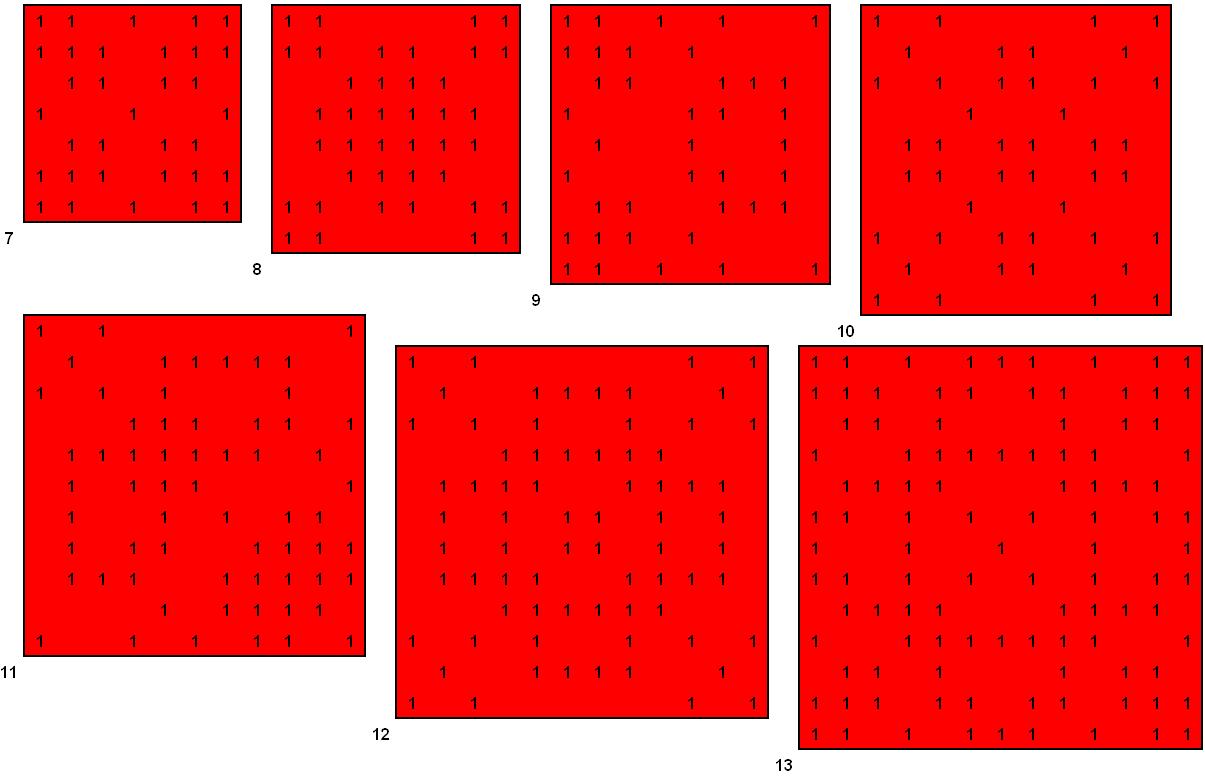
En voulant raisonner sur des tailles pas trop grandes, j'ai hélas trouvé d'autres solutions pour le 9, mais certaines sans aucune symétrie ou rotation !

Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum












