Bonsoir,

nodgim a écrit:

un triangle rectangle isocèle dont le coté à l'angle droit aura pour longueur 1.

Est-ce le côté adjacent ou opposé à l'angle droit ? J'ai supposé que c'était le côté adjacent.
J'ai fait un calcul approché, en testant différentes ouvertures. Si je ne me suis pas trompé :

Volume maximal         = 0.068960
Hauteur d'eau          = 0.626400
Rapport des diagonales = 1.909416

Je pense avoir trouvé au moins une erreur dans mon calcul, et vais revoir tout ça.

Ajouté :
Deuxième proposition

Volume maximal         = 0.065600
Hauteur d'eau          = 0.640388
Rapport des diagonales = 2.083824

@ Enigmatus: là maintenant, j'ai la même chose que toi. Bravo ! As tu une formulation en nombres algébriques ?

@ Ebichu: y a de ça, mais tu as dû faire une erreur de manip quelque part, ce n'est pas le bon résultat. Ton nombre algébrique est cousin du bon, mais...

C'est en effet un problème plutôt piquant, au début je ne savais pas trop comment m'y prendre....

En réalité, ce n'est pas d'une vieille enveloppe qu'est venue l'inspiration, mais de la découpe d'une boîte alimentaire.

C'est bizarre, j'ai vérifié mes calculs, j'ai même fait une figure sur Géospace pour vérifier, je ne vois pas d'erreur.

As-tu noté que je n'avais pas donné ce que tu demandais, mais la taille de la petite diagonale ?

Pour la hauteur d'eau dans la configuration optimale, je trouve [latex]\sqrt{\frac{9+\sqrt{17}}{32}}[/latex] soit environ 0,640388.



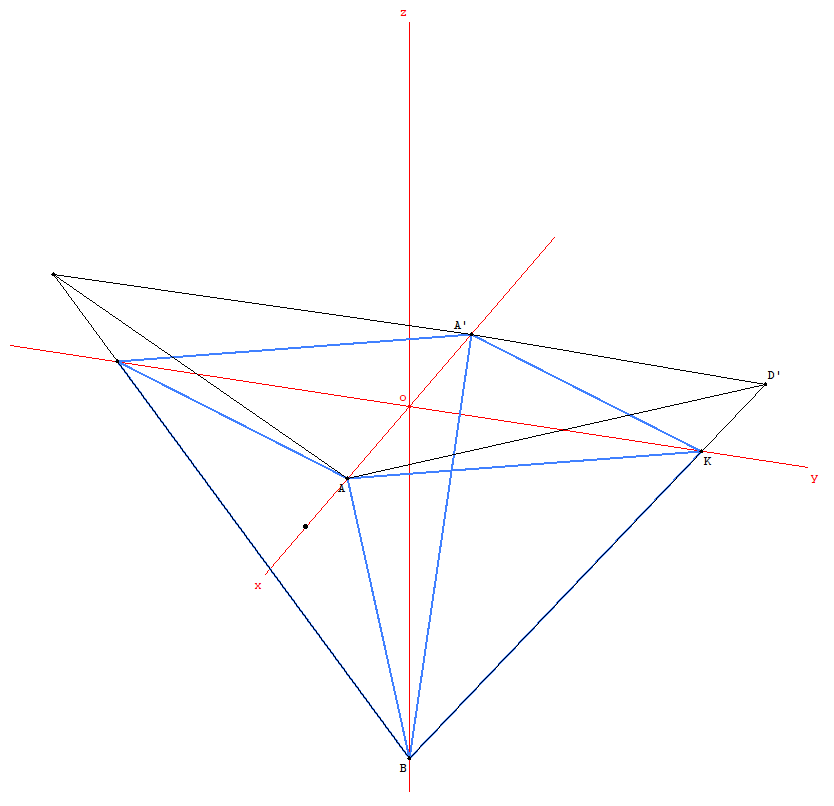
Pour résoudre, j'ai posé L=la petite diagonale (AA' sur la figure).

Dans le repère, j'ai calculé les coordonnées de B(0;0;-racine(2-L²)/2), de D'(0;racine((1-L²)/(2-L²));L²/2racine(2-L²)), puis de K(0;racine((2-L²)(1-L²))/2;0).

J'en déduis que le volume vaut L(2-L²)racine(1-L²)/12.

Or maximiser V, c'est comme maximiser (12V)² soit L²(2-L²)²(1-L²)=-L⁸+5L⁶-8L⁴+4L².

On dérive, on obtient -2L(4L⁶-15L⁴+16L²-4). On pose X=L², il faut trouver les racines de 4X³-15X²+16X-4, et c'est ainsi que vient L=[latex]\sqrt{\frac{7-\sqrt{17}}{8}}[/latex].

Pardon Ebichu, c'est effectivement bon, je n'avais pas calculé la taille de la petite diagonale, et avais lu trop vite ta réponse.

C'est donc bien la bonne hauteur d'eau que tu as donnée, bravo. Cette expression est simplifiable.

Et le rapport des diagonales ?

Question subsidiaire: que vaut le produit des hauteurs des diagonales ?

NB: je suis  passé par une formule qui donne V en fonction de la hauteur d'eau h, puis bien sûr par une dérivée.

100 % OK Ebichu !

Soient A l’angle d’ouverture de l’enveloppe, variant de 0 (enveloppe fermée formant le triangle rectangle initiale) à pi/2 (enveloppe fermée formant un carré) et B celle dans l’autre sens, variant de pi/2 (enveloppe fermée formant le triangle rectangle initiale) à 0 (enveloppe fermée formant un carré).
Soient a et b les deux demi-diagonales du losange minimal (défini par les deux sommets inférieurs) et h la hauteur d’eau.
On aura: a = sin(A/2).V2/2, et: b = h.tan(B/2), avec: h = cos(A/2).V2/2
=> b = tan(B/2).cos(A/2).V2/2
En écrivant que l’arête vaut V2/2 quelle que soit l’angle d’ouverture, on trouve:
sin²(A/2) + 2.sin²(B/2) + [cos(A/2)–V2.cos(B/2)]² = 1
=> cos(A/2).cos(B/2) = V2/2
Le volume vaut: Vol = 2V2.a.b.h/3
=> Vol = sin(A/2).cos²(A/2).tan(B/2).V2/6
Or: tan(B/2) = V[1/cos²(B/2)–1] = V[2.cos²(A/2)–1] = Vcos(A)
D’où: Vol(A) = sin(A/2).cos²(A/2).Vcos(A).V2/6
En posant: X = cos²(A/2), on aura: V(X) = X.[(1-X).(2X²-1)]^(1/2).V2/6
Comme entre 0 et pi/2, la fonction: X = cos²(A/2) est strictement monotone, je peux passer à l'optimisation de X.
Je dérive: V’(X) = – (8X²-9X+2) / [18.(1-X).(2X²-1)]^(1/2)
Dans l’intervalle concerné: V’(X) s’annule pour: X = (9+V17)/16
On a donc: cos²(A/2) = (9+V17)/16, et par conséquence: h = V2.V(9+V17)/8, qui peut se simplifier en: h = (1+V17)/8 = env. 0,6404
Pour le rapport des diagonales, je trouve (mais je n’arrive pas à simplifier le double signe racine): b/a = tan(B/2) / tan(A/2)
b/a = V[(11+3.V17)/8] = env. 1,709

Edit: Erreurs de calcul corrigées.

Je viens de voir que je suis parti d'une longueur 1 pour l'hypoténuse (et non pour le côté à l'angle droit): ça m'apprendra à lire les énoncés correctement. Dans ce cas, je dois multiplier ma hauteur par V2: h = (1+V17)/8 = env. 0,6404
Quand j'aurai plus de temps ce soir, je vais remettre mes calculs au propre avec aussi le rapport des diagonales.

@ Francky: c'est correct maintenant, bravo à toi !
La méthode que tu as employée, en passant par les formules trigonométriques, est différente de celle d'Ebichu ( qui est passé par des coordonnées spatiales) et de la mienne ( qui m'en suis tenu à Pythagore et Thalès ).

@ Enigmatus: tu as donné la formule du carré de la hauteur d'eau. Ce qui est fort, c'est que cette formule semble chez toi sortir d'un algorithme......

Très jolie solution d'Ebichu , et illustrée en plus

Vasimolo

Pour corriger mes calculs, j'ai directement modifié mon post #14 initial.

Ce sont les diagonales du plan d'eau. Voulais tu celles en 3D ? A moins que l'erreur ne viennent pas de là !