 |
#1 - 31-10-2017 07:56:48
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
siite de multiples
Bonjour @ tous,
Cette suite d'entiers strictement croissante commence à 1 et finit à n et chaque entier de la suite (sauf le 1) est un multiple du précédent.
Combien comptez vous de suites distinctes pour aller de 1 à 360 ?
Comptez bien (ça se fait à la main)
Question subsidiaire (je n'ai pas la réponse) : existe t'il un nombre égal au nombre de ses suites ?
#2 - 31-10-2017 10:25:57
- Bastidol
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 152
Suite e multiples
Bonjour,
La dernière valeur de la suite doit elle être égale à 360 ou peut elle être inférieure ou égale ?
Dans le dernier cas le multiple est il toujours le même ?
@+
#3 - 31-10-2017 10:43:03
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
siite de multiples
Bon, j'ai trouvé un nombre égal au cardinal de ses suites !
@Batistol: je ne comprends très bien ta question, aussi je donne un exemple:
Pour arriver à 10, on identifie ces suites :
1 10
1 2 10
1 5 10
Soit 3 suites. Qu'on note ou pas le 10 ne change rien, toutefois c'est plus clair en le notant.
J'ai corrigé l'énoncé, c'était peut être le mot " intermédiaire " qui pouvait prêter à confusion.
#4 - 31-10-2017 12:13:11
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
Suite de multples
Il y a 604 suites de 1 à 360.
Le nombre 48 est égal au nombre de ses suites.
#5 - 31-10-2017 13:20:30
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Suite de multiple
Masab, c'est bien ça, bravo.
Fait à la main ?
#6 - 31-10-2017 15:12:29
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
Sute de multiples
On note ns(n) le nombre de suites associées à l'entier n.
Diviseurs de 360 : 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180, 360
On a
[TeX]ns(n) = 1 + \sum_k ns(k)[/TeX]
la sommation étant pour k diviseur de n différent de 1 et de n.
On a de proche en proche
ns(2) = 1
ns(3) = 1
ns(4) = 2
ns(5) = 1
ns(6) = 3
ns(8) = 4
ns(9) = 2
ns(10) = 3
ns(12) = 8
ns(15) = 3
ns(18) = 8
ns(20) = 8
ns(24) = 20
ns(30) = 13
ns(36) = 26
ns(40) = 20
ns(45) = 8
ns(60) = 44
ns(72) = 76
ns(90) = 44
ns(120) = 132
ns(180) = 176
ns(360) = 604
#7 - 31-10-2017 16:44:07
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
suite de multuples
Hello
Comme résultat pour 360, j'ai 604.
Un exemple de nombre qui se référence lui-même: 48
(Mais aussi 1280 et quelques autres encore)
En gros, f(n) = sum(f(i), i|n), avec f(n) = f(1) = 1 pour n premier.
Accessoirement
- f(p^n) = 2^(n-1) pour p premier
- pour une décomposition en facteurs premiers n = prod(p_i^alpha_i), f ne dépend que des alpha_i (autrement dit, f(6 = 2x3) = f(143 = 13 x 11) = 3; f(48 = 2^4 x 3) = f(6875 = 5^4 x 11) = 48)
#8 - 31-10-2017 17:59:04
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
suitz de multiples
C'est OK pour vous deux, Masab et Scarta, bravo à vous.
@ Scarta: bien pour le second nombre "parfait" !
#9 - 31-10-2017 20:20:25
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
suite se multiples
Voici comment je vois les choses :
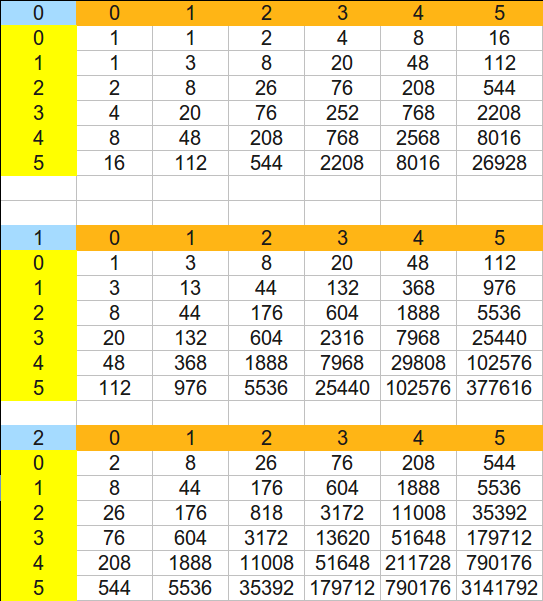
Pour faire le décompte des suites pour un entier n (ici, 360), on détermine le nombre f de facteurs premiers distincts de n (ici, 3), et on fait un tableau à f entrées.
Ici, 360 = 2^3 * 3^2 * 5^1, donc je fais un tableau à triple entrée (en trois dimensions). Pour le remplir, la case (0,0,0) est initialisée à 1, puis pour remplir une case (a,b,c), je fais la somme de tous les nombres dans le pavé dont deux sommets opposés sont (0,0,0) et (a,b,c) (sauf la case (a,b,c) elle-même.
Par exemple, j'obtiens 818 en faisant (1+1+2+1+3+8+2+8+26) + (1+3+8+3+13+44+8+44+176) + (2+8+26+8+44+176+26+176). Ce qui me donne que le nombre de suites pour tout nombre de la forme p1².p2².p3² où p1, p2, p3 sont premiers vaut 818.
Pour la question de départ, je vais chercher dans mon tableau la case de coordonnées (3,2,1) et je trouve 604.
Sinon, pour la question subsidiaire, on peut regarder les cases du tableau et chercher quelles cases contiennent un nombre dont les puissances de la décomposition en facteurs premiers correspond aux coordonnées de la case : c'est le cas de 48 = 2^4 * 3^1 dans la case (4,1), mais aussi de 29808 = 2^4 * 3^4 * 23^1 dans la case (4,4,1).
#10 - 31-10-2017 20:42:29
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
suite de multioles
D'ailleurs, dans le même genre que 48, en se concentrant sur les nombres du type p1^k * p2^1, on peut constater que tous les nombres du type 2^(2p-2) * p (avec p premier) répondent à la question subsidiaire.
Par exemple, c'est le cas ensuite de 2^8 * 5 = 1280, 2^12 * 7 = 28672...
#11 - 31-10-2017 22:44:33
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
#12 - 01-11-2017 08:28:40
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
suite de multipmes
@ Ebichu : OK pour le nombre cherché et OK pour la question subsidiaire. Cependant, ton message 10 n'est pas tout à fait correct, en particulier sur la formulation de l'infinité de ces nombres égaux au cardinal de leurs suites. Tu n'es pas loin, il faut juste ajuster et si possible prouver.
@ Scarta: vu. Sauras tu prouver qu'il existe une infinité de ces nombres "parfaits" (égaux au cardinal de leurs suites) ?
#13 - 01-11-2017 09:42:14
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
Suite de multtiples
Nombres parfaits inférieurs à 10 millions :
[TeX]48=2^4\times 3[/TeX]
[TeX]1280=2^8\times 5[/TeX]
[TeX]2496=2^6\times 3\times 13[/TeX]
[TeX]28672=2^{12}\times 7[/TeX]
[TeX]29808=2^4\times 3^4\times 23[/TeX]
[TeX]454656=2^{12}\times 3\times 37[/TeX]
[TeX]2342912=2^{14}\times 11\times 13[/TeX]
#14 - 01-11-2017 11:11:28
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
quite de multiples
Nombres parfaits compris entre 10 millions et 100 millions :
[TeX]11534336 = 2^{20}\times 11[/TeX]
[TeX]57409536 = 2^{18}\times 3\times 73[/TeX]
#15 - 01-11-2017 11:27:45
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Suite de muliples
Pour la formulation, je ne vois pas de problème, hormis que j'aurais dû préciser "avec p premier >2" ?
La démonstration, ce n'est pas une grosse affaire : il suffit de constater par récurrence que pour un nombre du type [latex]n=p^k[/latex], le nombre de suites est [latex]2^{k-1}[/latex], puis que pour un nombre du type [latex]n=p_1^k.p_2^1[/latex], le nombre de suites est [latex]2^{k-1}.(k+2)[/latex].
Ainsi, pour un nombre du type [latex]n=2^{2p-2}.p[/latex], le nombre de suites est [latex]2^{2p-3}.2p[/latex] soit le même nombre.
#16 - 01-11-2017 15:20:47
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
syite de multiples
C'est tout à fait correct, Ebichu, J'avais fait une mauvaise lecture car j'avais en tête une suite différente qui ressemblait à la tienne. ça en fait 2 maintenant.
@ Masab: il existe bien d'autres nombres "parfaits" (dans le contexte de ce problème, les nombres parfaits étant autre chose) et même une infinité !
#17 - 01-11-2017 15:34:32
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Suite de mltiples
@ Ebichu: en fait, on a trouvé le même ensemble, c'est de mon coté qu'une nuance m'avait échappée, c'est corrigé maintenant.
Bravo à toi.
#18 - 01-11-2017 16:49:17
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
Suite e multiples
Mais existe-t-il d'autres nombres "parfaits" inférieurs à 100 millions ?
#19 - 01-11-2017 16:54:08
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
Suite de multtiples
La suite des nombres "parfaits" est donnée dans le lien
https://oeis.org/A163272
#20 - 01-11-2017 18:06:20
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
suite de multipleq
Pour un nombre p^n.q, p et q premiers distincts, le résultat est (n+2).2^(n-1)
Pour un premier q impair, on pose n= 2q-2
Et donc 2^n.q sera une valeur "parfaite"
3 donne 48, 5 donne 1280, 7 donne 28672, etc...
A noter que ce ne sont pas les seuls. Mais ça prouve déjà l'infinité
#21 - 01-11-2017 19:16:10
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Suite de muliples
@ Scarta: c'est bien ça, bravo à toi.
@ Masab: Le jeu sur ce site n'est pas d'aller chercher la solution sur internet. A titre d'info, ça ne manque pas d'intérêt, mais ce n'est pas le but principal.
#22 - 02-11-2017 08:40:52
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
#23 - 02-11-2017 10:03:52
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
suite de lultiples
nodgim : @ Masab: Le jeu sur ce site n'est pas d'aller chercher la solution sur internet.
Je ne suis pas du tout allé chercher la solution sur un autre site !
A l'aide d'un programme informatique de ma conception, j'ai trouvé la suite :
48, 1280, 2496, 28672, 29808, 454656, 2342912, 11534336, 57409536
En mettant cette suite dans google, je me suis aperçu avec étonnement qu'il s'agissait d'une suite connue. C'était juste une remarque ; je n'ai pas vu indiqué sur ce lien que la suite des nombres "parfaits" était infinie.
#24 - 02-11-2017 11:35:11
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Suite de multipples
@ Masab : OK. Tu vois, OEIS ne dit pas tout !
@ Halloduda: Ben, non. J'ai horreur de passer derrière les autres, quel intérêt ?
Je pourrais citer la source d'inspiration, mais elle est assez éloignée de ce problème. Maintenant, il est vrai que ça devient difficile de trouver une énigme qui n'existe pas quelque part sur Internet, et je ne peux pas passer mon temps à vérifier le risque de plagiat involontaire !
#25 - 02-11-2017 14:55:18
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
Suuite de multiples
Pour [latex]p[/latex] nombre premier, on peut démontrer que le nombre de suites associées à [latex]n=p^r[/latex] est [latex]2^{r-1}[/latex] ([latex]r\geq 1[/latex]).
|
 |

 Accueil
Accueil
 Forum
Forum







