 |
#1 - 14-09-2022 13:01:08
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
Intition 3 : suite et fin
Considérons une suite définie par une relation de récurrence - autrement dit, une suite de nombres, dont on peut calculer le suivant à chaque fois en regardant les précédents.
Exemple 1: U(0) = 1, U(n+1) = 2*U(n)
La suite U correspond à 1, 2, 4, 8, ... bref les puissances de 2
Exemple 2: U(0) = U(1) = 1, U(n+2) = U(n+1) + U(n)
La suite correspond à 1, 1, 2, 3, 5, 8, 13, 21, 34, 45, ... la suite de Fibonacci
Certaines suites peuvent devenir constantes parfois.
Par exemple, U(0) = un entier quelconque, et U(n+1) = [U(n)/2]
(comme celle-ci : 123 -> 61 -> 30 -> 15 -> 7 -> 3 -> 1 -> 0 -> 0 -> 0 ...)
Et on peut, de manière automatisée, décider pour n'importe quelle suite si elle a une "fin" (si elle devient constante).
C'est vrai ou c'est faux ?
#2 - 14-09-2022 17:24:14
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Intuition 3 : suiet et fin
Bonjour
Je sais qu'il existe des variantes de la suite de Syracuse dont il a été prouvé qu'elles étaient indécidables ( les axiomes usuels de l'arithmétiques ne permettent pas de trancher ) . On ne sait d'ailleurs toujours pas si c'est le cas de la suite de Syracuse .
De tels résultats peuvent paraître contre-intuitifs car pour des valeurs initiales données on se dit :"ça converge ou pas" . Cette logique de comptoir est tout à fait valable pour des valeurs données des paramètres mais ne fonctionne plus quand il s'agît de montrer que la propriété est vraie pour tous les choix des valeurs initiales .
J'ai aussi entendu parlé des séquences de Goodstein qui convergeraient vers "0" sans qu'on puisse le prouver avec l'axiomatique de base de l'arithmétique .
En fait je ne sais pas si je réponds vraiment à la question posée 
Vasimolo
#3 - 14-09-2022 17:45:25
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
Intuition 3 : suite et fiin
Quasiment  En fait ça peut même se prouver (c'est assez rigolo, la démonstration n'est pas très dure et tu peux la trouver, en anglais, dans un article publié il y a 86 ans. Spoiler : [Afficher le message] Article qui a d'ailleurs été à la base de quelque chose de beaucoup plus large que ce qu'il souhaitait prouver à la base ) En fait ça peut même se prouver (c'est assez rigolo, la démonstration n'est pas très dure et tu peux la trouver, en anglais, dans un article publié il y a 86 ans. Spoiler : [Afficher le message] Article qui a d'ailleurs été à la base de quelque chose de beaucoup plus large que ce qu'il souhaitait prouver à la base )
#4 - 14-09-2022 22:46:38
- Migou
- Expert de Prise2Tete
- Enigmes résolues : 17
- Messages : 893
- Lieu: Ville 2/N près 2*i
Intuitionn 3 : suite et fin
Je répondrai faux : on ne peut pas automatiser, et la suite de syracuse donne un contre exemple.
Pour être tout à fait rigoureux, je définis une famille de suites Sk, inspirées de la celèbre conjecture, et définies par :
soit Sk la suite définie par
U(0) = k, avec k un nombre entier positif non nul.
si U(n) = 1, U(n+1)=1
U(n+1)=U(n)/2 si U(n) est pair
U(n+1)=U(n)*3 + 1 si U(n) est impair
On sait que les mathématicien ne sont pas parvenus à prouver la convergence de cette fonction, puisque cela équivaut de de façon triviale à prouver la conjecture de syracuse.
On pense que toutes les suites de syracuse convergent, mais on ne sait pas le prouver.
On pourrait vouloir tester toutes les valeurs jusqu'à atteindre la convergence, mais seulement, on n'a aucune garantie d'y arriver dans un temps réalisable par une machine. En effet, en choisissant bien U(0), le nombre d'étapes pour atteindre la convergence peut être aussi long que l'on veut. (prouvable par récurrence : pour tout nombre d'étapes N, il existe une suite Sk dont le nombre d'étapes est N+1)
#5 - 15-09-2022 09:43:17
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
intuition 3 : suite et gin
@Migou : désolé, mais pas d'accord...
On pense que blablabla mais on ne sait pas le prouver
Peut-être n'a-t-on pas encore trouvé la bonne démonstration.
D'ailleurs tu avances un argument, et c'est marrant le chef pâtissier avance exactement l'inverse.
Et attention : prouver la convergence de manière automatisée ne veut pas forcément dire "parcourir toute la suite jusqu'à la fin". Une démonstration mathématique n'est qu'une succession d'étapes logiques et ça peut, formellement, être automatisé. Je n'ai pas besoin de parcourir toute la suite des 2^n pour savoir qu'elle ne converge pas. La preuve :
* Soit N un entier quelconque
* Soit E l'ensemble des entiers strictement supérieurs à log2(N)
* E est un ensemble d'entiers non-vides --> il admet un plus petit élément, noté n
* On a U(n) = 2^n > N
* Pour tout k>0, U(n+k) = U(n) * 2^k > U(n) > N
==> Pour tout entier N, il existe un certain rang n à partir duquel la suite U est toujours supérieure
==> La suite diverge
C'est une construction mécanique à partir d'axiomes.
#6 - 15-09-2022 09:58:10
- aunryz
- Elite de Prise2Tete
- Enigmes résolues : 17
- Messages : 1419
- Lieu: Nicastro / Tronville
intuitoon 3 : suite et fin
J'ai passé des nuits à en rêver.
J'aimerais tant voir Syracuse !
___
Donc c'est faux
Lélio Lacaille - Du fagot des Nombreux
#7 - 15-09-2022 14:35:17
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
intuotion 3 : suite et fin
Vu que tout le monde en parle dans sa réponse : il n'a pas été prouvé que Syracuse converge, il n'a pas été prouvé que Syracuse diverge, et il n'a pas non plus été prouvé que c'était indémontrable, si ? (ou alors j'ai raté une info capitale)
Et donc, peut-être qu'on peut le démontrer de manière automatisée (dans le sens "ça n'est pas impossible de le faire"), bien qu'on n’arrive pas aujourd'hui à formaliser cette démonstration. Un certain théorème a bien attendu 400 ans et l'arrivée des courbes elliptiques avant d'être prouvé, il n'était pas considéré comme indémontrable entre-temps (indémontrable dans le sens "je peux prouver qu'il n'existe pas de démonstration")
Quoi qu'il en soit, je ne parle pas de convergence mais de constance. Je peux très facilement prouver que la suite de Syracuse ne devient jamais constante. La preuve tient en deux lignes.
Soit k une valeur de départ de la duite de Syracuse, soit U_k(n) un terme quelconque de cette suite.
--- Soit U(n) est pair, dans ce cas U_k(n+1) = U_k(n) / 2, donc U_k(n+1) ≠ U_k(n) (sauf si c'est 0, on peut ajouter quelques lignes pour prouver que si k≠0, alors U_k(n) aussi)
--- Soit U(n) est impair, dans ce cas U_k(n+1) = U_k(n) * 3 + 1, donc U_k(n+1) ≠ U_k(n) (sauf si c'est -1/2, mais ça n'est pas acceptable)
--> Conclusion : il n'y a pas deux termes consécutifs égaux. La suite ne peut donc pas devenir constante.
A la rigueur, la suite S3 qui regarde 3 termes plus loin sur Syracuse peut convenir. Mais encore une fois, prouvez-moi que c'est indémontrable (ou tentez autre chose)
#8 - 15-09-2022 18:28:58
- aunryz
- Elite de Prise2Tete
- Enigmes résolues : 17
- Messages : 1419
- Lieu: Nicastro / Tronville
Intuition 3 : suite e fin
Merci des précisions et du détours vers Syracuse.
Juste une question
comment obtiens-tu la suite
"123 -> 61 -> 30 -> 15 -> 7 -> 3 -> 1 -> 0 -> 0 -> 0 "
?
Merci d'avance
Lélio Lacaille - Du fagot des Nombreux
#9 - 15-09-2022 19:35:41
- Migou
- Expert de Prise2Tete
- Enigmes résolues : 17
- Messages : 893
- Lieu: Ville 2/N près 2*i
intuition 3 : suite et fon
Hélas Scarta, ce matin je me disaisbien que l'argument de la suite de Syracuse était un peu faible.
Justement parce que si jamais un jour on parvient à démontrer sa convergence pour tout Uo, le contre exemple - choisi par tout le monde ici apparemment - tombe à l'eau.
Bon ben, reste à chercher.
#10 - 15-09-2022 23:00:04
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
Intuition 3 : suit eet fin
@Aunryz: come indiqué 
U(n+1) = [U(n)/2] -- c'est à dire la moitié, arrondie à l'inférieur
C'est juste un exemple de suite qui devient constante
#11 - 16-09-2022 00:46:06
- aunryz
- Elite de Prise2Tete
- Enigmes résolues : 17
- Messages : 1419
- Lieu: Nicastro / Tronville
Intuiton 3 : suite et fin
Tu écris
[@Aunryz: comme indiqué
U(n+1) = [U(n)/2] -- c'est à dire la moitié, arrondie à l'inférieur
C'est juste un exemple de suite qui devient constante]
C'est justement la notation qui m'a interrogé
j'ignorais que les crochets [] avaient le sens de l'arrondi inférieur (partie entière)
(J'en étais resté à E() accessible au clavier)
Et je voulais aussi savoir ce que tu acceptais comme opérations (et notamment pour la partie entière) dans les suites sur lesquelles on peut se pencher.
Lélio Lacaille - Du fagot des Nombreux
#12 - 16-09-2022 02:14:16
- Zindy
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 107
intuitiin 3 : suite et fin
J'aurais tendance à dire que c'est vrai.
Si on définit U(n+1) à partir de U(n), on peut écrite U(n+1) = f(U(n))
Connaissant la fonction f(x) on peut graphiquement déterminer les éléments suiccessifs de la suite, et ça permet de voir si on diverge / converge mais surtout, il suffit de voir si la fonction admet un point fixe (je ne sais pas si ça s'appelle comme ça) tel que f(x) = x, pour cela, il faut que la courbe de f(x) coupe la droite y=x
A l'opposé, si la courbe f(x) ne coupe jamais la droite y=x, on n'a pas de point tel que f(x) = x, donc on n'aura jamais U(n+1) = U(n) puisque f(U(n)) = U(n+1).
Ci-dessous une illustration de comment progresser dans la suite à partir de la courbe f(x).
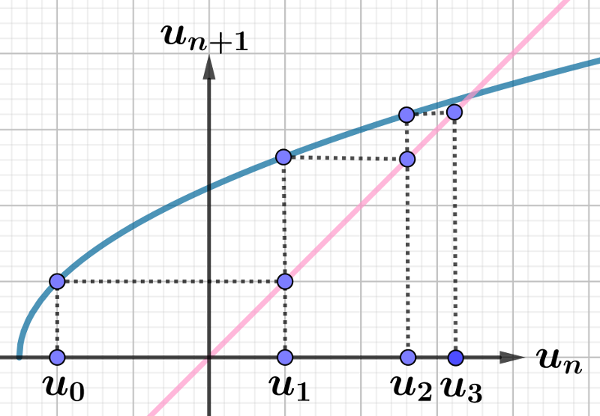
Dans le cas de cette courbe, il existe un point f(x) = x donc on pourrait avoir une suite contstante, mais je me demande si on ne pourrait pas n'avoir qu'une suite convergente qui tend vers la solution de f(x) = x sans jamais l'atteindre ?
#13 - 16-09-2022 10:24:22
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
Intuition 3 : suite e fin
@Aunryz : c'est une bonne remarque. Disons que toutes les opérations mathématiques et logiques sont valides.
Sinon, c'est vrai qu'on peut rentrer dans certains paradoxes. Par exemple en utilisant le paradoxe de Berry ou le paradoxe de Richard.
U(n)=le plus petit nombre qu'on ne peut décrire avec n caractères.
Vu que chaque terme n'est pas vraiment calculable, ça va être rock'n roll de trouver si ça converge 
@Zindy : on peut oui tendre vers une limite sans jamais l'atteindre.
Par exemple, U(0)=1, U(n+1) = U(n)/2 tend vers 0 mais ne l’atteint jamais.
Ta fonction f serait alors f(x)=x/2, point fixe pour x=0, mais ça ne t'aide pas.
Tout ce que tu peux dire, c'est que si la suite atteint cette valeur, alors elle deviendra constante. Mais le peut-elle ?
Dans le cas f(x) = x/2, tu peut facilement vérifier que l'antécédent de 0 est aussi 0, et donc si U(n)=0 pour un certain n, alors U(n-1) aussi etc, jusqu'à U(0) = 0 alors qu'il vaut 1.
On vient donc de démontrer de manière formelle que cette suite ne devient pas constante.
#14 - 19-09-2022 00:44:57
- aunryz
- Elite de Prise2Tete
- Enigmes résolues : 17
- Messages : 1419
- Lieu: Nicastro / Tronville
Intuition 3 : suit eet fin
Je crois lire dans ton message le conseil de
s'appuyer sur ce qui est indémontrable actuellement
merci.
Je m'y essaie
Soit la suite U de couples définie par
U(n) = ((a(n);(b(n)) nième couple de nombres premiers jumeaux
(On a ainsi définit aussi a(n) et b(n))
Soit la suite V définie par
V(n) = plus grande valeur de la suite a(n), pour n inférieur ou égal à n
Il est possible, à cette heure, que l'on ne puisse pas démontrer de manière automatisée, si V(n) devient constante.
Si cette nuit, quelqu'un a démontré la conjecture de Polignac, il faudra que je cherche autre chose 
Lélio Lacaille - Du fagot des Nombreux
#15 - 19-09-2022 07:45:31
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
intuition 3 : suiye et fin
Attention : personne n’a démontré qu’elle n’était pas démontrable. Donc jusqu’à preuve du contraire elle l’est.
Par « résultat non démontrable », on entend habituellement « résultat dont on a prouvé que s’il est vrai, alors la théorie mathématique dans laquelle on est reste cohérente, et idem s’il était faux ».
Exemple : les 5 axiomes d’Euclide sont 5, parce qu’on a fini par prouver (après 2000 ans) qu’aucun ne peut être prouvé par les 4 autres. On peut considérer qu’un axiome est faux, et on obtiendra une géométrie tout à fait valide (quoique assez abstraite)
#16 - 19-09-2022 12:47:10
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
intuiyion 3 : suite et fin
Alors : pour faire court, la réponse est non, il n'existe pas de manière automatisée de savoir si une suite "s'arrête".
La démonstration (enfin une des démonstrations) est, comme je le mentionnais dans un des posts, "pas très dure et [on peut] la trouver, en anglais, dans un article publié il y a 86 ans." Plus exactement, ici : https://www.cs.virginia.edu/~robins/Tur … r_1936.pdf
La vision "Turing a inventé les ordinateurs grace à ses machines", c'est pas faux, mais c'est assez raccourci comme vision. A la base, Turing se penchait sur un problème à la mode à l'époque , le Entscheidungsproblem (ou Problème de la décision), autrement dit, peut-on décider qu'un résultat est vrai ou faux.
Et pour ça, il a introduit un concept, la "machine", c'est-à-dire un opérateur, même humain, qui réalise des opérations pour lesquelles il est préprogrammé, via un "état", des "rubans", etc... mais à aucun moment il ne parle de construire une telle machine, c'était plus une construction de l'esprit pour résoudre son problème.
Par contre, Turing a été, dans le même papier, père de deux résultats majeurs.
Tout d'abord, la machine universelle (qu'on appelle aujourd'hui MTU, Machine de Turing Universelle, ou UTM en anglais). Les machines dont parlent Turing ont un programme qui est propre à leur "construction", et c'est tout. Turing a démontré (page 12 du PDF, page 241 dans l'article, et suivantes) qu'il existe une machine "U" capable de lire la description "m" d'une autre machine "M" et de réaliser le même calcul que cette machine "M". Autrement dit, c'est un peu l'ancêtre d'un langage de programmation. Et de ce fait, une machine a une description standard (SD), de nos jours on dirait code source.
Et second résultat, Turing définit aussi (page 4 ou 233) la notion de machines circular et circle-free, les premières qui ne s'arrêtent jamais tandis que les secondes oui. Et là, résultat fondamental pour Turing et son Entscheidungsproblem, il prouve (page 18 ou 247) qu'il n'existe pas de machine M capable de dire si la description standard d'une machine X s'arrête ou pas (circular ou circle free).
En informatique théorique, on dit tout simplement: l'arrêt est indécidable.
Retour sur notre problème : on peut tout à fait considérer une suite de nombre comme étant la description d'une suite d'état d'une machine de Turing. Ou, pour les plus sceptiques, on peut transcrire l'état d'une machine sous forme de nombre, et définir une suite U(n) qui serait l'état de la machine lors de la n-ème étape.
Et comme l'arrêt est indécidable, il n'y a aucun moyen automatique de savoir, pour toutes ces suites, si elles s'arrêtent ou pas. Pour des cas particuliers, oui, mais pas pour tout.
La démonstration de Turing (comme souvent dans les cas de non-décidabilité) introduit un soupçon d'autoréférence. Autrement dit, si on pouvait démontrer l'arrêt d'un programme mécaniquement, on pourrait en faire une machine, qui serait elle-même un programme. On pourrait alors construire un autre programme (basé sur le premier) qui s'arrête d'après notre machine si et seulement si il est supposé ne pas le faire et vice versa (donc c'est absurde). Même raisonnement que Cantor et son livre des réels (d'ailleurs Turing dans son papier appelle ça l'argument de la diagonale, en référence à Cantor)
Si je ne vous ai pas encore perdu, la suite de l'article est encore plus fun. Sachant qu'une machine peut être utilisée pour écrire un réel, MAIS que chaque machine est caractérisée par une définition standard et que ces définitions sont dénombrables, alors on a une correspondance "réel --> entier"
Et donc la conséquence : soit on vient de prouver que les réels sont contenus dans les entiers, soit il y a des nombres "incalculables"
#17 - 19-09-2022 17:08:44
- aunryz
- Elite de Prise2Tete
- Enigmes résolues : 17
- Messages : 1419
- Lieu: Nicastro / Tronville
intuition 3 : suiye et fin
Merci pour la ballade
tu m'as donné l'occasion d'aller voir du côté de ce problème de l'arrêt de Turing
Mais je n'ai pas pensé que cela pouvait être la solution
bêtement je cherchais encore à produire une suite
ce qui m'a donné (je viens de voir que tu as donné ta réponse)
U(1) = produit des 2 premières décimales de pi modulo 26 + 64
U(3) = produit des 2 suivantes …
U(4) = idem
V(0) = Car(U(1)&Car(U(2)& … s’arrête lorsque pour la valeur de n = n0 tel que U(n0) = 64
V(1) = Car(U(n0+1) & Car(U(n0+2) … s’arrête lorsque pour la valeur de n = n1 on a U(n1) = 64
W(0) = 1 si V(0) est sur internet, sinon W(0) = 0
W(n) = 1 si V(N) est sur internet, sinon W(N) = 0
(oui, ... bon (sourire)²)
et ... (un détour par Borges et sa bibliothèque de Babel)
(la bible est ici considérée sans ponctuation)
U(0)= 1ère caractère de la bible
U(1)= 2ème caractère de la bible
U(2)= 3ème caractère de la bible (un espace)
V(n)= place de U(n) dans l’alphabet , si U(O) est un espace alors V(0)=27
W(0)= V(0)
W(n)=nombre obtenu par concaténation des termes de V(0) à V(n)
Z(n) = 1 si W(n) se trouve dans la séquence des décimales de pi), sinon 0
(mais toujours ce problème de "pas démontré que c'est pas démontrable, à savoir pi nombre univers)
[ou
A(n) = 1 si W(n) se trouve dans la séquence des décimales d'UN des termes de la suite B(m) = 1 + 1/2 + 1/3 + ... 1/m ]
_________________________
Tu écris "Et donc la conséquence : soit on vient de prouver que les réels sont contenus dans les entiers, soit il y a des nombres "incalculables"
On frôle ici l'axiome de choix ?
Lélio Lacaille - Du fagot des Nombreux
#18 - 19-09-2022 18:39:11
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Intuition 3 : suite et fni
J'avoue ne pas avoir compris l'objectif de l'énigme ( je n'ai pas lu les références dans la langue de Charles III ) . Si j'ai bien compris tes explications , Turing montre qu'il existe des suites dont on ne peut pas prévoir le comportement à l'infini , j'adhère complètement au résultat , je sais de même ( résultat bien plus fort ) qu'il existe des résultats indécidables dans le modèle arithmétique usuel .
Si la réponse attendue était "il existe de telles suites" , nous l'avons tous plus ou moins dit . Fallait-il le justifier en exhibant des références un peu lourdes ?
Plus concrètement j'ai souvent lu qu'il existait des suites apparentées à celle de Syracuse pour lesquelles on avait prouvé l'indécidabilité du comportement à l'infini . Je serais curieux de connaitre la description de ces suites .
Vasimolo
#19 - 19-09-2022 19:04:00
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
Intuition 3 : suite et fn
« Il existe des résultats indécidables » : on est d’accord.
Mais à mon humble avis, ça n’est pas plus fort que ce que montre Turing (en l’occurrence que l’arrêt est indécidable). « Il en existe » ne prouve pas que « celui-là l’est ».
Note que l’énoncé de Turing n’est pas non plus plus fort que l’énoncé général. C’est différent c’est tout. Comme si on disait « Il existe des entiers naturels » et « 3 est un entier naturel ».
Quant à la « variante » de Syracuse qui est indécidable, en réalité une version « généralisée », Conway a effectivement démontré que ça n’était pas décidable.
La version généralisée dit en gros : suivant une valeur de i modulo n, on va avoir n équations affines d’un terme vers le suivant.
Et pour savoir si on peut démontrer la convergence pour toutes ces suites, quelques soient les règles, … plot twist … Conway a démontré que c’était équivalent justement au problème de l’arrêt ! Donc indécidable.
(D’où ma réflexion sur la démo quand tu as parlé des familles de Conway et la référence faite à Turing derrière).
Edit : j’aurais voulu mettre un lien vers la démonstration de John Conway, j’ai cherché pas mal mais elle est introuvable. Je sais qu’elle est publiée dans un volume disponible à la bibliothèque universitaire du coin (en tout cas il l’était il y a 20 ans que je l’ai lu la 1ere fois). A l’occasion j’irai la scanner.
En gros, quelle que soit une machine de Turing et la valeur qu’on passe en entrée, Conway arrive à sortir une fonction de style Collatz (avec des facteurs différents) donc chaque nombre successif correspond à l’état de la machine étape après étape. Et donc puisque l’arrêt est indécidable pour toutes les machines, il existe au moins une machine qu’ont l’arrêt est indécidable et il existe aussi une fonction de collatz dont la convergence est indécidable.
|
 |

 Accueil
Accueil
 Forum
Forum







