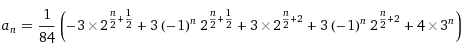|
#1 - 21-02-2011 18:23:06
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3615
- Lieu: 94110
Quelle est la suit e? (Réponse finale).
Quelle est la 15ème valeur de cette suite ?
0, 1, 1, 5, 11, 37, 103, 317, 935, 2821, 8431, 25325, 75911, 227797, ...
(le premier terme étant la valeur 0).
Tous les jours j'ajouterai un indice et un terme supplémentaire à cette suite.
N'hésitez pas à me faire part de vos réflexions ou de vos questions, même si vous n'avez pas réussi à valider la case réponse.
Spoiler : [Afficher le message] Merci à toni77 et à gwen27 pour leur aide involontaire dans la définition de cette énigme.
Spoiler : [Afficher le message] Les différents termes peuvent être trouvés grâce à cette formule :
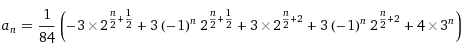
Merci à Memento pour me l'avoir indiquée.
Spoiler : [Afficher le message] ... mais pour ma part je préfère utiliser 2 formules toutes simples, l'une pour les termes pairs, l'autre pour les termes impairs.
Spoiler : [Afficher le message] La case 1 a un certain rapport avec les termes impairs, la case 2 avec les termes pairs (ou bien le contraire, cela dépend d'où on commence la numérotation !).
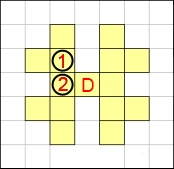
Spoiler : [Afficher le message] La figure précédente illustre l'énigme http://www.prise2tete.fr/forum/viewtopic.php?id=8203 de tony77.
#2 - 21-02-2011 19:25:50
- Memento
- Professionnel de Prise2Tete
- Enigmes résolues : 30
- Messages : 176
quelme est la suite ? (réponse finale).
Pour le 15éme nombre, c'est donc 683263.
J'ai finalement trouvé la formule, il s'agit de:
[TeX]\ u(0)=0
\ u(n) = \left\{
\begin{array}
3*u(n-1)-2^{n/2} & \quad \mbox{si $n$ est pair}\\
3*u(n-1)+2^{(n-1)/2} & \quad \mbox{si $n$ est impair}\\ \end{array} \right. \[/TeX]
Autrement dit:
#3 - 21-02-2011 20:31:33
- guilhem
- Passionné de Prise2Tete
- Enigmes résolues : 27
- Messages : 60
- Lieu: sur Tatouïne, chez Luke
quelle est la suiye ? (réponse finale).
voila l'algo de la suite
... Ok je sort
--------->
#4 - 21-02-2011 20:35:46
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,193E+3
Quelle est la suite ? (Répoonse finale).
Il n'y a pas de quoi ! Il ne me reste plus qu'à comprendre pourquoi ce merci...
#5 - 21-02-2011 22:39:37
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3615
- Lieu: 94110
quelle est la suite ? (eéponse finale).
Bravo à Memento qui a validé le bon résultat ; il ne lui reste plus qu'à expliquer comment ...
#6 - 22-02-2011 03:03:01
- L00ping007
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 2010
- Lieu: Paris
Quelle est la suite ? (Rééponse finale).
693263 !
Chaque nombre est le triple du précédent, auquel on ajoute ou retranche alternativement les puissances de 2 :
0
3x1-2=1
3x1+2=5
3x5-4=11
3x11+4=37
3x37-8=103
3x103+8=317
3x317-16=935
3x935+16=2821
3x2821-32=8431
3x8431+32=25325
3x25325-64=75911
3x75911+64=227797
3x227797-128=683263
Peut-on exprimer les termes en fonction de n ? 
EDIT
Après quelques calculs sur les suites des termes pairs et impairs, grace a la relation de récurrence ci dessus, je trouve :
[TeX]a_{2n}=\frac{3^{2n}-2^n}7
a_{2n+1}=\frac{3^{2n+1}+2^{n+2}}7[/TeX]
Le terme qui nous intéresse est le 15ème, soit [latex]a_{14}[/latex]
#7 - 22-02-2011 10:07:07
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
Quelel est la suite ? (Réponse finale).
0, 1, 1, 5, 11, 37, 103, 317, 935, 2821, ...
Je trouve:
[TeX]u_0=0, u_1=1[/TeX][TeX]u_{2n}=2*u_{2n-1}+3*u_{2n-2}-2^{n-1}[/TeX][TeX]u_{2n+1}=2*u_{2n}+3*u_{2n-1}[/TeX]
Je vérifie:
[TeX]u_2=2*1+3*0-1=1[/latex]: OK
[latex]u_3=2*1+3*1=5[/latex]: OK
[latex]u_4=2*5+3*1-2=11[/latex]: OK
[latex]u_5=2*11+3*5=37[/latex]: OK
[latex]u_6=2*37+3*11-4=103[/latex]: OK
[latex]u_7=2*103+3*37=317[/latex]: OK
[latex]u_8=2*317+3*103-8=935[/latex]: OK
[latex]u_9=2*935+3*317=2821[/latex]: OK
[latex]u_{10}=2*2821+3*935-16=8431[/TeX]
Je propose donc 8431 qui n'est pas validé.
Ma formule valide pourtant 8 termes successifs, est relativement simple.
#8 - 22-02-2011 12:31:48
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3615
- Lieu: 94110
quelle est la suite ? (réponqe finale).
#9 - 22-02-2011 21:59:35
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3615
- Lieu: 94110
Quelle ets la suite ? (Réponse finale).
Re-Bravo à LOOping  qui trouve une 4ème formulation pour la même suite ! qui trouve une 4ème formulation pour la même suite !
J'ai ajouté un indice et un onzième terme à la suite.
#10 - 23-02-2011 09:46:33
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
quemle est la suite ? (réponse finale).
Merci pour ton post Jackv, je n'ai en effet pas vu que l'on cherchait le 15ème terme.
Je continue donc:
[TeX]u_{11}=2*8431+3*2821=25325[/TeX]
[TeX]u_{12}=2*25325+3*8431-32=75911[/TeX]
[TeX]u_{13}=2*75911+3*25325=227797[/TeX]
[TeX]u_{14}=2*227797+3*75911-64=683263[/TeX]
Le 15ème terme est donc 683263, ce qui est validé par la case réponse.
Du coup, j'en profite pour donner une formule (par récurrence) qui fusionne les rang pairs et impairs:
[TeX]u_{n+2}=2*u_{n+1}+3*u_n-(1+(-1)^n)*2^{\dfrac{n}2-1}[/TeX]
C'est assez simple: le dernier terme à un coefficient qui vaut 0 pour les n impairs et 2 pour les n pairs, il suffit donc d'y ajouter la puissance de 2 que l'on désire derrière.
#11 - 23-02-2011 10:05:00
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
Qulle est la suite ? (Réponse finale).
683263
Aucun intérêt quand on a la formule.
#12 - 23-02-2011 11:23:01
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3615
- Lieu: 94110
Quelle est la suiet ? (Réponse finale).
Bravo sans réserve à rivas  qui en profite pour donner une 5ème formulation ! qui en profite pour donner une 5ème formulation !
Et bravo aussi à halloduda  qui trouve la réponse en contournant un peu le problème. qui trouve la réponse en contournant un peu le problème.
J'ai ajouté un nouvel indice et le 12ème terme de la suite.
#13 - 23-02-2011 15:06:44
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,193E+3
Quuelle est la suite ? (Réponse finale).
OK, compris, je trouve :
0, 1, 1, 5, 11, 37, 103, 317, 935, 2821, 8431 , 25325, 75911, 227797, 683263
(tu as du faire une erreur d'un rang dans l'indice) Non mais c'est pas fini d'éditer pendant que je poste !
Pour les rangs pairs: Sn = S(n-1) + 6 S(n-2)
Pour les rangs impairs : Sn = 9 S(n-2) - 2 ^(n/2) Euh un petit bug dans la formule je crois mais c'est l'esprit
#14 - 23-02-2011 19:27:52
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3615
- Lieu: 94110
quelle esr la suite ? (réponse finale).
Bravo aussi à Gwen 
#15 - 24-02-2011 09:54:14
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3615
- Lieu: 94110
quelle est la syite ? (réponse finale).
J'ai ajouté une 13ème valeur et un nouvel indice.
#16 - 25-02-2011 16:01:00
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3615
- Lieu: 94110
Quelle est la suite ? (Réonse finale).
J'ai ajouté le 14ème et dernier terme.
#17 - 25-02-2011 22:53:00
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3615
- Lieu: 94110
Quelle est la suite ? (Réponse fianle).
Cette suite fait référence au nombre de chances pour qu'un pion se déplaçant
sur une grille partielle occupe une position donnée au bout de N déplacements à partir de la case centrale de la grille.
La figure suivante illustre ces chances pour les coups de 1 à 9 : c'est le rapport entre le nombre en rouge et le dénominateur situé sous chaque dessin ; à chaque coup, ce dénominateur est multiplié par 3.
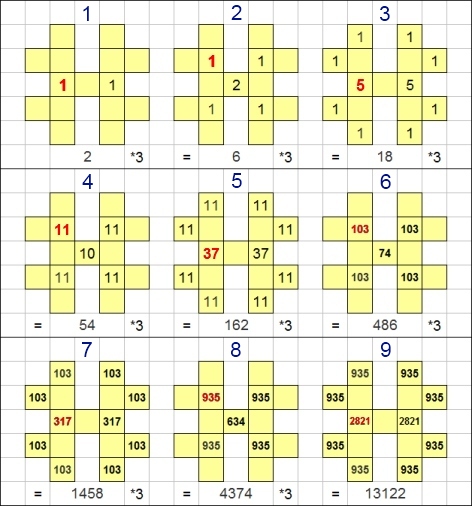
Il est aisé de voir que le numérateur vaut :
- pour un coup pair : [latex]u_n = 6 * u_{n-2} + u_{n-1}[/latex]
- pour un coup impair : [latex]u_n = 3 * u_{n-2} +2 * u_{n-1}[/latex]
Le 15ème terme de la suite (correspondant au numérateur du 14ème déplacement) vaut donc 683263.
Encore un grand bravo à tous ceux qui ont participé et ont réalisé globalement un sans faute, en trouvant presque à chaque fois une manière différente de l'exprimer.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum