 |
#51 - 28-10-2013 10:33:20
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 239
Un cadeau exigeatn
Edit : ma démonstration n'est pas valide (voir les posts suivants), inutile de lire ce post
Il semble que je sois condamné à détaille mes explications à chaque fois 
A l'avenir, essayer de préciser quel point pose problème, ça m'évitera de tout réexpliquer à chaque fois.
Dans ma démonstration par l'absurde, il faut considéré que je prends les cotés dans l'ordre croissant des longueur (ce qui ne change rien), sans me soucier de fermer le polygone avant le 733eme coté. La seule contrainte que doit vérifier le "prépolygone" est qu'un coté doit posséder au plus un autre coté parallèle pour assurer la convexité à la fin.
On peut toujours définir la notion de périmètre pour ces prépolygones convexes comme la somme des |a|+|b| où les (a,b) sont les cotés.
Pour un prépolygone convexe de N cotés quelconques, on peut minimiser son périmètre en réduisant chaque couple (ka,kb) en (a,b) où a est premier avec b, ça légitime le fait de ne considérer que les a premier avec b pour minimiser le périmètre.
Ensuite, toujours pour minimiser le périmètre, on prends les N cotés dans les N premier couples (a,b) rangés par longueur |a|+|b| croissante.
Dans ces conditions pour N=732 cotés, ma liste dans mon premier post (+ leurs 4 ou 8 variations) satisfont à ces conditions de minimalité. Donc le périmètre minimal d'un prépolygone de 732 cotés est bien 4*2993.
Les seul libertés pour choisir ce prépolygone minimal de 732 cotés est le choix des derniers cotés parmis ceux de longueurs 25. On a vite fait de voir que pour que le prépolygone reste encadré dans un carré de 3000 de coté, la seule manière de faire est de choisir ces cotés de longueur 25 de manière à ce qu'on forme un polygone convexe inscrit dans un carré de 2993 de coté.
On ne peut bien entendu pas rajouter un 733eme coté à ce polygone sans sortir du carré 3000.
Mais peut être qu'il existe une solution de 733 cotés valide mais ne respectant pas la stratégie de minimisation du périmètre. Dans ce cas les 732 cotés les plus courts forme un prépolygone non optimal de périmètre forcément > 4x2993.
Le 733eme coté (le plus long) est au moins de longueur 25. Si la longueur ou la largeur du prépolygone était déja de 3000, le 733eme coté devrait être de type (0,x). Cela signifierais qu'un des couples de type (0,1) n'est pas utilisé à cause de la contrainte du maximum de 2 cotés parallèle. Cela décalerait les couples choisis dans la liste en rajoutant au moins 25-1=24 au périmètre minimal de 4x2993 du prépolygone de 732 cotés (il n'y aurait plus que 4 de marge avant 4x3000, pas de quoi caser le 733eme coté).
Donc le 733eme coté rajoute au moins 1 à la largeur et à la hauteur du prépolygone (si on utilise un couple du type (1,x) avec x>=24). Donc le prépolygone doit nécessairement être inclus dans un carré de 2999 de cotés.
Le cotés le plus court du rectangle dans lequel est inscrit le prépolygone est donc supérieur à (2993x4-2999x2)/2, donc au moins de longueur 2988.
Enfin, en rajoutant le 733eme coté à ce prépolygone, une des composantes sera au moins de longueur 13 (avec le couple (12,13)).
2988 + 13 = 3001.
CQFD
Cette fois j'espère que tout est claire 
#52 - 28-10-2013 10:59:36
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,192E+3
Un cadeau eigeant
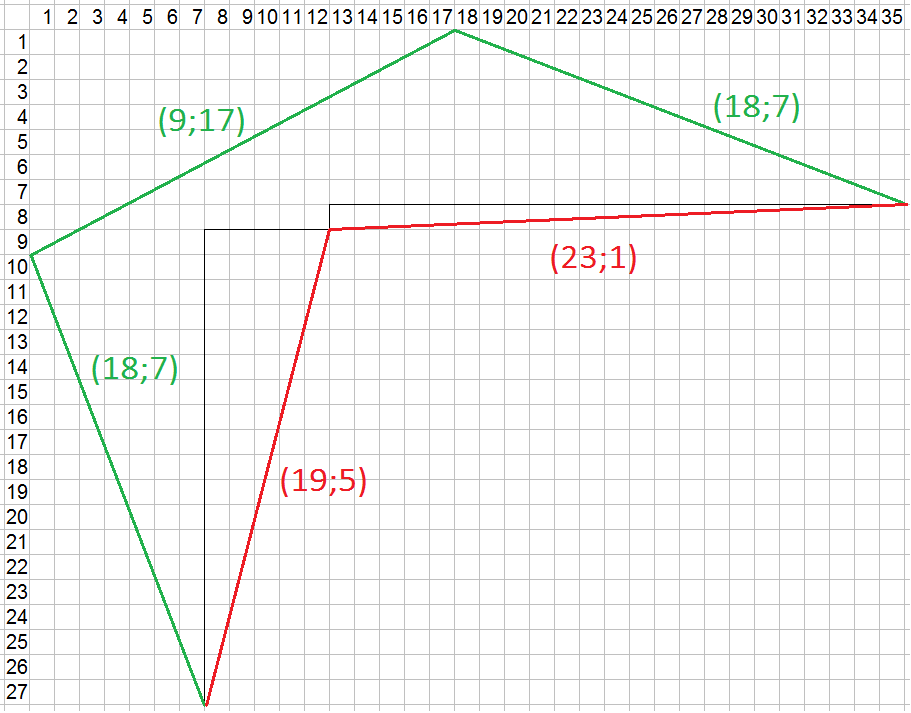
Et que se passe-t-il si dans ton polygone fermé de 732 côtés dans un carré de 2993x2993 , tu remplaces deux vecteurs par 3 vecteurs équivalents mais n'augmentant la largeur que de 7 :
#53 - 28-10-2013 11:13:58
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 239
un cadeau exigrant
Bien vu gwen, je me suis piégé moi même avec mon astuce de prendre des polygones incomplet : en rajoutant le dernier coté, en fait on n'augmente même pas du tout la taille! On ne fait que fermer le polygone.
Le mystère reste entier...
#54 - 28-10-2013 16:06:43
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,192E+3
un cadeau exigzant
Et donc, si on peut le faire une fois, c'est 733 même s'il doit y avoir d'autres solutions.
J'ai bêtement copié tes couples et sommé sous excel dans les 4 cadrans du carré 3000 x3000.
Puis, j'ai rajouté un exemplaire du 2-23 , du 0-1 et du 1-1
Enfin, j'ai fait l'échange du dessin au dessus. On a même une petite marge 
On reste dans le cadre avec 733 côtés. Il resterait juste à classer les côté par tangence pour avoir le polygone dans l'ordre.
#55 - 28-10-2013 17:27:51
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 239
un cafeau exigeant
Quand tu dis que tu rajoute un exemplaire du 0-1 et du 1-1, tu veux dire que tu rallonge un 0-1 en 0-2, et un 1-1 en 2-2 ?
Parce qu'autrement les 8 couples de type 0-1 et 1-1 étaient déjà tous utilisés dans mon premier polygone.
Je rappelle ce que j'avais fais : pour les couple que listé j'en utilisait dans l'ordre 4,4,8,8,8,...8,4. Toutes les variations de signe et permutation abscisse/ordonnée était utilisé sauf pour le dernier couple 2-23 utilisé 4 fois seulement, alors qu'il existe comme pour les autres (excepté 0-1 et 1-1) 8 variations.
#56 - 28-10-2013 17:42:52
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 239
un cadeau exigzant
En fait en faisant directement la transformation de ton dessin, sans rien modifier d'autre ça marche! 
ce qui change par rapport à ma distribution de 732 cotés:
7 couple 1-23 au lieu de 8
7 couple 5-19 au lieu de 8
2 couple 7-18 au lieu de 0
1 couple 9-17 au lieu de 0
Bilan : 2 couple enlevés, 3 rajoutés, périmètre : 4x2993-2x24+2x25+26 = 12000 pile poil, ça rentre pile dans le 3000x3000 comme le montre ton dessin.
Donc bravo même si tu n'as pas vu que tu avais déjà trouvé au post précédent 
#57 - 28-10-2013 18:57:00
- Lise-et-Paris
- Habitué de Prise2Tete
- Enigmes résolues : 0
- Messages : 17
#58 - 28-10-2013 20:05:23
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,192E+3
Un cadeau xigeant
w9Lyl6n a écrit:Donc bravo même si tu n'as pas vu que tu avais déjà trouvé au post précédent 
Je ne savais pas comment faire les calculs, alors j'ai pris tous les couples 8 fois présents en les répartissant selon leur orientation. (BG BD HG HD)
Puis j'ai rajouté à la main ceux qui m'ennuyaient (0-1 , 1-1)
Et j'ai fait les échanges 2 couples 7-18 et
1 couple 9-17 au lieu de 1-23 et 5-19
Mais de là à poster un truc clair, je me suis borné à "l'astuce"
#59 - 28-10-2013 20:25:32
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 239
un cadeau exogeant
Pour clore le sujet, j'ai écris un JavaScript pour vérifier et faire les dessins.
Il y a deux dessins :
1) les vecteurs partant tous du centre de l'image
2) la forme finale à l'échelle 0.3 pixel = 1 point
Le résultat affiché dans la console me dit:
"cotés : 733, périmètre : 11988, largeur : 2997, hauteur : 2997, sommeX : 0, sommeY : 0"
Je m'étais donc un peu trompé (j'avais compté en double (0,1) et (1,1)) mais de toute manière il n'y a pas de quoi rajouter un coté supplémentaire avec une marge de 40 au lieu de 28 pour le périmètre.
Du coup il y a sûrement encore plus de solutions à 733 cotés.
Pour afficher les résultats et dessiner les images :
-pour Chrome Ctrl+Maj+J
-pour Firefox Ctrl+Maj+K
coller le code dans la console et exécuter le en appuyant sur entrée.
Scroller en bas de la page pour voir les images.
Code:var all=[ [1, 2], [1, 3], [1, 4], [2, 3], [1, 5], [1, 6], [2, 5],
[3, 4], [1, 7], [3, 5], [1, 8], [2, 7], [4, 5], [1, 9], [3, 7], [1, 10],
[2, 9], [3, 8], [4, 7], [5, 6], [1, 11], [5, 7], [1, 12], [2, 11],
[3, 10], [4, 9], [5, 8], [6, 7], [1, 13], [3, 11], [5, 9], [1, 14],
[2, 13], [4, 11], [7, 8], [1, 15], [3, 13], [5, 11], [7, 9], [1, 16],
[2, 15], [3, 14], [4, 13], [5, 12], [6, 11], [7, 10], [8, 9], [1, 17],
[5, 13], [7, 11], [1, 18], [2, 17], [3, 16], [4, 15], [5, 14], [6, 13],
[7, 12], [8, 11], [9, 10], [1, 19], [3, 17], [7, 13], [9, 11], [1, 20],
[2, 19], [4, 17], [5, 16], [8, 13], [10, 11], [1, 21], [3, 19], [5, 17],
[7, 15], [9, 13], [1, 22], [2, 21], [3, 20], [4, 19], [5, 18], [6, 17],
[7, 16], [8, 15], [9, 14], [10, 13], [11, 12], [1,23], [5, 19], [7, 17],
[11, 13], [1, 24]],
except=[[5,19],[23,1]],
add=[[-7,18],[17,9],[18,-7], [2, 23],[-2,-23],[23,2],[-23,-2], [0,1],[0,-1],[1,0],[-1,0], [1,1],[-1,-1],[1,-1],[-1,1]],
canvas = document.createElement('canvas'),
g=canvas.getContext('2d'),
sommeX = 0,
sommeY = 0,
W=0,
H=0,
perimetre=0,
cotes = 0,
ratio = 20;
canvas.height=canvas.width=50*ratio;
g.fillStyle = "red";
function line(x,y,w,l){
g.beginPath();
g.strokeWidth=1;
g.moveTo(x*ratio,y*ratio);
g.lineTo((x+w)*ratio,(y+l)*ratio);
g.stroke();
g.beginPath();
g.strokeWidth=0;
g.arc((x+w)*ratio, (y+l)*ratio, 2, 0, Math.PI*2, true);
g.fill();
}
function vect(x,y){
line(25,25,x,y);
cotes++;
sommeX+=x;
sommeY+=y;
if (x>0) W+=x;
if (y>0) H+=y;
perimetre+=Math.abs(x)+Math.abs(y);
}
g.strokeStyle = "#aaaaaa";
for (var i=0; i<50; i++){
line(0,i,50,0);
line(i,0,0,50);
}
var x,y;
for (var v in all) {
x=all[v][0]; y=all[v][1];
add.push([x,y],[-x,-y],[-x,y],[x,-y],[y,x],[-y,-x],[-y,x],[y,-x]);
}
add.sort(function (v,w) {return Math.atan2(v[0],v[1])-Math.atan2(w[0],w[1]);});
g.strokeStyle = "black";
for (var v in add) {
x=add[v][0]; y=add[v][1];
if ((x!=5 || y!=19) && (x!=23 || y!=1))
vect(x, y);
}
document.querySelector('body').appendChild(canvas);
canvas.parentNode.style.textAlign = "center";
ratio = 0.3;
var c2 = document.createElement('canvas');
c2.height=c2.width=3000*ratio;
g = c2.getContext('2d');
g.fillStyle = "red";
g.strokeStyle = "black";
var xx=2999,yy=1508;
for (var v in add) {
x=add[v][0]; y=add[v][1];
if ((x!=5 || y!=19) && (x!=23 || y!=1))
{
g.beginPath();
g.moveTo(xx*ratio,yy*ratio);
xx+=x; yy+=y;
g.strokeWidth=0.5;
g.lineTo(xx*ratio,yy*ratio);
g.stroke();
g.beginPath();
g.strokeWidth=0;
g.arc(xx*ratio, yy*ratio, 1, 0, Math.PI*2, true);
g.fill();
}
}
document.querySelector('body').appendChild(c2);
"cotés : "+cotes
+", périmètre : "+perimetre
+", largeur : "+ W
+", hauteur : "+H
+", sommeX : "+sommeX
+", sommeY : "+sommeY;Enjoy ! 
#60 - 28-10-2013 21:35:33
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
un cadeau zxigeant
Pour ceux qui aiment chercher plus loin 
La longueur maximale d'un polygone convexe inscrit dans un carré de [latex]n\times n[/latex] points est [latex]4(n-1)[/latex] . Le nombre total de vecteurs de longueur inférieure ou égale à [latex]k[/latex] est [latex]4\sum_{i=1}^k\varphi(i)[/latex] pour une longueur totale de [latex]4\sum_{i=1}^ki\varphi(i)[/latex] ( [latex]\varphi[/latex] désignant l'indicatrice d'Euler ) . Après selon la taille du carré on trouve aisément le nombre maximum de côtés que l'on peut espérer .
Dans cet exemple ce maximum est atteint : est-ce toujours le cas ?
Vasimolo
#61 - 01-11-2013 23:37:37
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
U cadeau exigeant
Le nombre maximum de côtés prévus par la grossière majoration Manatthan :

Au moins jusqu'à [latex]n=9[/latex] ce maximum peut être atteint .

après ...
Vasimolo
#62 - 02-11-2013 10:41:15
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
un caseau exigeant
Je vais ajouter quelque chose sur la longueur maximale de 4(n-1) du polygone.
En fait, pour maximiser ses chances, il faut bien entendu occuper le maximum d'espace. Le polygone s'étend donc du haut jusqu'en bas et de gauche à droite, en touchant les bords. Comme de haut en bas il fait un aller retour, et pareil de droite à gauche, on peut dire qu'il traverse 2 fois toutes les lignes et 2 fois toutes les colonnes. Le nombre de cases traversées est donc 4(n-1), auquel il faut toutefois ôter les points qu'il rejoint, c'est à dire justement le nombre de ses cotés (car en passant sur un point, il franchit en même temps une ligne et une colonne).
#63 - 02-11-2013 19:13:06
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
in cadeau exigeant
Bonjour,
12000 ne me semble pas une bonne réponse, en revanche 3000 conviendrait (plus grand polygone plat) !
Plus sérieusement, il faudrait effectivement essayer de trouver une règle générale, à partir d'exemples plus simples...
Pour le moment, je trouve seulement 220 côtés avec une méthode simpliste consistant à avancer selon des diagonales de rectangles de hauteur 1 et de longueur n, n-1, n-2,...,2,1,0 jusqu'à atteindre la moitié de la hauteur soit 1500 : n(n+1)/2=<1500 pour n=54. Avec le côté verticale, cela donne 55 et en reportant sur les 3 autres quadrants, cela fait 55*4=220.
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#64 - 02-11-2013 23:42:31
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Unn cadeau exigeant
fix33 a écrit:Plus sérieusement, il faudrait effectivement essayer de trouver une règle générale, à partir d'exemples plus simples...
N'est-ce pas ce que nous sommes en train de faire ?
Vasimolo
#65 - 02-11-2013 23:55:30
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
in cadeau exigeant
J'ai beaucoup tardé à poster, ce post je l'avais écrit en tout début d'après-midi je crois ! Vous avez vraiment bien mieux bossé que moi ! 
En fait, non c'est parce que je n'ai dû lire que la 1ère page de posts... 
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#66 - 03-11-2013 09:52:29
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,192E+3
U ncadeau exigeant
Vasimolo a écrit:Le nombre maximum de côtés prévus par la grossière majoration Manatthan :
Au moins jusqu'à [latex]n=9[/latex] ce maximum peut être atteint .
après ...
Il peut être atteint et dépassé parfois... pour 34 on obtient théoriquement 37 côtés par exemple.
#67 - 03-11-2013 11:19:39
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
un cadeau exiheant
Ce n'est pas tout à fait ça ce que j'ai dit 
Le périmètre d'un polygone convexe inscrit dans un quadrillage [latex]n\times n[/latex] est inférieur ou égal à [latex]4(n-1)[/latex] . Il y a en tout [latex]4\sum_{i=1}^k\varphi(i)[/latex] côtés possibles de longueur inférieure ou égale à [latex]k[/latex] . On cherche alors le [latex]k[/latex] maximal tel que [latex]4\sum_{i=1}^ki.\varphi(i)\leq4(n-1)[/latex] et on divise la longueur restante sur le périmètre pour voir combien de côtés de longueur [latex]k+1[/latex] on peut encore ajouter . C'est le tableau que j'ai joint au message #61 .
La première faille apparaîtrait pour [latex]n=11[/latex] , à confirmer .
Vasimolo
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum










