Bonjour bonjour
Je ne suis pas vraiment nul en maths, mais là je sèche. Je dois faire un plan d'un pavillon qu'on est allé visiter en Allemagne (à part la bouffe et le temps qui étaient dégeulasses, ça s'est bien passé ) pour nos études d'architecture, et j'ai un problème pour calculer une hauteur.Je vous présente la piste que j'ai prise, et si vous pouvez me dire si c'est bon ou pas...
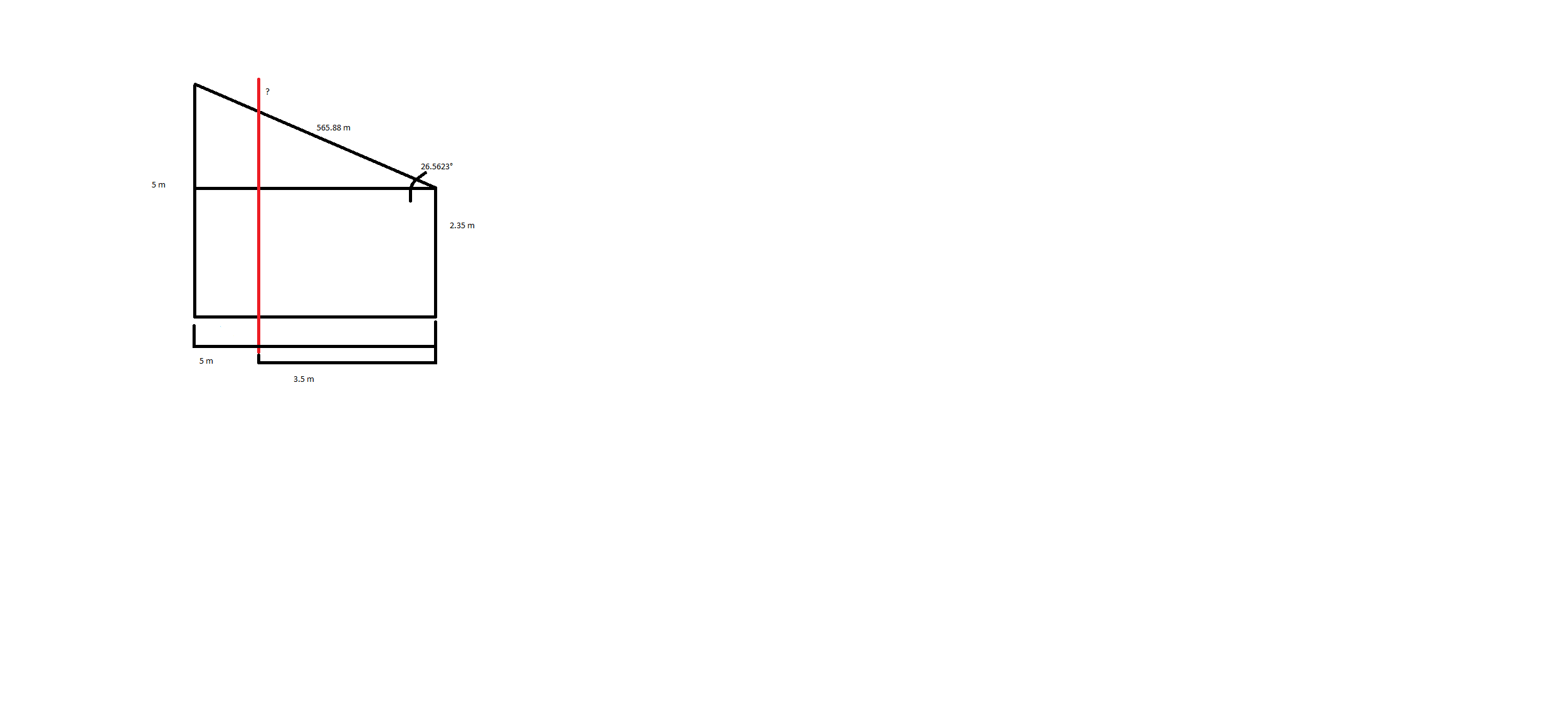
Dans le dessin que vous pouvez voir en dessous, le trait rouge est le plan de coupe, et ce que je voudrai savoir, c'est à quelle hauteur il coupe le haut du toit (là où il y a le ?). J'ai pris un triangle rectangle pour pouvoir mesurer l'angle indiqué sur le dessin, et si je trouve la hauteur de l'opposé à cet angle (opposé qui se situe sur le triangle plus petit), ça me permettra (en l'additionnant aux 2.35 m de trouver la hauteur qui m'intéresse.
J'ai calculé l'hypoténuse (racine de (265 au carré + 500 au carré) = 565.88 m.0
Ensuite, si j'utilise le sinus, qui est égal à l'opposé sur l'hypoténuse, cela me fait un angle de :
  sin = 265/565.88 = 0.4635 (radians je suppose)
Je le met en degré, pour cela, vu que sur pi/2 radians, il y en a 0.46, alors sur 90°, il y en a....
(0.4635*90)/pi/2 = 26.5623 °
Ensuite, pour trouver la taille de l'opposé du triangle rectangle plus petit, opposé qui est donc le trait rouge du petit triangle, j'ai décidé d'utiliser une tangente. La tangente = opp/adj, donc opp = tan * adj .
Alors opp = 350.5 * tan(26.5623)
              = 2465 et quelques
MAIS C'EST IMPOSSIBLE !!!! C'est là ou je n'y arrive pas, je pense que mon raisonnement est bon, mais je ne vois pas pourquoi les résultats sont impossibles, je me casse la tête dessus depuis tois jours au moins.
Alors si une âme charitable pouvait m'aider, je lui serai grandement reconnaissant, car c'est pour lundi.
Merci d'avance, par pitié, aidez moi !!!!