Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 23-01-2015 23:03:29
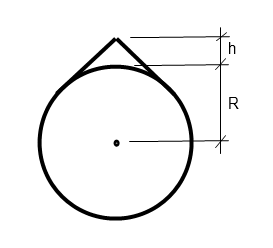
Câble entorant la Terre
#0 Pub#2 - 23-01-2015 23:13:50#3 - 24-01-2015 07:30:31
Câble entourantt la TerreBonjour, Code:2*R*( tan(a) - a ) = 1 h = R*( 1/cos(a) - 1 ) En utilisant les développements limités de tan et cos, on obtient Code:h = (9*R/32)**(1/3) = 121,64 m #4 - 24-01-2015 10:24:08
Câble entourant la TerrPar dichotomie sur l'angle x ou se fait la tangence avec Y la demi longueur de corde tendue : #5 - 24-01-2015 11:03:38#6 - 24-01-2015 11:14:03
Câbe entourant la Terresalut. #7 - 24-01-2015 11:29:49
Câble entouran la TerreLa réponse est h = 121.644733533488... arrondi à 122 mètres. #8 - 24-01-2015 13:00:16
Câble entourant la TrrePar jeu d'angle et de tangente, on arrive aux relations suivantes: #9 - 24-01-2015 16:15:39
câbke entourant la terreQue de bonnes réponses ! Ce résultat étonnant valait bien un peu de géométrie ! #10 - 24-01-2015 19:03:20
Câble entourant la eTrrePour x petit, atan(x)=x-x^3/3-... #11 - 27-01-2015 07:46:29
Câble entoourant la TerreMerci à tous pour votre participation. #12 - 27-01-2015 08:05:33#13 - 01-02-2015 23:42:41
câble entoueant la terreBonjour, Je ne vien sur se site que pour faire croir que je suis treise intélligens. #14 - 02-02-2015 00:19:27
Câbe entourant la TerreComme l'angle est "très petit", on a pu faire des approximations sur les fonctions trigo (je crois que ça s'appelle des développements limités). #15 - 02-02-2015 07:23:11
Câble entourant la Terrre
On n'a pas une expression générale, car il faut résoudre une équetion qui fait intervenir a et tg(a) (a est le demi-angle des droites joignant le centre de la terre aux 2 points de tangence).
Le calcul montre que, dans ce cas, h=0,573 m
Oui, h varie de 0,50 m (pour R=0) à l'infini (pour R->∞). Réponse rapideSujets similaires
Mots clés des moteurs de recherche |
 | ||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | ||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.