 |
#1 - 30-03-2015 18:37:07
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3801
Un zig zag uqi n'est pas un z
Bonjour à tous,
Une petite énigme géométrique pas bien compliquée.
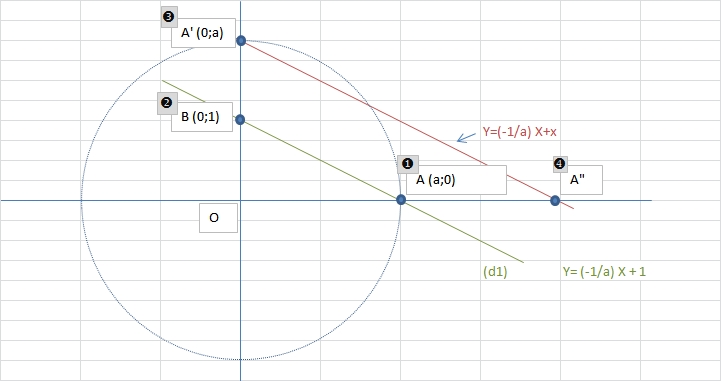
Dans le repère orthonormé Oxy, on place un pt A sur Ox.
1) Tracer le segment d1 qui passe par les pts A et (0,1)
2) Porter le pt A' sur Oy tel que OA'=OA
3) Porter le pt A'' sur Ox tel que A'A'' parallèle à d1.
Que représente OA'' par rapport à OA ?
Si on avait mis A'' en premier, est il possible de retrouver A ?
Bon amusement.
#2 - 30-03-2015 19:32:32
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
Un zig zag qui 'nest pas un z
D'après Thalès OA/1=OA"/OA' or OA=OA' donc OA"=OA^2
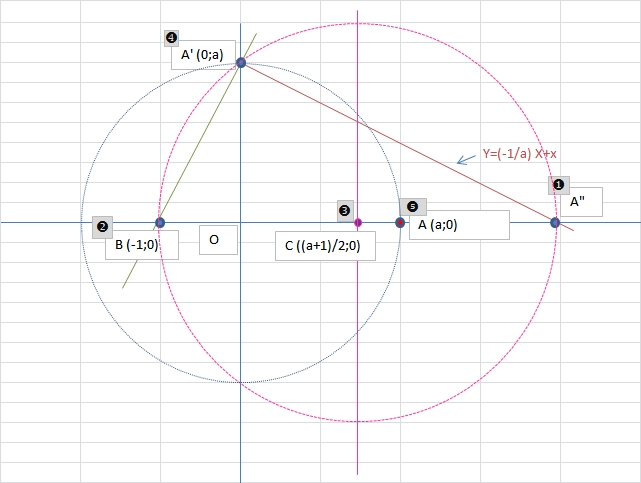
Si on avait donné A" en premier, il aurait suffi de tracer un cercle de diamètre BA" où B(-1,0). Ce cercle couperait oy en A'. On place A sur ox tel que OA=OA'.
Voilà
#3 - 30-03-2015 20:07:35
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3801
in zig zag qui n'est pas un z
Parfait kossi-tg, et ça n'a pas traîné !
#4 - 31-03-2015 00:36:26
- pycool
- Amateur de Prise2Tete
- Enigmes résolues : 32
- Messages : 3
un zig zag qui n'est oas un z
Bonjour,
Je pense que l'on fait appel à Thalès:
On a un triangle OA'A"
(d1) parallèle à (A'A") et OA' non nul
donc OA/OA" = Oj/OA' = jA/A'A"
OR Oj=1 ET OA=OA'
Donc OA"=OA²
Si on place A" en premier, on trace A' quelconque tel que OA' >1
puis on trace d1 passant par (0;1) coupant Ox en A
Pour Thalès la réciproque est vrai.
donc:
OA= racine²(OA")
#5 - 31-03-2015 08:35:17
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
Un zig zag qui n'estt pas un z
Bonjour,
D'après le théorème de Thalès
1 / OA' = OA / OA"
d'où OA" = OA ^ 2
Soit I le point de coordonnées (1,0). On trace le cercle de diamètre OI, et la perpendiculaire à Ox passant par A", qui coupe le cercle en J (et J'). Dans le triangle rectangle OIJ, on a la relation
OJ ^ 2 = OI * OA"
La distance cherchée OA est égale à OJ
#6 - 31-03-2015 09:01:36
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3801
un zig zag qui n'est pas yn z
Pycool, il faudrait revoir la construction à partir de A'', ça ne marche pas à mon avis.
Enigmatus, c'est bon, mais si 0A''>1 ?
#7 - 31-03-2015 09:14:37
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
un zig zag qui n'est pas yn z
nodgim a écrit:c'est bon, mais si 0A''>1 ?
Il y a une autre construction qui marche dans les deux cas. Soit K le point de coordonnées (-1,0). Le cercle de diamètre KA" coupe l'axe Oy en P (et P'). La distance OP est égale à OA.
#8 - 31-03-2015 10:29:05
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3801
Un zig zag qui n'est as un z
Oui, c'est ça bravo Enigmatus !
#9 - 31-03-2015 18:57:05
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1819
U zig zag qui n'est pas un z
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#10 - 31-03-2015 20:01:41
- morgu_07
- Amateur de Prise2Tete
- Enigmes résolues : 41
- Messages : 9
Un zig zzag qui n'est pas un z
OA'' représente le carré de OA!
Maintenant qu'on sait ça, placé OA par rapport à OA'' il nous suffit de prendre la racine carrée de OA''!  (mais ça m'étonnerait que ce soit la réponse attendu à cette 2ème question)
#11 - 01-04-2015 09:25:04
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3801
Un zig zag qi n'est pas un z
NickoGecko c'est parfait, et très beau dessin en prime.
Morgu, c'est bien ça pour la 1ère question, bien qu'on ne trouve pas la démonstration. La seconde question nécessite une construction distincte.
#12 - 01-04-2015 17:28:47
- Fito11235
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 173
Un zig zag qui n'eest pas un z
Coucou,
OA'' est l'image de OA par l'homothétie de centre O et de rapport OA.
Par thalès OA''/OA = OA'/1 OA''/OA = OA/1 soit OA'' = OA^2
Pour retrouver A, on cherche à construire un segment de longueur racine de OA''
J'appelle B le point de coordonnées (-1;0).
Le cercle de diamètre BA'' coupe Oy au point A'.
Il ne reste qu'à reporter OA' sur Ox.
Merci  .
#13 - 01-04-2015 18:18:44
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3801
un zig zag qui n'est pad un z
Fito, c'est tout bon également, bravo.
#14 - 02-04-2015 08:43:40
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3218
- Lieu: Luxembourg
Un zig zag uqi n'est pas un z
On a: OA''=OA², mais pour la construction inverse je sèche encore. Affaire à suivre ...
#15 - 02-04-2015 09:07:59
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3801
un zig eag qui n'est pas un z
Francky, oui c'est bon pour la 1ère question.
#16 - 02-04-2015 21:48:17
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3218
- Lieu: Luxembourg
Un zig zzag qui n'est pas un z
Bien vu: le triangle BA’A’’ est rectangle en A’
Donc: OA’²=BO.OA’’ => OA’²=x² => OA’=x
#17 - 03-04-2015 09:05:09
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3801
un aig zag qui n'est pas un z
Bravo à tous, pas grand chose à ajouter. Par la voie algébrique, on ne sait pas calculer directement la racine carrée d'un nombre. Il faut utiliser un algorithme. Par la voie géométrique, c'est direct, mais moins précis. De la figure géométrique qui donne la racine carrée d'un réel positif x, on en déduit:
racx=sin(arc cos((x-1)/(x+1)))*(x+1)/2.
|
 |
Accueil
