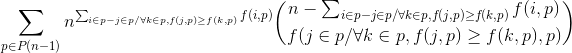|
#1 - 12-04-2015 12:44:46
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
les chevalières fe la table ronde (prologue)
Voici la première d'une série d'énigmes tournant autour du même sujet. Certaines seront corsées, car faisant appel à des techniques mathématiques inhabituelles. Mais nous allons commencer par du classique.
n nobliaux sont assis autour d'une table ronde (ce qui sera important plus tard), et se répartissent n-1 chevalières (ce qui est important pour le mauvais jeu de mots du titre). Un nobliau peut avoir plusieurs ou même la totalité des chevalières.
Combien existe-t-il de répartitions différentes de ces n-1 chevalières ?
Pour la bonne compréhension de l'énoncé, deux répartitions peuvent être symétriques et néanmoins différentes : elles ne sont identiques que si chaque nobliau a le même nombre de chevalières dans les deux répartitions.
PS1 : une chevalière est une bague, à ne pas confondre avec la chevaleresse, qui est l'équivalent féminin du chevalier.
PS2 : les chevalières ne sont pas distinctes ; mais les nobliaux, oui. Par exemple, s'il y a 8 nobliaux (et donc 7 chevalières), une répartition possible est [25000000]. Par ailleurs, les répartitions [00000052] ou [02500000] sont deux autres répartitions, différentes de la première.
#2 - 12-04-2015 12:52:51
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Les chevalières de la tabble ronde (prologue)
Une dame A à droite d'une dame B est il équivalent à: B à droite de A ?
Autrement dit, chaque dame est elle distincte des autres (dans le problème bien sûr) ? Même question pour les chevaliers.
#3 - 12-04-2015 14:32:08
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Les chevalières de la tabble ronde (prologue)
@nodgim : j'ai rajouté des précisions à la fin de l'énoncé pour éviter toute ambiguïté.
#4 - 12-04-2015 17:19:27
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
les chevalières de la yable ronde (prologue)
Je veux bien comprendre que la répartition [00000052] est différente de [25000000], puisqu'elle "tourne dans l'autre sens". Mais je ne comprends pas pourquoi la répartition [02500000] est différente de [25000000]: la table étant ronde, on peut commencer à compter d'où on veut, non ?
#5 - 12-04-2015 18:37:17
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Les cheavlières de la table ronde (prologue)
Compris Ebichu. Je me disais que le terme de chevalière pour la dame du chevalier, c'était un peu...cavalier. J'en ris encore.
#6 - 12-04-2015 18:51:54
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Les chevalières de la taable ronde (prologue)
Pour moi, ce sera C(2n-2,n-1).
Quand on distribue m objets dans n cases, si on peut mettre tous les objets dans une seule case, le nombre de combis est C(n+m-1, m).
#7 - 12-04-2015 19:13:28
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Les chevalières de lla table ronde (prologue)
@Franky1103 : [02500000] est différente de [25000000] car si tu es à la place du 1er nobliau, tu préfères la 2e répartition qui te donne 2 bagues, à la 1e qui ne t'en donne aucune. Oublie que la table est ronde pour le moment, ça ne servira qu'à partir de l'énigme suivante.
@nodgim : je vois 2 erreurs dans ta formule. Elle donne des nombres non entiers, c'est plutôt inquiétant  Une petite démo, au moins les grandes lignes ? Une petite démo, au moins les grandes lignes ?
#8 - 12-04-2015 19:35:19
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Les chevlières de la table ronde (prologue)
J'ai corrigé et mis un commentaire.
#9 - 12-04-2015 19:39:55
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Les chevalières de la table ronde (proloue)
@nodgim : parfait, c'est résolu !
#10 - 14-04-2015 18:08:35
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1823
Les chevlières de la table ronde (prologue)
Bonjour
Je me suis d'abord lancé sur les partitions d'entiers, puis sur le nombre de combinaisons de chacune des décompositions en sommes pour les premiers cas de 2, 3 .... à 6 nobliaux ...
exemple pour 3 nobliaux / 2 chevalières, il y a 2 décompositions possibles:
(a) 2 = 2 + 0 + 0
(b) 2 = 1 + 1 + 0
sachant que l'ordre importe, il faut donc chercher le nombre d'"anagrammes" possible de chacune des lignes ci-dessus :
pour (a) il y a 3 permutations (3 positions du "2")
pour (b) il y a aussi 3 possibilités
soit 6 possibilités au total
exemple pour 6 nobliaux / 5 chevalières, il y a 7 décompositions possibles:
(a) 5 = 5 + 0 + 0 + 0 + 0 + 0
(b) 5 = 4 + 1 + 0 + 0 + 0 + 0
(c) 5 = 3 + 2 + 0 + 0 + 0 + 0
(d) 5 = 2 + 2 + 1 + 0 + 0 + 0
(e) 5 = 2 + 1 + 1 + 1 + 0 + 0
(f) 5 = 3 + 1 + 1 + 0 + 0 + 0
(g) 5 = 1 + 1 + 1 + 1 + 1 + 0
idem le nombre d'"anagrammes" possible de chacune des lignes ci-dessus est :
pour (a) : cinq fois le "0", donc 6!/5! = 6 possibilités
pour (b) : quatre fois "0" donc 6!/4!= 30 possibilités
pour (c) : idem
pour (d) : trois fois "0" et deux fois "2" soit 6!/(2!3!) = 60
pour (e) : trois fois "1" et deux fois "1" soit 6!/(2!3!) = 60
pour (f) : 6!/(2!3!) = 60
pour (g) : 6
soit 252 possibilités ...
En fait j'ai trouvé la généralisation du problème autrement, du côté des "compositions" et en anglais le mot-clé "multiset"
http://en.wikipedia.org/wiki/Multiset#C … _multisets
capture d'écran zoomable :
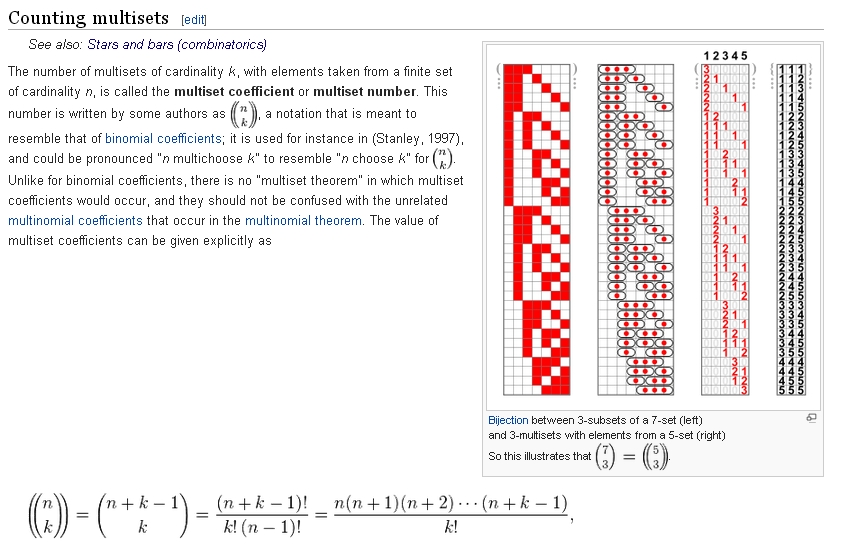
C'est la troisième représentation graphique de la distribution de "3 parmi 5" qui illustre le mieux à mon sens le problème posé (à adapter toutefois)
du coup la formule donnant le nombre total de manières de répartir k éléments dans un ensemble de cardinal n est : (n+k-1)! / k!(n-1)!
Ici on a n nobliaux et k=n-1 chevalières
La formule devient : (2n-2)! / (n-1)!(n-1)!
On retrouve,
pour 2 chevalières et n=3 nobliaux , (4!) / (2! 2!) = 6
pour 5 chevalières et n=6 nobliaux , (10!) / (5! 5!) = 252
merci et intéressant, je vais pouvoir me replonger dans le problème "du pain aux raisins" sur rightanswer ....! 
(edit : ... que je n'avais pas résolu ... il s'agit de 100 raisins dans 1kg de pâte formant 10 pains - question : et si un pain ne contenant aucun raisin ? )
A+
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#11 - 14-04-2015 21:03:58
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Les chevalières de la table ronde p(rologue)
#12 - 14-04-2015 22:21:01
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Les chevalières ed la table ronde (prologue)
@NickoGecko : bravo, c'est bien ça, avec les explications détaillées en prime !
@titoufred : en effet, félicitations ! Quel raisonnement as-tu suivi ?
#13 - 15-04-2015 02:02:32
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
Les chevalières de a table ronde (prologue)
Soit n le nombre de chevaliers et donc n-1 le nombre de bagues.
Soit P(n-1) l'ensemble des partitions de n-1.
Alors le nombre de répartitions vaut :
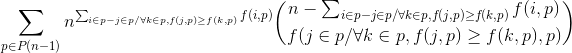
Avec f la fonction qui donne le nombre d’occurrences de i dans p.
J'ai pas trouvé plus simple 
Exemple pour n = 6 :
1+1+1+1+1 donne (6 5) répartitions.
2+1+1+1 donne 6*(5 3) répartitions.
3+1+1 donne 6*(5 2) répartitions.
4+1 donne 6*(5 1) répartitions.
3+2 donne 6*(5 1) répartitions.
2+1+2 donne 6*(5 2) répartitions.
5 donne (6 1) répartitions.
Soit au total 252 répartitions.
#14 - 15-04-2015 02:17:43
- dbab3000
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 111
les chevalières de la table ronde (prolohue)
J'espère que je ne suis pas en retard,on a:
La fonction Fₓ(n) qui représente le nombre de répartition tel que x est le nombre de nobliaux et n le nombre de chevalières,on va utiliser n généralement et on va varier x :
Pour 1 nobliau on a n chevalières on a une seule répartition alors F₁(n)=1.
Pour 2 nobliaux on a n chevalières, on va s'intéresser au premier nobliau s'il prend k chevalières il va laisser n-k chevalières à l'autre alors il y a n+1 répartitions qui peut s'écrire sous cette forme
F₂(n)=somme (de k=0 à n) F₁(k)=n+1,cette relation n'est pas évidente au début mais après ça devient plus clair pourquoi on l'utilise .
Pour 3 nobliaux on a n chevalières, on va encore s'intéresser au premier nobliau s'il prend k chevalières il va laisser n-k au deux autres ce qui donne F₂(n-k) répartition mais puisque k varie de 0 à n le nombre de répartition est
F₃(n)=somme (de k=0 à n) F₂(k)=(n+1)(n+2)÷2
Alors généralement le nombre de répartition est
Fₓ(n)=somme (de k=0 à n) Fₓ₋₁(k)
Mais dans notre cas la réponse est:
Fn(n-1)=somme (de k=0 à n-1) Fn₋₁(k)
J'espère que je n'ai pas commis d'erreur de raisonnement ou de calcul.
PS:La rédaction était plus pénible que la réflexion ^^.
Bonne nuit.
#15 - 15-04-2015 10:25:27
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Les chevalières de la table roonde (prologue)
@dbab3000 : ton raisonnement et ta formule sont corrects, bravo. Par contre, il est possible d'exprimer le résultat de manière nettement plus simple, et donc plus rapide à calculer. Spoiler : [Afficher le message] En exprimant F4(n) avec une formule du même type que F3(n)=(n+1)(n+2)÷2, tu devrais entrevoir le résultat final.
@Sydre : Le résultat de ton exemple (80) est faux, alors que les explications juste avant sont correctes. Erreur de calcul ?
Quant à ta formule, je pense qu'elle est fausse également, même si elle peut fonctionner sur les petits cas. Spoiler : [Afficher le message] Il n'y a pas de raison de distinguer les "j" des autres nombres, il ne devrait pas y avoir de puissance de n dans ta formule.
#16 - 15-04-2015 11:47:29
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
Les chevalièrs de la table ronde (prologue)
Effectivement, je voulais dire 252 
#17 - 15-04-2015 12:04:17
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Les chevalières de la table ronde p(rologue)
@Sydre : 252 c'est bon  Il te reste à résoudre le cas général. Il te reste à résoudre le cas général.
#18 - 15-04-2015 15:07:30
- dbab3000
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 111
les chevalières de la table ronde (prokogue)
Salut j'avais le pressentiment que ce n'était pas encore fini mais j'étais trop fatigué pour continuer le calcul, après un changement de batterie ^^, je vais rectifier mon explication :
F₁(n)=1
F₂(n)=n+1
F₃(n)=(n+1)(n+2)÷2
F₄(n)=(n+1)(n+2)÷2(n+3)÷3
F₅(n)=(n+1)(n+2)÷2(n+3)÷3(n+4)÷4
Alors la formule générale est:
Fₓ(n)=produit(de k=1 à x-1) (n+k)÷k tel que x≥2 et F₁(n)=1
Dans notre cas la formule est :
Fn(n-1)=produit(de k=1 à n-1) (n-1+k)÷k =(2n-2)! ÷(n-1)!(n-1)!
Bonne journée.
#19 - 15-04-2015 18:02:13
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Les chevalières de la tale ronde (prologue)
Félicitations à tous ceux qui ont trouvé. Avec l'explication de NickoGecko, tout est dit. Pour les anglophobes, cette page fournit une explication sensiblement équivalente : http://fr.wikipedia.org/wiki/Combinaiso … .A9titions
Demain, avec l'étape suivante du problème, nous aborderons des thèmes un peu moins... disons, standard.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum