Je suppose que pour ce genre de championnat, il est préférable de connaitre quelques formules telles que celles du Heron donnant l'aire du triangle (A) et des relations avec le rayon du cercle inscrit (r) et circonscrit (R).
[TeX] \fbox{A=\sqrt{s(s-a)(s-b)(s-c)}
A=rs
abc=4srR}[/TeX]
avec s le demi-périmètre

ce qui donne [latex]2R=\frac{7\times 25 \time sqrt2 \times sqrt3} 6[/latex]

On peut ensuite avoir en tête quelques astuces de 'physicien' :
[TeX]\frac{\sqrt2} 2 = 0.707 \approx 0.7 + 1%[/TeX]
[TeX]\frac{\sqrt3} 3 = 0.577 \approx 0.6 - 4% [/TeX]
[TeX]\frac{\sqrt5} 5 = 0.447 \approx 9/2 -1% [/TeX]
[TeX]\frac{\sqrt6} 6 = 0.408 \approx 0.4 + 2%[/TeX]
ce qui donne
[TeX]0.4 \times 25 = 10
10 \times 7 = 70
70 + 2 % = 71.4[/TeX]
Le diamètre minimal de la table est donc 72 cm pour que les Pinocchios vivent sans heurt autour de leur table.

Arrondir à 71cm est idiot ici mais c'est la réponse attendue c'est vraiment un truc de mathématiciens

Il y a t'il plus simple ?

Il suffit de construire un triangle dont les côtés font 70cm, 60cm, et 50cm. La table sera le cercle circonscrit a ce triangle, et les 3 Pinocch aux sommets.
Pour calculer le rayon du cercle circonscrit, on utilise la formule :
[TeX]S=\frac{abc}{4R}[/TeX]
L'aire du triangle peut être calculée par la formule de Héron
[TeX]S=\sqrt{p(p-a)(p-b)(p-c)}[/TeX]
où [latex]p=\frac{a+b+c}2[/latex]

Application numérique :
[TeX]p=90cm
S=6\sqrt{6}cm^2
R=\frac{35}{4\sqrt6}cm
d=\frac{35}{2\sqrt6}\approx71,44cm[/TeX]
Faudrait pas qu'un des 3 se mette à mentir plus que la normale, sinon ça fout tout en l'air

Appelons les P(ère), M(ère) et F(ille) et mesurons en décimètres.

Leurs positions autour d'une table définissent un triangle inscrit (P,M,F) à un cercle (la table).

On doit avoir d(P,M)>= 4+3, d(P,F)>=4+2 et d(M,F)>=3+2.

On a un triangle T de côtés a,b,c = 5,6,7 et de demi-périmètre p=9

La formule de Héron nous donne la surface S = racine(p.(p-a).(p-b).(p-c)) = racine(9.4.3.2)=6.racine(6).

La loi des sinus nous donne le rayon du cercle : R=abc/(4S)=5.6.7/(4.6.racine(6)) et yapuka, soit environ 71,44 cm.

Merci à Google pour les deux formules ci-dessus.

Cette table est de la taille du cercle circonscrit à  un triangle de côtés 50 60 et 70cm

r= 50*60*70 / 2S
r=   50 * 60 * 70 / rac( (90*(90-50) * (90-60) * (90-70) )

r= 50*60*70 / rac (90*40*30*20)
r= ....

Je reviens...

r= 182,88 cm ? <Euh...  / 2 = 91 cm>



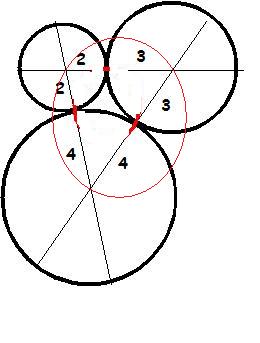
Pfff, en regardant le dessin, je penche plutot pour 73 ou 74, or la case réponse valide 71. Erreur dans les calculs?

J'ai une solution un peu calculatoire alors sans instruments c'est un peu long

Les positions des trois personnages définissent un triangle ABC de côtés a=50 cm , b=60 cm et c=70 cm . On calcule l'aire du triangle avec la formule de Heron A=600.rac(6) . Le diamètre de la table est celui du cercle circonscrit au triangle ABC : D=abc/2A = 175/rac(6) .

Vasimolo

Pinocchio, Pinocchia et Pinocchi se trouvent chacun aux sommets d'un triangle dont les côtés mesurent :
a  =  40 + 30  =  70 cm
b  =  40 + 20  =  60 cm
c  =  30 + 20  =  50 cm


La formule de Héron nous donne l'aire de ce triangle :
A = √(s.(s-a).(s-b).(s-c))
avec s = (a+b+c)/2

Soit s = 90
et :
A  =  √(90x20x30x40)
A  =  √(2x3x3x5 x 2x2x5 x 2x3x5 x 2x2x2x5)
A  =  2x2x2x3x5x5.√(2x3)
A  =  600.√2.√3


La table est le cercle circonscrit à ce triangle, et son diamètre est :
D  =  (a.b.c)/(2A)

D  =  70x60x50 / (1200.√2.√3)
D  =  175 / (√2.√3)
D  =  175 / (1,414 x 1,732)
D  =  71,46

Le diamètre de la table est donc de 71 cms


A noter que sans les arrondis de √2 et √3, le diamètre exact est de 71,44 cms


Merci à toi rivas pour ce problème très sympa, et merci à Wiki pour les deux formules utilisées

Pour info TiLapiot est en train de refaire rétroactivement toutes les énigmes du site:

Oui Franky, mais ce n'est pas ma faute : j'aime la beauté de certaines de vos énigmes, qu'elles soient récentes ou anciennes...
alors j'ESSAIE... souvent vainement de les résoudre

Et un jour, qui sait si, avec ou Gepetto, je posterai ma propre énigme

Le dernier post de TiLapiot ici mériterait un "J'aime" si on était sur Facebook. On prend vite ce genre d'habitudes de m***e

Effectivement, il y a une raison pour laquelle les vieilles énigmes restent sur le forum : de temps a autre, quelqu'un voudra curioser et en refaire quelques-unes, et je ne peux que lui donner raison.