Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 05-02-2019 11:10:30
un hrxagoneBonjour à tous,
#0 Pub#2 - 05-02-2019 15:22:24
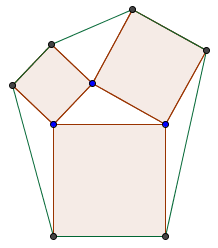
Un hexagonneLes quatre triangles ont la même aire. #3 - 05-02-2019 19:08:57#4 - 05-02-2019 19:30:36
Un hexagonneBonjour, #5 - 05-02-2019 21:59:14
Un hexagoneeBonjour #6 - 05-02-2019 22:10:27#7 - 06-02-2019 10:52:01
Un hexagoeJe trouve 40.62 #8 - 06-02-2019 19:28:56#9 - 06-02-2019 23:17:09
nU hexagoneBonjour, #10 - 07-02-2019 19:14:24#11 - 10-02-2019 16:23:02
Un hexagonneFélicitations aux participants qui ont tous bien analysé le problème. Si tout le monde a eu recours à la formule de Héron pour l'aire d'un triangle, l'égalité des aires des 4 triangles a été démontrée soit par le sinus, soit par un argument purement géométrique. Réponse rapideSujets similaires
|
 | ||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | ||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.