Enigme Particularité de 2017 @ Prise2Tete

Franky1103 · #1

En mathématiques, deux nombres premiers jumeaux sont deux nombres premiers dont la différence est de 2, comme par exemple 3 et 5 ou 2027 et 2029. Comment appelle t’on un couple de nombres premiers dont la différence est de 6, comme par exemple 5 et 11 ou 2011 et 2017 ?

fvallee27 · #2

hello Franky, tu commences l'année en pleine forme, sexy-man !

nodgim · #3

Des nombres sexy je crois. A ne pas confondre avec le 69 de Gainsbourg...

Ebichu · #4

Très malin

godisdead · #5

après une petite recherche : sexy

Sydre · #6

C'est sexy cette histoire

franck9525 · #7

p=q+4 => cousin prime number
p=q+6 => sexy prime number

aunryz · #8

Ma mère m'a interdit d'écrire la réponse en clair

c'est si sec !

nobodydy · #9

L00ping007 · #10

Sexy !
Et des nombres premiers dont la différence vaut 4 sont des nombres premiers cousins

Klimrod · #11

Bonjour Franky,

Tu vas peut-être réussir l'exploit de l'énigme mathématique ayant reçu le plus de réponses exactes !

Pour me démarquer de mes petits camarades qui auront certainement illustré leur nombre sexy avec des 69 plus ou moins censurables par Ash, voici un peu de littérature sérieuse :

Nombre premiers jumeaux
Un couple de nombre premiers est dit "jumeaux" s'ils sont séparés de 2.
Le plus grand couple de jumeaux connu est actuellement 2003663613 × 2^195000 ±1.
Conjoncture : y a t'il un nombre infini de nombres premiers jumeaux ?
Remarque : Il ne peut pas exister de triplets de jumeaux, car l'un des nombres p, p+2, p+4 est divisible par 3.

Nombre premiers cousins
Un couple de nombres premiers cousins est un couple de premiers de la forme (p, p+4).
Les premiers cousins sont (3, 7), (7, 11), (13, 17), (19, 23), (37, 41)...
Comme pour les jumeaux, il ne peut pas exister de triplets de cousins, car l'un des nombres p, p+4, p+8 est divisible par 3.

Nombre premiers sexy
Un couple de nombres premiers sexy est de la forme (p, p+6), et tient son nom du latin "sex" qui signifie 6 (mais pourquoi donc cette nécessité de préciser l’étymologie ? )
Les premiers sexy sont (5,11), (7,13), (11,17), (13,19), (17,23), (23,29), (31,37), (37,43)...

Ce qu'il y a d'intéressant avec les nombres premiers sexy, c'est que non seulement ils forment des couples, mais également des triplets ou des quadruplets ou même des quintuplets. Par exemple, (5,11,17,23,29) est un quintuplet sexy !

Le théorème de Green-Tao
Tout ça pour en arriver au théorème de Green-Tao, qui date de 2004, et qui a valu à Tao la médaille Field (le prix Nobel des maths) en 2006.

(5,11,17,23,29) est une suite arithmétique (de raison 6), de longueur 5, composée seulement de nombres premiers.
Mais peut-on trouver une telle suite, disons, de longueur 6 ?... Oui !
On a par exemple (7,37,67,97,127,157), de raison 30 et de longueur 6 !
Et si on se fixe pour longueur 25 ?
Bien sûr, on met un peut plus de temps dans la recherche, mais avec du courage, on trouve la suite (6171054912832631 + 81737658082080 × n | 0≤n≤24) (Plus longue suite arithmétique de nombres premiers connue, trouvée en 2008).

Ce que Green et Tao ont démontré, c'est que pour n'importe quelle longueur fixée, il est possible de trouver une suite arithmétique de nombres premiers de cette longueur. Malheureusement dans cette histoire, ils ne disent pas comment la trouver !

Et la conjoncture de Polignac ?
La conjecture de Polignac, qui généralise la conjecture des premiers jumeaux, prétend que pour n'importe quel k pair, il existe une infinités de couples de nombres premiers de la forme (p, p+k). On en attend toujours une démonstration...

Voilà, voilà... Y'a encore du boulot pour les courageux !
Klim.

Franky1103 · #12

@Klimrod
Il y a en effet beaucoup de bonnes réponses.
Merci pour toutes les précisions que tu as apportées et que je ne connaissais pas pour la plupart: les participants les verront lorsque le temps sera écoulé.
Sans être réellement dans le sujet, j'ai aussi récemment lu un article sur la découverte d’une régularité cachée dans la suite des nombres premiers que voici:
http://www.pourlascience.fr/ewb_pages/a … -36713.php
A+

Lui-meme · #13

SEXY

Pour ces nombres premiers, le terme « sexy » est un jeu de mot basé sur le mot latin pour « six » : "sex".

Il est bien connu qu'un 6 peut en retourner un autre...

nodgim · #14

@ Francky: au sujet de la soi-disante " régularité " des nombres premiers récemment découverte, découverte qui a aussi eu l'honneur d'un article dans "Sciences et Vie", je me permets d'y apporter mes remarques.

Il s'agit avant tout d'une sorte d'anomalie de répartition: il n'y a pas équirépartition, comme on aurait pu s'y attendre, entre les 4 groupes de nombres premiers: ceux qui se terminent par 1, 3, 7 et 9. Je n'ai plus les chiffres en tête, mais la différence de répartition, au lieu d'être 25 % pour chaque groupe, est déséquilibrée, mais pas de manière spectaculaire. Si quelqu'un a encore l'article en main, ou s'il se souvient des chiffres....Ce déséquilibre se résorbe quand on regarde cette répartition avec beaucoup beaucoup de nombres premiers, ce qui signifie finalement qu'il s'agit d'une anomalie ponctuelle. Je peux me tromper, mais je ne pense pas que les mathématiciens pourront tirer le moindre enseignement de cette anomalie, en dépit de ce que certains d'entre eux ont dit dans ces articles. Bref, la lecture de cet article m'a fait vraiment rire : Car si on donnait la même importance à toutes les conjectures non résolues, on n'aurait pas assez d'une revue spécialisée pour ne parler que de ça ! Bref, j'ai personnellement trouvé cette soit disante " découverte " comme un non événement, et je parie aujourd'hui qu'on n'est pas près d'en reparler avant longtemps.
Il faut vraiment se méfier des annonces tapageuses, qui sont devenues la spécialité des revues de vulgarisation scientifique. Il en est du journalisme scientifique comme du journalisme tout court: il faut vendre, quitte à oublier la déontologie de la science, qui ne devrait être que prudence et humilité.

Cette petite réflexion en appelle une dernière: je trouve un peu curieux que des matheux passent du temps à observer les nombres premiers comme les astronomes observent le ciel. Je ne voyais pas le travail du mathématicien comme ça. Mais bon, pourquoi pas après tout ? Ne parle t'on pas aujourd'hui de mathématique heuristique ? Ce qui est tout de même un fameux contre sens !

NickoGecko · #15

Bonne Année !

aunryz · #16

Bon début de soirée

Concernant l'article évoqué qui dit
"Comment expliquer qu’il est plus rare de trouver deux nombres premiers consécutifs avec le même chiffre final ?"

Il me semble qu'il y a une explication simple (?)
qui n'est pas évoquée

soit un nombre premier se terminant par un 9
Le nombre* suivant se terminant également par un 9 a
1 chance sur 2 d'être multiple de 3
1 chance sur 6 d'être multiple de 7
1 chance sur 10 d'être multiple de 11
...
1 chance sur n-1 d'être multiple de n

Alors que le nombre se terminant par un 1, un 3 ou un 7 qui le suit a

1 chance sur 3 d'être multiple de 3
1 chance sur 7 d'être multiple de 7
1 chance sur 11 d'être multiple de 11
...
1 chance sur n d'être multiple de n

Ce qui justifie en partie au moins
(je laisse aux compétents le soin de chiffrer cet écart)
la plus grande rareté de l'un
par rapport à l'autre
parmi les nombres premiers

(n'est-il pas ?)

Bonne fin de soirée

_________
* par erreur j'avais mis "nombre premier" !
c t'où m'ouah ! ça

scrablor · #17

Une image suffit-elle pour répondre à la question ?

Franky1103 · #18

Merci à toutes et à tous pour votre participation, vos illustrations et également vos remarques que je vous laisse découvrir (concernant surtout l'article de presse cité).
La réponse "sexy" est en effet un jeu de mot basé sur le mot latin "sex" (soit six).
Les mathématiciens ne manquent pas d'humour; les physiciens non plus d'ailleurs, quand on voit le nom donné à certaines particules subatomiques ou à leurs propriétés.

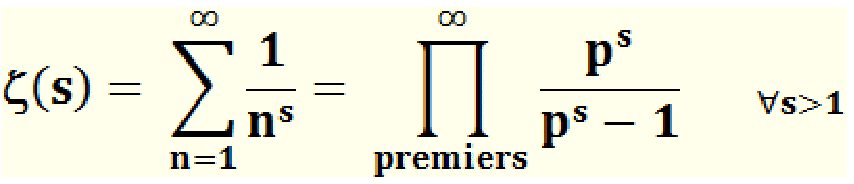
Personnellement, ce qui m’épate le plus, c’est que l’identité d'Euler ci-dessus, basée sur la fonction Zêta de Riemann jette un pont entre les nombres premiers et les nombres entiers ordinaires. On peut alors se demander si une loi de répartition des nombres premiers existe peut-être.

ash00 · #19

Va falloir que je modère ce message en particulier !

aunryz · #20

[à ceux qui ne dorment pas encore]

...

[à ceux qui s'éveillent]

...

Je profite de ce fil de réflexion
pour demander si l'on connait un (des) nombre(s) du type
1234567891011...N (écrit avec les chiffres de la suite des nombres entiers jusque N)
qui soit premier

par exemple
123456789101112131415161718192021222324252627282930313233343536373839 l'est-il ? (sauf erreur de ma part, ceux qui le précèdent ne le sont pas)

à priori la réponse serait ... bien sur
il n'y a pas de raison (les nombres premiers ne l'étant pas trop) que les nombres premiers "évitent" une suite de nombre contenant potentiellement (apparemment) des leurs

... merci d'avance aux esprits éveillés et nourris .

Bonne Inuits

Klimrod · #21

Il existe un autre angle d'attaque pour tenter de découvrir des régularités dans les nombres premiers.

Depuis Legendre (fin du XVIIIe siècle), on sait que dans n'importe quelle suite arithmétique, il existe un nombre infini de nombre premiers ! (enfin, seulement quand le premier terme de la suite et la raison sont premiers entre eux, c'est à dire, n'ont pas de diviseurs communs).
Par exemple, premier terme 5, raison 7 : 5, 12, 19, 26, 33, 40, 47, 54, 61, 68, 75, ... Cette suite contient une infinité de nombres premiers !
Juste un petit a parte : selon le premier terme de la suite choisi, on aura soit 0 ou 1 nombre premier (si le premier terme et la raison ont un diviseur commun), soit une infinité de nombres premiers.

Ce qui est étonnant, c'est que dans ce deuxième cas, il y aura a peu près la même proportion de nombres premiers dans chaque sous-suite !

Petit exemple pour comprendre, avec la raison 6. Il y a une infinité de premiers lorsque le premier terme est 1 ou 5, et la proportion de premiers est à peu près la même dans ces deux suites :
0 - 6 - 12 - 18 - 24 - 30 - 36 - 42 - 48 - 54 - 60 - 66 - 72
1 - 7 - 13 - 19 - 25 - 31 - 37 - 43 - 49 - 55 - 61 - 67 - 73 -> 61%
2 - 8 - 14 - 20 - 26 - 32 - 38 - 44 - 50 - 56 - 62 - 68 - 74
3 - 9 - 15 - 21 - 27 - 33 - 39 - 45 - 51 - 57 - 63 - 69 - 75
4 - 10 - 16 - 22 - 28 - 34 - 40 - 46 - 52 - 58 - 64 - 70 - 76
5 - 11 - 17 - 23 - 29 - 35 - 41 - 47 - 53 - 59 - 65 - 71 - 77 -> 69%

Cela suffit-il pour se dire que les nombres premiers ne sont pas si mal rangés que ça ?
Peut-on aller plus loin et voir si cette proportion converge pour une suite arithmétique infinie ? Et si oui vers quelle limite ?

Klimrod · #22

ash00 a écrit:
Va falloir que je modère ce message en particulier !

J'avoue qu'à part Lui-meme et Nobodydy (mais ces deux-là, on ne les refera pas), mes petits camarades de jeux ont été plus sages que je ne le pensais.
Probablement qu'ils te craignent, maintenant !

nodgim · #23

Ash00, l'anti-trash qui ne laisse passer aucune tàche ?

nodgim · #24

@ Klimrod :
Ce Tao n'a t'il pas récidivé récemment en démontrant qu'il y a une infinité de couples de nombres premiers dont l'écart est inférieur à une valeur donnée (aujourd'hui, cette valeur doit être inférieure à 200, de mémoire) ?

aunryz · #25

à propos de ma demande relative à la suite
1 ; 12 ; 123 (concaténation des nombres de la suite des entiers)
"contient-elle des nombres premiers ?"

J'avais omis de regarder dans la bible (OEIS )
(http://oeis.org/A007908)
et je vois que (comme pour quelques autres ... heureusement pas toutes)
cette suite et la question qu'elle pose
a déjà été posé
et qu'un certain nombre de recherches ont abouti a

- en gros ce qu'on pense intuitivement [... mais rien n'est là pour le prouver]
à savoir qu'il devrait y avoir des nombres premiers dans cette suite
mais

- à ce jour pas de nombre premier dans les 200 000 premiers termes de la suite.

un commentaire qui résume

From: Neil Sloane [e-mail redacted to thwart site-scrapers]
Date: September 29, 2015 6:16:17 PM PDT
Subject: lovely open problem*

To Number Theory List,
Consider the sequence with nth term equal to the
concatenation of the decimal numbers 1234...n (
https://oeis.org/A007908)
When is the first prime? The comments in A007908 say
that there should be infinitely many primes, and that there
are no primes among the first 64000 terms.
If you would like to help with this search, you could leave a comment
in A007908 saying that there are no primes among terms X through Y,
or, of course, that n = Z gives a (probable) prime, which would be
pretty exciting.

Best regards
Neil
-----------

Bonne journée.

* Traduction : "un problème sexy" (sourire)

Forum dédié aux énigmes et à toutes formes de jeux de logique.	Déconnexion
Tu n'es pas identifié sur Prise2tete : s'identifier. Accueil Forum	[+]

#1 - 04-01-2017 18:43:28

Particularité de 017

#0 Pub

#2 - 04-01-2017 19:01:52

particulzrité de 2017

#3 - 04-01-2017 19:20:13

Particularté de 2017

#4 - 04-01-2017 20:13:04

Particualrité de 2017

#5 - 05-01-2017 00:01:59

Particulartié de 2017

#6 - 05-01-2017 09:45:57

paryicularité de 2017

#7 - 05-01-2017 09:53:27

paeticularité de 2017

#8 - 05-01-2017 10:03:46

particulzrité de 2017

#9 - 05-01-2017 10:45:44

Particularité e 2017

#10 - 05-01-2017 10:50:27

particularité se 2017

#11 - 05-01-2017 12:06:22

Particularité d e2017

#12 - 05-01-2017 13:58:44

particularité dr 2017

#13 - 05-01-2017 16:22:00

particilarité de 2017

#14 - 05-01-2017 19:43:35

Partciularité de 2017

#15 - 05-01-2017 19:51:47

particulatité de 2017

#16 - 05-01-2017 22:47:13

Partcularité de 2017

#17 - 06-01-2017 23:32:23

Particularité de 22017

#18 - 07-01-2017 21:27:23

particularité fe 2017

#19 - 07-01-2017 23:10:01

Paarticularité de 2017

#20 - 08-01-2017 01:05:31

Patricularité de 2017

#21 - 08-01-2017 08:36:31

Particularté de 2017

#22 - 08-01-2017 08:41:42

Partiularité de 2017

ash00 a écrit:

#23 - 08-01-2017 10:13:05

Particularité de 201

#24 - 08-01-2017 10:18:13

Particularité de 2071

#25 - 08-01-2017 10:42:13

Prticularité de 2017

Réponse rapide

Sujets similaires

Mots clés des moteurs de recherche

Pied de page des forums