 |
#1 - 01-02-2017 10:21:21
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Pavages eet chemins
Hello!


Hello!
Une question mathématique et un peu ouverte pour une fois, je n'ai pas la réponse.
Imaginez qu'on pave le plan, on le découpe donc en pavés, on est libre de le faire comme on le désire, de manière régulière, irrégulière, avec un seul type de pavé ou avec 500, tout est autorisé du moment que vous pouvez devenir/expliquer comment vous construisez votre pavage.
Si vous voyez votre pavage comme une plateau de jeu et les pavés comme des cases, vous remarquerez que souvent, le chemin le plus court entre deux cases (en nombre de cases adjacentes) n'est pas unique (il y a plusieurs trajets utilisant le même nombre minimum de cases à parcourir).
Et donc c'est la que réside mon interrogation du moment:
existe-t-il un pavage du plan qui garantisse qu'entre 2 pavés quelconques, le trajet le plus court en nombre de pavés adjacent soit unique?
Bonne chance!
#2 - 01-02-2017 11:14:00
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Pvaages et chemins
Quand tu franchis un noeud, ça compte pour combien ?
#3 - 01-02-2017 14:59:03
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Pvages et chemins
@nodgim: Tu es toujours sur une case (un pavé), tu ne te deplace que de case en case voisine (se touchant par un morceau de segment de longueur non nulle), et tu comptes 1 pour chaque case de ton chemin.
#4 - 01-02-2017 18:11:06
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Pavagse et chemins

Je pave avec des bandes infinies dans la direction verticale.
Si ma solution ne te convient pas, définis "pavé" 
#5 - 02-02-2017 08:22:51
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Paavges et chemins
ça me semble chaud à trouver, cette preuve !
En revanche, on peut facilement vérifier, pour un extrait de pavage ( une quinzaine de pavés groupés ) si ça marche ou pas.
On part d'un pavé qu'on numérote 0. Les voisins immédiats sont numérotés 1. Les voisins des voisins sont numérotés 2, les suivants 3, etc...
Il y a problème lorsque un pavé de numéro n+1 est en relation avec
au moins 2 pavés de numéro n.
La règle est donc simple. Mais trouver un groupement pour lequel ça marche pour chaque pavé numéroté 0 semble être une gageure....
#6 - 02-02-2017 10:19:40
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
pzvages et chemins
Bon je crois que j'ai la solution.
On représente chaque pavé par un point, et on relie chaque point par la relation de voisinage. On a ainsi un graphe. Le graphe est constitué de boucles à 2n ou 2n+1 points. Si 2n, c'est fini, car il existe 2 chemins d'égale longueur (nombre de points intermédiaires) reliant 2 points de la boucle. Si que des boucles 2n+1, 2 boucles voisines sont interconnectées par 2 points voisins ( c'est impossible de construire un pavage autrement). Dans ce cas, il existe une boucle supplémentaire réunisssant les 2 boucles, et donc comportant un nombre pair de points. Et donc 2 chemins d'égale longueur rejoignent 2 points opposés de cette boucle.
#7 - 02-02-2017 16:31:48
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Pavages et cehmins
On remarquera qu'on peut rechercher un "graphe planaire" et considérant que les nœuds symbolisent les paves et les arcs le voisinage de chaque pavé. Un graphe avec la propriété recherchée est dit "geodetic" . Il y a pas mal de mauvaises manières de répondre à ce problème, je n'en ai pas vu de bonne pour le moment.
#8 - 02-02-2017 16:46:12
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
pavages et chelins
Je ne comprends pas ta réponse. Dans ma tête, en tout cas, c'est très clair : 2 boucles max suffisent à trouver 2 chemins différents.
#9 - 02-02-2017 17:45:51
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Pavages et cchemins
Bonjour,
Voici ma réflexion pour l'instant:
Supposons que les pavés aient tous une taille bornée (sinon, c'est facile de trouver un pavage qui marche)
Considérons notre pavage comme un graphe planaire (un sommet par pavé, un arc entre eux si les pavés se touchent)
On peut déjà remarquer qu'une infinité de pavé touchent deux autres pavés au moins (sinon, on obtiendrait des cercles concentriques, et donc des pavés de taille aussi grande que souhaitée => pas borné)
De là, on peut déduire qu'étant donné deux points vérifiant cette propriété, on peut trouver un cycle passant par ces deux points.
Il est facile de montrer que l'on peut trouver un cycle de longueur paire, en effet deux cycles de longueur impaire se touchant forment un cycle de longueur paire.
Pour le construire, il suffit donc de prendre deux sommets A et B et trouver un cycle passant par eux deux. Si il est de longueur paire, c'est gagner, sinon, on prend un sommet C, et on cherche un cycle passant par B et C. S'il est de longueur impaire, le cycle somme des deux précédents cycles est de longueur paire.
on en déduit donc que l'on peut toujours trouver deux sommets tel qu'il existe deux chemins de même longueur les reliant (on les prends opposés sur le cycle de longueur paire)
Reste le problème du plus cours chemin:
On peut trouve un graphe planaire contenant un cycle paire (longueur 4) et tel qu'il n'existe qu'un seul chemin de longueur minimale: la clique d'ordre 4 (4 sommets reliés de toute les manières)
Or on peut trouver des cycles paire de taille aussi grande que l'on veut. Si l'on a un cycle pair de longueur 2n supérieure à 6, il faut que tous les sommets soient à moins de n-1 étapes
Après, je suis bloqué...
#10 - 02-02-2017 17:48:48
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
pavageq et chemins
nodgim, tu montres que tu peux trouver deux chemins de même longueur entre deux sommets, il reste à montrer que l'on peux les trouver minimaux...
#11 - 02-02-2017 17:51:57
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Pvages et chemins
On peut montrer avec une petite étude de cas qu'un graphe géodétique planaire infini ne peut pas contenir un cycle de taille 6. Si on montre ça pour toute taille paire supérieure à 6, c'est gagné...
#12 - 02-02-2017 18:09:30
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Pavages ett chemins
C'est sûr que, entre 2 pavés (points) il faut choisir les 2 boucles qui réunissent ces 2 points par le plus court chemin, mais l'existence de ce min est évidente !
#13 - 02-02-2017 18:13:28
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Pavages eet chemins
@nodgim : je ne comprends pas quand tu dis "2 boucles voisines sont interconnectées par 2 points voisins". Qu'est ce qui empêche que les deux points ne soient pas voisins, comme dans la figure ci-dessous, à gauche ?
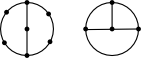
Mais ça ne change pas la conclusion de l'existence d'un cycle de longueur paire. Par contre, l'existence d'un cycle de longueur paire ne suffit pas à contredire l'unicité du trajet le plus court, cf la figure de droite.
@Clydevil : à tout pavage, on peut associer un graphe unique, si on considère qu'un graphe est la donnée abstraite d'un ensemble de sommets et d'arêtes (=des paires de sommets). Mais inversement, à un graphe, je peux associer plusieurs "pavages" différents. C'est pour ça que j'ai besoin que tu définisse ce que tu appelles "pavé" pour te répondre.
* un pavé doit-il être un polygone ?
* un pavé doit-il être d'aire finie ?
* un pavé doit-il être borné ?
* doit-il y avoir un nombre fini de pavés différents ? si oui, qu'appelle-t-on "différents" ?
#14 - 02-02-2017 18:22:06
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Pavaes et chemins
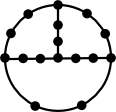
@caduk : voici un graphe géodétique contenant un cycle de taille 12.
#15 - 02-02-2017 18:41:39
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Paavges et chemins
Ebichu a écrit:@nodgim : je ne comprends pas quand tu dis "2 boucles voisines sont interconnectées par 2 points voisins". Qu'est ce qui empêche que les deux points ne soient pas voisins, comme dans la figure ci-dessous, à gauche ?
http://www.prise2tete.fr/upload/Ebichu-2figs.png
Mais ça ne change pas la conclusion de l'existence d'un cycle de longueur paire. Par contre, l'existence d'un cycle de longueur paire ne suffit pas à contredire l'unicité du trajet le plus court, cf la figure de droite.
@Clydevil : à tout pavage, on peut associer un graphe unique, si on considère qu'un graphe est la donnée abstraite d'un ensemble de sommets et d'arêtes (=des paires de sommets). Mais inversement, à un graphe, je peux associer plusieurs "pavages" différents. C'est pour ça que j'ai besoin que tu définisse ce que tu appelles "pavé" pour te répondre.
* un pavé doit-il être un polygone ?
* un pavé doit-il être d'aire finie ?
* un pavé doit-il être borné ?
* doit-il y avoir un nombre fini de pavés différents ? si oui, qu'appelle-t-on "différents" ?
Les configurations que tu représentes ne sont pas valables, il me semble. Mets les pavés par dessus, il me semble que ça ne marche pas.
Il y a une règle dont je n'ai pas parlé, je croyais ne pas en avoir besoin:
Une relation du graphe entre 2 sommets, avec des sommets intermédiaires, ne peut être "shuntée" par une relation extérieure qui oublierait des sommets. Si on représente un extrait du graphe, il manquera toujours les relations extérieures. Celles ci ne peuvent contourner les sommets sans aucune relation.
#16 - 02-02-2017 18:43:37
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Pavages et cehmins
Le graphe du msg 14 ne me semble par non plus valable. Les sommets intérieurs ne peuvent pas comporter seulement 2 liaisons, il en faut au moins 3 (triangle).
#17 - 02-02-2017 18:45:38
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Pavages et chemns
En matière de généralisation, j'avance que ce problème n'est pas plus compliqué avec des pavés biscornus, du genre géographie des pays. ça me rappelle beaucoup le problème des 4 couleurs.
#18 - 02-02-2017 19:02:18
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Pavages et chemin
Un sommet peut comporter 2 liaisons : cf Andorre coincée entre France et Espagne.
Pour le msg 14 : 
#19 - 02-02-2017 19:22:02
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Pavagges et chemins
Exact, je n'avais qu'à réaliser le découpage en pavés, ça m'aurait éviter de dire des c....
#20 - 03-02-2017 11:49:15
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
oavages et chemins
@Ebichu: Des elements de reponses tres interessants, si je n' ai pas repondu à tes questions sur la definition de pavé, c'est parceque le probleme est ouvert et que je pense que tu peux avoir l'intuition de l'esprit du truc, voir quelles contrainte ferait une meilleure solution qu'une autre. Il est également très difficile de de donner des contraintes qui élimineraient toutes les solutions "pathologiqued" faudrait pouvoir penser à tout, mais je peux te donner ce que mon intuition personnelle valorise comme contraintes (pas toute exclusives juste plus ou moins puissantes):
-Avoir une aire maximal de pavé.
-Avoir une aire minimal de pavé.
-Avoir tous les pavés plus petit (inclus) qu'un disque donné (une borne max)
-Avoir tous les pavés pouvant contenir un disque donné (une borne min)
-Avoir le moins possible de type de pavés.
-Avoir le plus possibles une structure régulière d' une manière ou d'une autre (que tous les paves d'un même type joue le même rôle, cf automorphisme du pavage etc...)
Enfin voila voila, beaucoup de contrainte libre de prendre ou de pas prendre mais qui ferait plus ou moins de notre pavage un pavage "normal et élégant" 
#21 - 03-02-2017 16:29:34
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Pavages t chemins
C'est bien ce que je craignais, tu es trop ambitieux 
Les graphes planaires géodétiques sont décrits depuis une thèse de 1964. Je n'ai pas accès à la thèse mais l'article suivant donne le résultat principal :
http://www.sciencedirect.com/science/ar … 0068800353
N'ayant pas la démo sous la main, j'en suis réduit à croire ce monsieur sur parole, mais il a l'air de dire que c'est assez long à démontrer.
Le résultat, si je comprends bien, implique qu'un graphe planaire géodétique est une arborescence dont les noeuds non triviaux sont soit un cycle impair, soit le graphe complet K4 éventuellement complété de quelques noeuds, comme dans le message #14.
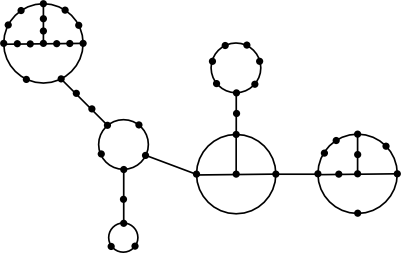
Ce type de structure ne permet pas d'obtenir de ce que tu accepterais de qualifier de "pavage"...
#22 - 03-02-2017 17:35:57
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Pavages et cehmins
@Ebichu: C'est tout le but de la question  savoir si j’étais ambitieux ou pas savoir si j’étais ambitieux ou pas  . Si la conclusion est exacte je trouve ça triste, en gros on a pas de discrétisation d' un espace de dimension 2 qui soit geodetic. . Si la conclusion est exacte je trouve ça triste, en gros on a pas de discrétisation d' un espace de dimension 2 qui soit geodetic.
Faudra que je lise l'article pour m'en convaincre car je suis en train d'imaginer une famille de trucs qui ne semble pas incluse et pour laquelle je ne vois pas comment ca peut "systematiquement merder" Supposons que tu prennes un grillage genre 4x4 = 16 noeud (maille carree). pour le moment ca marche pas (il y a beaucoup d'escalaier qui vont d' un noeud a un autre), mais je trouve cela bluffant qu'en inserant des noeud sur les segments (et donc en changeant de maniere non homogene le graphe) on puisse pas trouver de valeur qui marche. Mais ca doit etre liee a cette histoire de cycle minimal de longeur pair ou un truc dans le genre. A voir.
Merci!
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum













