|
#1 - 09-08-2015 20:50:47
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
#2 - 12-08-2015 16:14:12
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
chemins polynimiaux
Je vais commencer mes recherches, cependant j'aimerais que tu rajoutes du temps
Edit 1: Je pars sur une recherche à partir d'équations de droite
Un promath- actif dans un forum actif
#3 - 13-08-2015 00:29:41
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
cgemins polynomiaux
J'ai rajouté du temps !
@Promath- :
Spoiler : [Afficher le message]
C'est une bonne idée 
Je pense que le problème n'est pas si difficile. Il repose en fait sur une méthode mathématique surprenante que j'ai découvert récemment 
Je rajoute quelques indices dans l'énoncé.
#4 - 13-08-2015 08:51:35
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Chemins ppolynomiaux
Je dirais, comme ça au vu de ce qui se passe quand on fait tourner une droite autour du point départ, que l'arrivée n'est pas tjs accessible (sauf bien sûr si l'arrivée est sur le 2ème segment), mais que quand elle l'est, elle l'est par 2 chemins différents. En effet, à partir du 3ème segment, seule une partie de la droite qui prolonge ce segment est accessible. Et c'est pareil pour les suivants. Donc toute arrivée située sur les parties de droite (prolongeant les segments) accessibles peut être atteinte 2 fois.
#5 - 13-08-2015 10:05:14
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
chemins pomynomiaux
@nodgim:
Spoiler : [Afficher le message]
Tu as raison, dans certains cas il n'existe pas de chemin orthogonal de rang N-1 qui relie A et B 
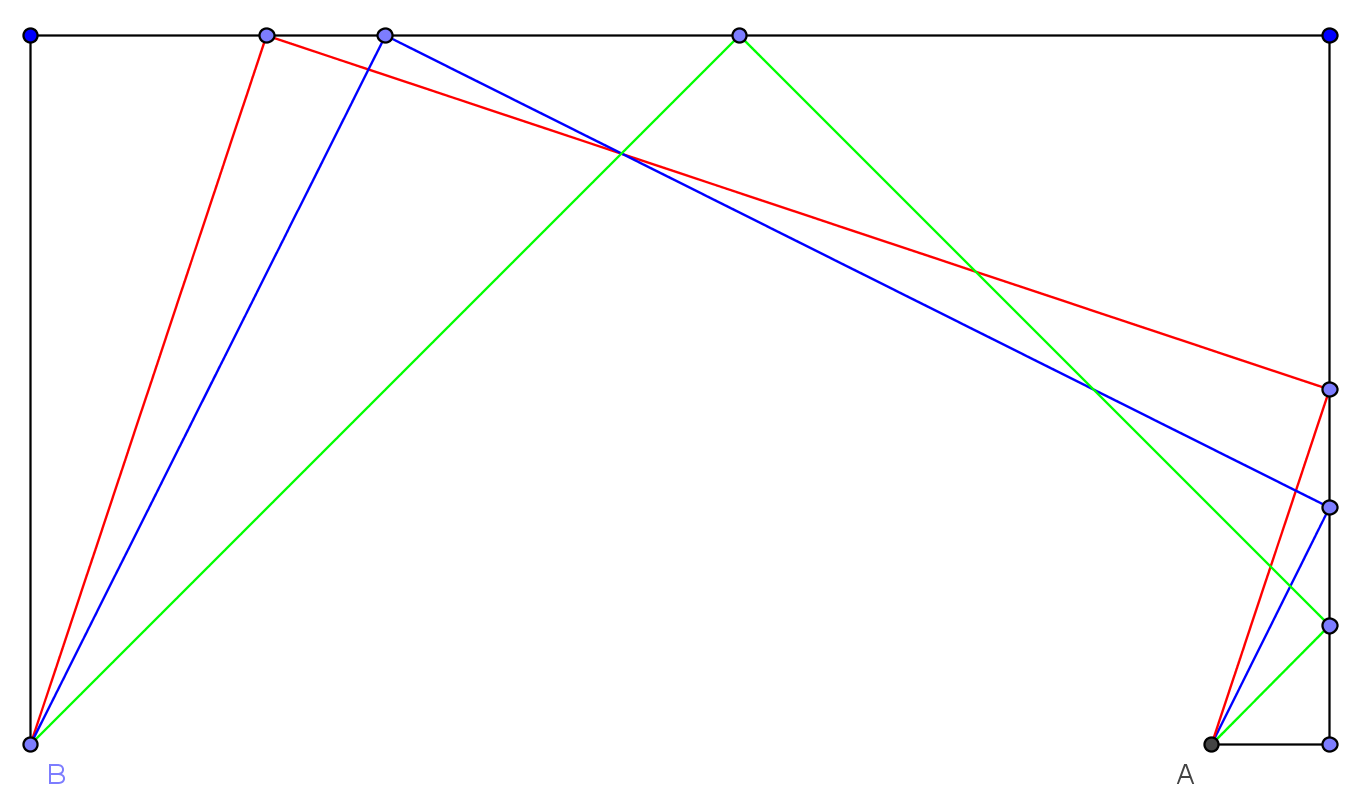
Par contre lorsqu'il en existe 1 il n'y en a pas forcément un 2ème pour autant ! Il peut aussi y en avoir plus de 2.
#6 - 13-08-2015 10:27:09
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
Chemins polynomiuax
Je conjecture le résultat suivant sans le démontrer pour le moment: il y a au maximum N-1 chemins de rang N-1. Dans chaque cas on aboutit à une équation polynomiale d'ordre N-1
Un promath- actif dans un forum actif
#7 - 13-08-2015 10:37:43
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
chemins polunomiaux
@ Promath- :
Spoiler : [Afficher le message]
Oui tout à fait !
Il ne doit pas te manquer grand chose pour conclure 
#8 - 13-08-2015 12:38:11
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Chmeins polynomiaux
Bonjour Sydre
Je n'ai pas participé au sujet parce que je n'avais pas compris la question et je ne suis toujours pas de l'avoir comprise .
Je résume à ma façon 
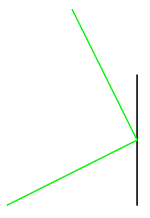
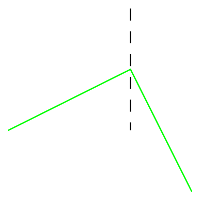
On a un réseau de droites numérotées de façon à ce que chacune soit perpendiculaire à sa précédente . On part d'un point A sur la première droite et on rejoint la deuxième selon le trajet de son choix . Ensuite il n'y a plus de liberté , on rejoint la deuxième droite perpendiculairement à la trajectoire précédente et ainsi de suite jusqu'au dernier point . On cherche de combien de façon on peut arriver au point B donné lui aussi sur la dernière droite .
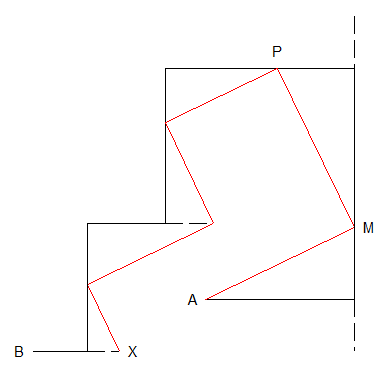
Il me semble que si on fait varier le point M sur son axe , le point P va faire un aller et retour de l'infini vers un des points ( c'est la projection d'une parabole ) . Le point P va générer le même phénomène sur son successeur .
A priori le nombre de solutions peut être aussi grand que l'on veut
Vasimolo
#9 - 13-08-2015 13:24:06
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
Chemnis polynomiaux
Hélas si puisque je peux démontrer pour les rangs faibles (3,4) mais pas pour tous les rangs en fait...
Un promath- actif dans un forum actif
#10 - 13-08-2015 14:05:46
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
chemins polynomiayx
@Vasimolo :
Spoiler : [Afficher le message]
Ta reformulation est tout à fait correcte 
Par contre je ne comprends pas comment tu trouves une infinité de chemins ?
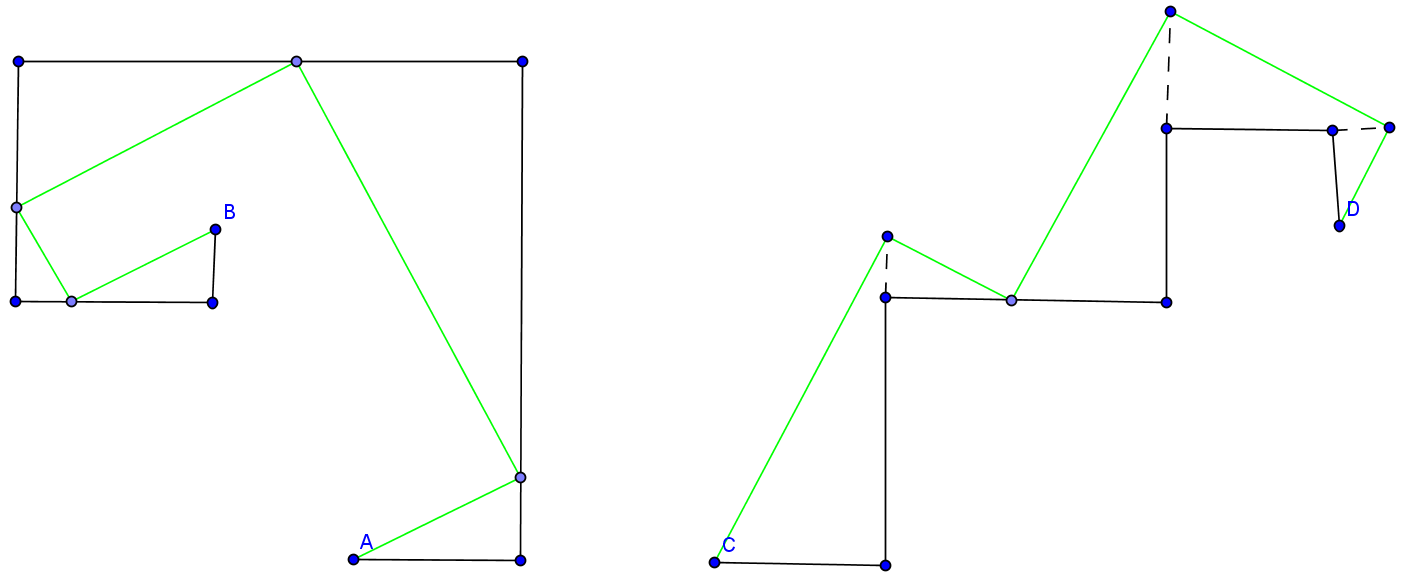
Par exemple pour ce chemin de rang 3 :

On ne peut pas construire de chemin de rang 2 reliant A et B !
@Promath- :
Spoiler : [Afficher le message]
Tu parlais dans ton précédent message d'une équation polynomiale de degré N-1.
Quelle est la condition sur ce polynôme pour que le chemin relie A et B ?
#11 - 13-08-2015 14:46:19
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
Cheminns polynomiaux
Qu'il ait une solution au moins, donc que ce polynôme soit de rang impair, donc un nombre N pair, mais ça c'est une propriété évidente car le premier segment tracé sera parallèle au dernier et comme on peut donner toutes les directions au premier le résultat en découle...
J'ai trouvé une autres solution, moins rigoureuse peut-être (je n'ai pas développé, si tu ne comprends pas je pourrai ajouter des phrases). Si certains signent disparaissent, c'est normal, puisque je ne parle pas de mesures algébriques mais de longueurs! Cela permet de conclure plus rapidement je pense

J'ai une autre idée qui consiste à partir sur une recherche d'équations avec des cercles, à voir!
C'est dingue comme les gens se jettent sur le problème dès qu'il reste peu de temps 
J'ai remarqué dans le dessin que tu as fourni qu'il y a une sorte de point où tous les chemins se croisent... Hasard?
Edit2: c'est un hasard effectivement
Un promath- actif dans un forum actif
#12 - 13-08-2015 16:48:50
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
chemins polynomizux
@Promath- :
Spoiler : [Afficher le message]
En fait les chemins possibles sont caractérisés par quelque chose de bien précis 
On peut s'en rendre compte via les équations de droites en se disant "Pour que mon chemin joigne A et B il faut et il suffit que le dernier segment de mon nouveau chemin, dont je peut calculer l'équation, passe par B" mais les calculs sont vraiment moches.
Il y a une autre caractérisation qui mène à des calculs beaucoup plus simples et qui porte sur l'évolution d'une certaine longueur dans certains triangles ...
#13 - 13-08-2015 18:05:18
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
Chemins poolynomiaux
"Il y a une autre caractérisation qui mène à des calculs beaucoup plus simples et qui porte sur l'évolution d'une certaine longueur dans certains triangles ..."
Ce n'est pas ce que j'ai évoqué dans la deuxième partie de ma feuille?
Édit:Lapidez moi! Comment je n'ai pas pu y penser plus tôt ! Les triangles sont semblables...
Un promath- actif dans un forum actif
#14 - 13-08-2015 18:23:49
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
chemins polynomizux
@Promath- :
Spoiler : [Afficher le message]
Non, tu n'as pas choisi le bon coté  Mais il en reste 2 autres ! Mais il en reste 2 autres !
L'idée est de trouver une relation entre une grandeur qui permet de caractériser le fait que le chemin relie A et B et une autre grandeur qui elle détermine de manière unique le chemin.
Edit : MàJ des indices !
#15 - 13-08-2015 19:13:53
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
chemind polynomiaux
Les triangles sont semblables, ça aide pas mal

Un promath- actif dans un forum actif
#16 - 13-08-2015 20:39:02
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
Chemins oplynomiaux
@Promath- :
Spoiler : [Afficher le message]
Ok ! Donc ta conclusion est qu'il y a autant de chemins que de racines réelles d'un certain polynôme 
Reste à trouver la forme générale du polynôme en question ...
Essaie avec la pente caractéristique du chemin au lieu de l'angle au sommet 
#17 - 14-08-2015 12:50:21
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
Chemins polynomiaaux
Mmh je ne vois pas ce que tu veux dire par pente caractéristique? Et ce n'est pas possible de trouver le polynôme avec l'équation que j'ai mise en haut de la feuille?
Un promath- actif dans un forum actif
#18 - 14-08-2015 14:22:14
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
Chemins polynomiaaux
Tout d'abord bravo à Promath- pour avoir répondu à la question 
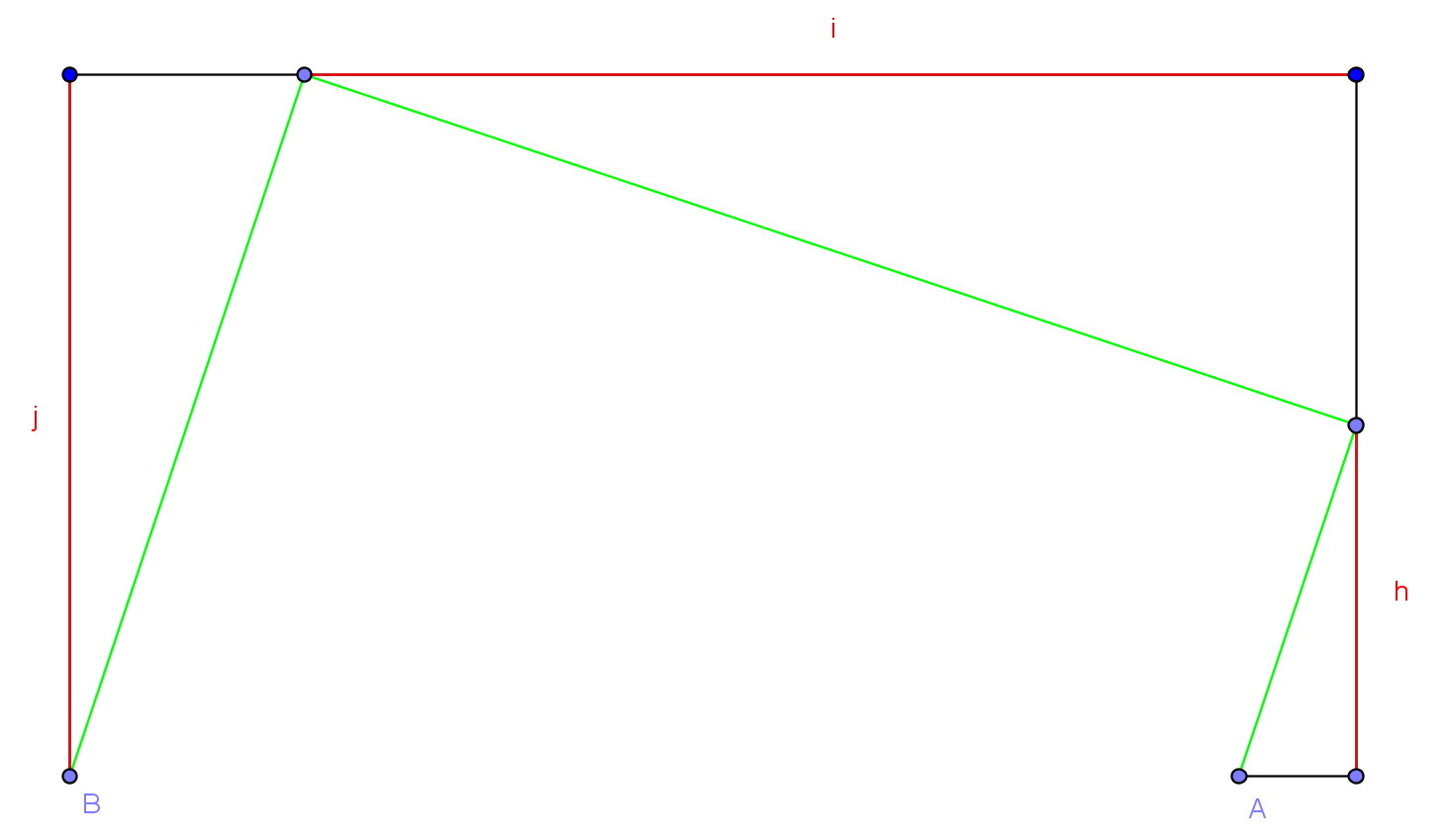
Le problème reposait en fait sur la méthode de Lill qui permet de déterminer graphiquement les racines d'un polynôme de degré quelconque.
Il y avait autant de chemins reliant A et B que de racines réelles du polynôme a(n)*x^n + a(n-1)*x^(n-1) + ... + a(0) ou les a(n) sont les longueurs des segments du chemin.
En fait, trouver un chemin revient à trouver une racine réelle du polynôme car la pente caractéristique p du chemin est solution (se démontre par un raisonnement analogue à celui de Promath-).
#19 - 14-08-2015 18:30:20
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
chrmins polynomiaux
Un très joli problème et une très jolie solution 
Il me semble qu'il y a quelques petites nuances à apporter à la solution . Le nombre de chemins est inférieur ou égal au nombre de racines réelles du polynôme . Les racines multiples ne donne qu'un seul chemin et certains chemins peuvent être un peu "dégénérés" ( voir le -0,5 pour 4x^3+2x^2-2x-1 sur le lien ) .
Heureusement que je n'ai pas cherché trop longtemps , je n'aurais jamais pensé à ça 
Vasimolo
|
 |
|
Prise2Tete
Forum
Statistiques
Liste des membres
Hall of Fame
Contact
|

 Accueil
Accueil
 Forum
Forum