 |
#1 - 19-04-2017 13:05:46
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Dominos et solitaier
Bonjour,
1) Considérons le quadrillage carré suivant, dont les côtés comportent un nombre pair de cases (quelconque), et dont les deux cases aux extrémités ont été retirées. Est il possible de recouvrir ce quadrillage de dominos?
Un domino occupe deux cases adjacentes, jamais en diagonale, ils ne se chevauchent jamais, et n'occupent jamais l'un des deux coins supprimés.
Un exemple de début de recouvrement est donné par les dominos rouges.

2) Considérons le jeu suivant:
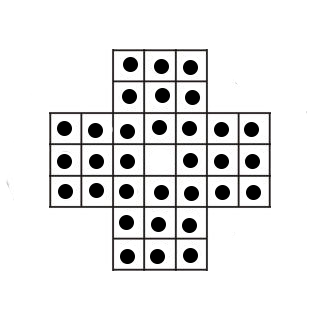
On dispose d'un plateau en croix tel que sur chaque case, il y a un pion, sauf sur la case centrale ou il a été retiré. A chaque étape, on déplace un pion au dessus d'un autre, de manière à manger le pion.
Un mouvement est valide si:
- Il y a deux cases adjacentes avec chacune un pion
- la case derrière ces deux pions est libre
Un pion ne peut en manger qu'un seul à la fois. Le pion mangé est retiré du plateau. Le pion mangeur est placé sur la case qui était vide. Les cases ou était le mangeur et le mangé sont désormais vide.
Un pion ne peut pas sortir des limites du plateau pour manger, les 3 cases concernées par un mouvement sont alignées, il ne peut jamais y avoir plus d'un pion sur la même case.
Voici un exemple de mouvement que l'on peut faire au tout début (c'est d'ailleurs le seul possible à la symétrie près)
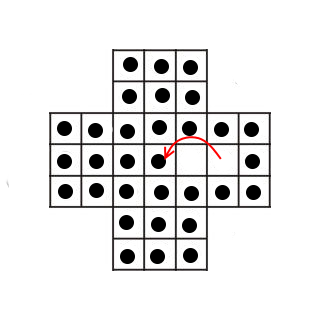
On remarque qu'à chaque mouvement, le nombre de pions sur le plateau diminue de un.
Le but est de manger tout les pions de manière à ce qu'il n'en reste plus qu'un (qui ne pourra évidemment plus manger). Lorsqu'il n'y a plus de mouvement possible, la partie est terminée (tout les pions sont isolés, ou si ils sont sur un même ligne, les extrémités de la ligne touchent les bords du plateau). Elle est gagnée s'il reste un pion, perdue si il en reste plusieurs (et vous avez triché s'il en reste zéro...  ) )
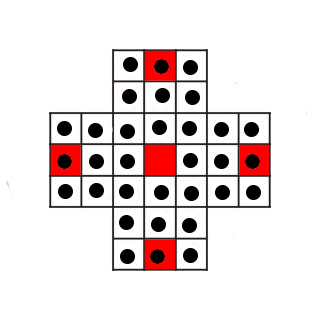
Démontrer qu'en cas de victoire, le pion gagnant ne peut se situer que sur l'une des cases en rouge.
#2 - 19-04-2017 15:48:20
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,193E+3
Domino et solitaire
Salut,
1 ) non, si on le colorie comme un échiquier il y aura autant de cases blanches que de noires, chaque domino recouvrant une case blanche et une case noire. Or les deux coins sont de la même couleur.
2 ) Je ne vois pas vraiment le rapport entre les deux problèmes... à part le coloriage :

A chaque tour, la parité des trois couleurs change, -1 pour la couleur d'où on part, -1 pour celle que l'on mange, +1 pour celle où on atterrit.
En 2 coups, la parité reste inchangée.
En 30 coups aussi, et donc, au bout de 31 coups, le dernier pion sera rouge. (seule couleur paire dès le départ.
Si on suit le même raisonnement selon les autres diagonales, il n'y a que tes 5 cases qui soient communes aux deux preuves de possibilités.

Ce sont d'ailleurs des positions dites "équivalentes" car on peut les obtenir à partir des mêmes cas de figure à 2 pions.
Au niveau des équivalences, un peu de lecture : http://eternitygames.free.fr/Bernard%20 … ire-v2.pdf
#3 - 19-04-2017 16:27:32
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
#4 - 20-04-2017 14:02:21
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
dominos et solitaure
Le premier est un classique. Si on considère un damier au lieu d'une grille, alors chaque domino couvre une case noire et une blanche. En enlevant 2 coins opposés, on arrive forcément à 2 cases noires de moins que de blanches (ou inversement) pour une taille de damier paire. Donc impossible de paver avec des dominos.
Pour le solitaire, je me rappelle vaguement d'une solution à base de classes d'équivalences : une case est paire ou impaire, le but est d'avoir une seule case impaire, 'manger' correspond à changer la parité de 3 cases consécutives.
De ce fait, puisqu'on peut paver le solitaire avec des briques 1x3, alors
- on peut le résoudre quelle que soit la case de départ : on change toutes les parités, qui valent 1 au départ sauf sur la case vide, reste une seule case paire, celle de départ
- s'il s'agit du centre, alors le centre est atteignable en fin de parcours.
- toujours d'après la même règle, toutes les cases à une distance 3 du centre sont atteignables (en ajoutant au pavage 2 briques supplémentaires, puisque [0 0 0 1] peut devenir [0 1 1 0] et enfin [1 0 0 0])
- et pour finir, les autres cases ne le sont pas puisque le système n'est alors pas équivalent au système de départ.
#5 - 20-04-2017 16:23:15
- Klimrod
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 4054
- Lieu: hébesphénorotonde triangulaire
Dominos et solitaie
Bonjour,
1. Damier :
Ce problème est classique et certainement déjà posé sur ce site.
Le plateau de jeu est constitué de cases blanches et noires alternées. Si l’on affuble les cases blanches de la lettre A et les cases noires de la lettre B, alors on ne pourra paver le plateau avec des dominos que si le nombre de cases A est égal au nombre de cases B.
Pour un plateau carré ou rectangulaire de longueur/largeur paires, le fait d’enlever les deux angles diamétralement opposés revient à enlever deux cases de même couleur. Il est donc impossible de le paver avec des dominos.
2. Solitaire :
On va utiliser la même numérotation, mais avec trois lettres A, B et C :
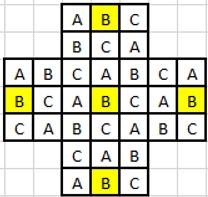
Au préalable, il faut remarquer qu’à chaque fois qu’on joue un coup, les trois cases impliquées sont des cases A, B et C, et qu’il s’agit d’enlever deux pions de deux cases différentes pour en ajouter un sur la 3ème case. En d’autres termes, si on s’intéresse aux parités du nombre de pions sur les cases A, sur les cases B et sur les cases C, à chaque coup, on inverse les trois parités.
Le plateau de jeu contient 33 cases A, 33 cases B et 33 cases C. Au départ, on enlève le pion central. Donc A=33=impair, B=32=pair et C=33=impair.
Puisqu’à chaque coup, on inverse les parités et qu’à la fin, on ne doit plus avoir qu’un seul pion, la seule position finale possible est A=0, B=1 et C=0.
Cela signifie que le pion final est nécessairement sur une case B.
Il reste encore à montrer que certaines cases B ne sont pas possibles.
Je reviens plus tard si j’arrive à creuser…
[Edit] Ah ben je suis bête... 
Comme le problème est symétrique et invariant par rotatipn de 90°, cela élimine de facto les cases B qui ne sont pas sur fond jaune.
Les cases B sur fond jaune sont donc les seules positions finales possibles.
Remarque : il faudrait encore montrer qu'il existe des parties permettant de finir sur ces cases jaunes...
 Klim. Klim.
J'ai tant besoin de temps pour buller qu'il n'en reste plus assez pour bosser. Qui vit sans folie n'est pas si sage qu'il croit.
#6 - 20-04-2017 16:29:56
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Domino et solitaire
1) Colorier les cases en noir et blanc comme sur un échiquier, chaque domino enlève alors une case de chaque couleur. Comme il n'y a initialement pas le même nombre de cases blanches et noires c'est impossible.
2) Sur chaque ligne on numérote les cases 011011011... puis la ligne suivante 101101101... et ainsi de suite en décalant d'un cran à chaque fois. La case centrale doit être numérotée 0. Chaque coup conserve la parité du nombre de 1. On en déduit que le dernier pion doit être sur une des 11 cases numérotées 0. On fait le raisonnement symétrique en décalant dans l'autre sens : on obtient 11 autres cases, et seules 5 cases sont dans les 2 ensembles de 11.
#7 - 20-04-2017 17:04:33
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Dominos et sollitaire
scarta
Je n'ai pas bien compris...
Je ne pense pas qu'il y ait besoin de briques dans la seconde question, la question sur les dominos était surtout pour ceux qui ne serait pas familier des raisonnement sur les classes d'équivalences et parité.
Ebichu et Klimrod
parfait
#8 - 23-04-2017 14:24:05
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Domnos et solitaire
Félicitation à ceux qui ont trouvé!
|
 |

 Accueil
Accueil
 Forum
Forum











