Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 16-07-2015 15:38:22
Mathématiques pour les nuls 5 (Surplomb de dominos)Bon comme je suis sympas on va jouer aux dominos aujourd'hui. Comme la résolution du problème en lui-même est assez compliquée, et que je n'ai pas encore la réponse du moins la démonstration pour le présent problème, je vous invite à laisser des traces de vos essais avec des photos de dominos par exemple. "L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#0 Pub#2 - 16-07-2015 15:52:13
Mathématiques pour les nuls 25 (Surplob de dominos)C'est pas tout neuf http://www.prise2tete.fr/forum/viewtopic.php?id=8380 #3 - 16-07-2015 16:01:36
Mathématiques pour les nuls 25 (Surplomb de dominosOn va faire comme dans ton dernier post, on va revoir les bases "L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline #4 - 16-07-2015 16:10:49#5 - 16-07-2015 16:37:38
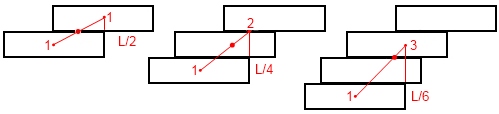
mathématiquzs pour les nuls 25 (surplomb de dominos)Chaque domino doit contenir la verticale du centre de gravité du paquet de ceux situés au-dessus de lui. Le raisonnement est plus facile si on construit la tour depuis le haut. #6 - 16-07-2015 18:36:12#7 - 16-07-2015 23:04:13
Mathématiques pour les nuls 25 (Surplomb de domino)sCette énigme me rappelle furieusement un empilage de briques que j'avais proposé (il y a déjà quelques années) ici : #8 - 16-07-2015 23:33:12
Mathématiques pour les nuls 25 (Surplomb dee dominos)Oui, je crois qu'on la déjà vue celle-ci Je ne vien sur se site que pour faire croir que je suis treise intélligens. #9 - 17-07-2015 00:01:43
Mathémtiques pour les nuls 25 (Surplomb de dominos)D'après la formule trouvée ici : http://prof.pantaloni.free.fr/IMG/pdf/S … riques.pdf (un raisonnement très bien expliqué !) la méthode proposée en photo avec 30 dominos donne un surplomb théorique maximal de 2 fois la longueur d'un domino. #10 - 17-07-2015 05:14:48
mathématiques pour les nuls 25 (sueplomb de dominos)
#11 - 17-07-2015 14:40:51
Mathématiques pour les nuls 25 (Surplobm de dominos)http://math.pc.vh.free.fr/divers/paradoxes/dominos.htm Un promath- actif dans un forum actif #12 - 17-07-2015 15:24:30
Mathématiques pour les nuls 25 (Surpplomb de dominos)Le surplomb maximum avec 30 dominos est de #13 - 17-07-2015 22:22:42
Matématiques pour les nuls 25 (Surplomb de dominos)Oh puis m**** j'enlève les heures et puis on va en reparler ensemble parce que moi même je comprends plus rien là "L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline #14 - 17-07-2015 22:42:14#15 - 18-07-2015 00:21:56
mathématoques pour les nuls 25 (surplomb de dominos)J'ai lu récemment un article de Jean-Paul Delahaye qui traitait ce problème : "Surplombs maximaux" . L'exercice est vraiment complexe et je ne suis pas sûr qu'un site d'énigme soit le meilleur endroit pour en débattre . #16 - 18-07-2015 01:05:25
Mathématiques pour ls nuls 25 (Surplomb de dominos)Quand je dis parlons, je dis parlons de ce que nous avons à proposer, le problème semble encore être ouvert d'après cet article (en anglais) trouvé par hasard : maximum overhang "L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline #17 - 18-07-2015 07:43:35#18 - 18-07-2015 11:37:31
Mathématiques pour ls nuls 25 (Surplomb de dominos)Bravo à vasimolo qui a le premier pointé vers ma propre énigme d'il y a 4 ans
Ils ont dû faire chacun une (ou deux) erreurs de calcul ! Par exemple de s'arrêter à 29 ou/et de diviser par 2 ?
Je trouve au contraire qu'il devient évident quand on a compris qu'il fallait commencer le calcul itératif par le haut de la pile et qu'il a donc parfaitement sa place ci #19 - 18-07-2015 12:29:21#20 - 18-07-2015 15:48:59
Mathématqiues pour les nuls 25 (Surplomb de dominos)Au temps pour moi Réponse rapideSujets similaires
Mots clés des moteurs de recherche
|
 | |||||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | |||||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.






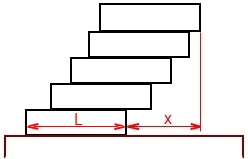 était beaucoup moins explicite que ta photo qui indique déjà clairement la solution.
était beaucoup moins explicite que ta photo qui indique déjà clairement la solution.
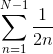 planche(s).
planche(s).