 |
#1 - 09-12-2017 13:06:15
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Des nombres premiers inégalement épartis ?
Bonjour @ tous.
Les nombres premiers autres que 2 ou 3 sont de la forme 6k-1 ou 6k+1.
Après observation des n premiers nombres premiers, vous direz si l'une ou l'autre des 2 catégories 6k-1 ou 6k+1 est la plus représentée.
Si vous y voyez une tendance majoritaire pour l'une ou l'autre, vous tenterez d'en expliquez la raison.
Bonne recherche.
PS: sujet effacé par manque de réaction puis réécrit à la demande d'un PTnaute. C'est un sujet difficile, comme tous ceux qui abordent les nombres premiers, et cette question particulière pourrait être activée des années durant...
#2 - 09-12-2017 17:47:50
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
Des nombres premiers ingalement répartis ?
On note
[latex]f_1(n)[/latex] le nombre des n premiers nombres premiers (2 et 3 exxclus) de la forme 6k-1.
[latex]f_2(n)[/latex] le nombre des n premiers nombres premiers (2 et 3 exxclus) de la forme 6k+1.
Il semble que l'on ait toujours [latex]f_1(n) > f_2(n)[/latex] . Encore faudrait-il le prouver...
De plus il semble que [latex]f_1(n) - f_2(n)[/latex] soit "de l'ordre" de la racine cubique de n ; à un facteur près voisin de 1 mais augmentant lentement avec n.
#3 - 10-12-2017 08:19:17
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
des nombres premiers inégakement répartis ?
@ Masab:
Je suis d'accord avec toi sur le groupe majoritaire, mais pas sur ton estimation d'écart. Cela dit, tu as dû établir un petit programme pour le comptage, ça m'intéresserait d'avoir des données pour des nombres assez grands, par l'exemple de l'ordre de 10 ^5 ou 10^6. ça me permettrait de me conforter dans mon estimation théorique.
Nota: les fluctuations sont importantes pour les nombres de l'ordre du 10^3, ça m'intéresse beaucoup de savoir si c'est aussi fort pour les grands nombres.
#4 - 10-12-2017 09:59:15
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
Des nombres premiers inégaalement répartis ?
Voici des résultats jusqu'au million des premiers nombres premiers.
[TeX][n, f_1(n)-f_2(n), 2\sqrt[3]{n}][/TeX]
Les résultats sont mis pour n variant par sauts de 10000 ; pour le 3ème composant, on indique la partie entière.
[10000, 22, 43]
[20000, 34, 54]
[30000, 60, 62]
[40000, 44, 68]
[50000, 86, 73]
[60000, 82, 78]
[70000, 66, 82]
[80000, 68, 86]
[90000, 74, 89]
[100000, 76, 92]
[110000, 152, 95]
[120000, 140, 98]
[130000, 80, 101]
[140000, 90, 103]
[150000, 126, 106]
[160000, 94, 108]
[170000, 100, 110]
[180000, 94, 112]
[190000, 104, 114]
[200000, 116, 116]
[210000, 172, 118]
[220000, 144, 120]
[230000, 192, 122]
[240000, 124, 124]
[250000, 112, 125]
[260000, 168, 127]
[270000, 190, 129]
[280000, 234, 130]
[290000, 252, 132]
[300000, 210, 133]
[310000, 112, 135]
[320000, 112, 136]
[330000, 142, 138]
[340000, 156, 139]
[350000, 128, 140]
[360000, 96, 142]
[370000, 84, 143]
[380000, 108, 144]
[390000, 96, 146]
[400000, 128, 147]
[410000, 156, 148]
[420000, 208, 149]
[430000, 220, 150]
[440000, 192, 152]
[450000, 204, 153]
[460000, 268, 154]
[470000, 252, 155]
[480000, 286, 156]
[490000, 276, 157]
[500000, 284, 158]
[510000, 252, 159]
[520000, 236, 160]
[530000, 156, 161]
[540000, 222, 162]
[550000, 236, 163]
[560000, 246, 164]
[570000, 260, 165]
[580000, 204, 166]
[590000, 190, 167]
[600000, 152, 168]
[610000, 226, 169]
[620000, 176, 170]
[630000, 168, 171]
[640000, 214, 172]
[650000, 212, 173]
[660000, 222, 174]
[670000, 202, 175]
[680000, 136, 175]
[690000, 198, 176]
[700000, 200, 177]
[710000, 124, 178]
[720000, 128, 179]
[730000, 132, 180]
[740000, 118, 180]
[750000, 254, 181]
[760000, 284, 182]
[770000, 280, 183]
[780000, 216, 184]
[790000, 268, 184]
[800000, 262, 185]
[810000, 290, 186]
[820000, 248, 187]
[830000, 206, 187]
[840000, 176, 188]
[850000, 314, 189]
[860000, 282, 190]
[870000, 338, 190]
[880000, 252, 191]
[890000, 328, 192]
[900000, 252, 193]
[910000, 282, 193]
[920000, 256, 194]
[930000, 252, 195]
[940000, 326, 195]
[950000, 260, 196]
[960000, 248, 197]
[970000, 306, 197]
[980000, 312, 198]
[990000, 360, 199]
[1000000, 340, 200]
#5 - 10-12-2017 12:01:30
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
des nombres premiers ibégalement répartis ?
Sur le premier million de nombres du type 6k-1, il y en a 206502 qui sont premiers.
Sur le premier million de nombres du type 6k+1, il y en a 206345 qui sont premiers.
Avec cette première approche, l'écart n'a pas l'air franchement significatif.
#6 - 10-12-2017 12:12:33
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
des nombres premiers inégalement répattis ?
@ Masab: merci pour ces données. Les résultats sont en moyenne plus forts que le minimum auquel je m'attendais.
@ Ebichu: c'est sûr que, en proportion, l'écart n'est pas significatif. En revanche, en données absolues, il est toujours du même coté et régulièrement croissant. C'est précisément sur cet aspect que la question est posée.
#7 - 10-12-2017 12:25:15
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
des nomnres premiers inégalement répartis ?
Sur ce premier graphique, je détermine pour les 10000 premiers couples (6k-1;6k+1) l'avance que prennent les nombres premiers du type 6k-1 sur ceux du type 6k+1. C'est-à-dire que le point le plus à droite du graphique montre qu'entre 5 et 60001, il y a 27 nombres premiers de plus de la forme 6k-1 (il y en a en réalité 3041, contre 3014 du type 6k+1).
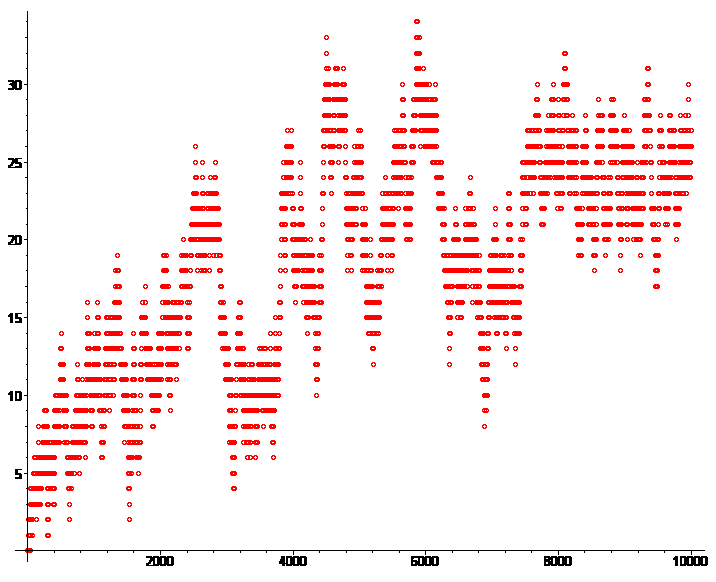
La même chose pour les 100000 premiers couples (je ne représente qu'un point sur 10 sinon mon ordi rame) :
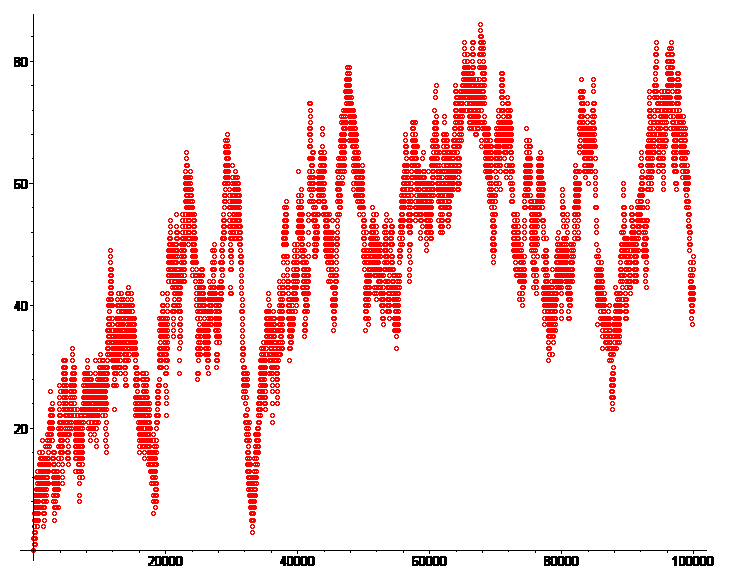
Ce n'est pas si net que 6k-1 a un avantage à long terme. Ça ressemble beaucoup à une marche aléatoire sur Z, je trouve. Et on voit que vers 6*33000, on n'est pas loin d'une inversion.
#8 - 10-12-2017 13:54:11
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
des nombres premiers inégalement répartid ?
La même chose pour 1 million puis 10 millions :
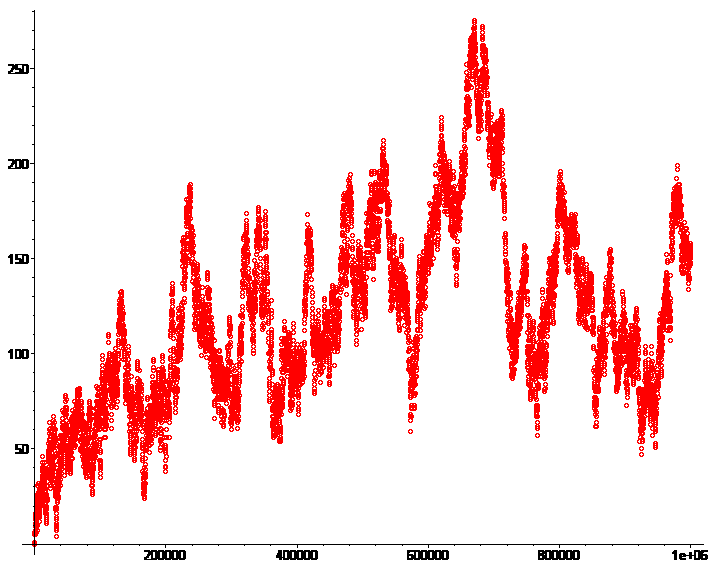
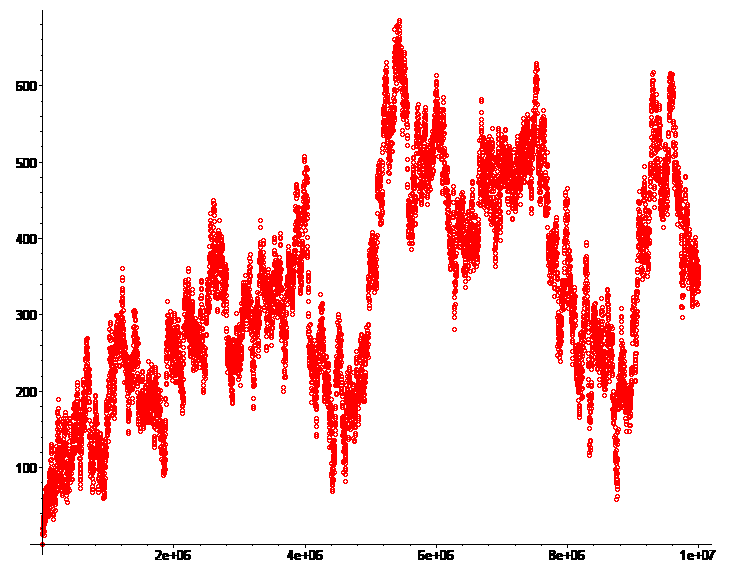
#9 - 10-12-2017 17:21:43
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
Des nombres premiers inégalement réparits ?
Bonjour,
Voici quelques résultats, pour comparer (le numéro d'ordre inclut les nombres 2 et 3).
#10 - 10-12-2017 18:27:26
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Dse nombres premiers inégalement répartis ?
Merci Ebichu pour tes graphiques édifiants et Enigmatus pour tes données.
@ Ebichu : ce qui me frappe dans tes 4 graphiques, c'est qu'en changeant d'échelle, le graphique ne change pas de forme générale. Je ne m'attendais pas du tout à des pics vertigineux dans un sens ou dans l'autre, mais je n'excluais pas non plus cette possibilité. Toutefois, je pense qu'une inversion est peu probable bien que théoriquement possible.
#11 - 10-12-2017 18:57:40
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
des nombres premiers inégalement eépartis ?
Ça me rappelle https://fr.wikipedia.org/wiki/Nombre_de_Skewes : s'il faut aller jusqu'à 1,39822×10³¹⁶, mon ordinateur n'est pas près d'observer une inversion 
#12 - 10-12-2017 19:58:20
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Des nombrs premiers inégalement répartis ?
@ Ebichu : Je connaissais cette histoire. C'est surprenant ce que les esprits les plus puissants peuvent découvrir dans le fin fond des choses...
A contrario de ce que j'ai annoncé dans le mail précédent, l'inversion est effectivement possible pour les très grands nombres. ça ne remet pas en cause ma petite idée initiale sur le sujet, ça la conforte même, j'en prends conscience maintenant.
Indice: Parfois, il faut compter en creux, non pas les présents, mais les absents.
#13 - 11-12-2017 10:50:07
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
Des nombres premiers inégalement réparttis ?
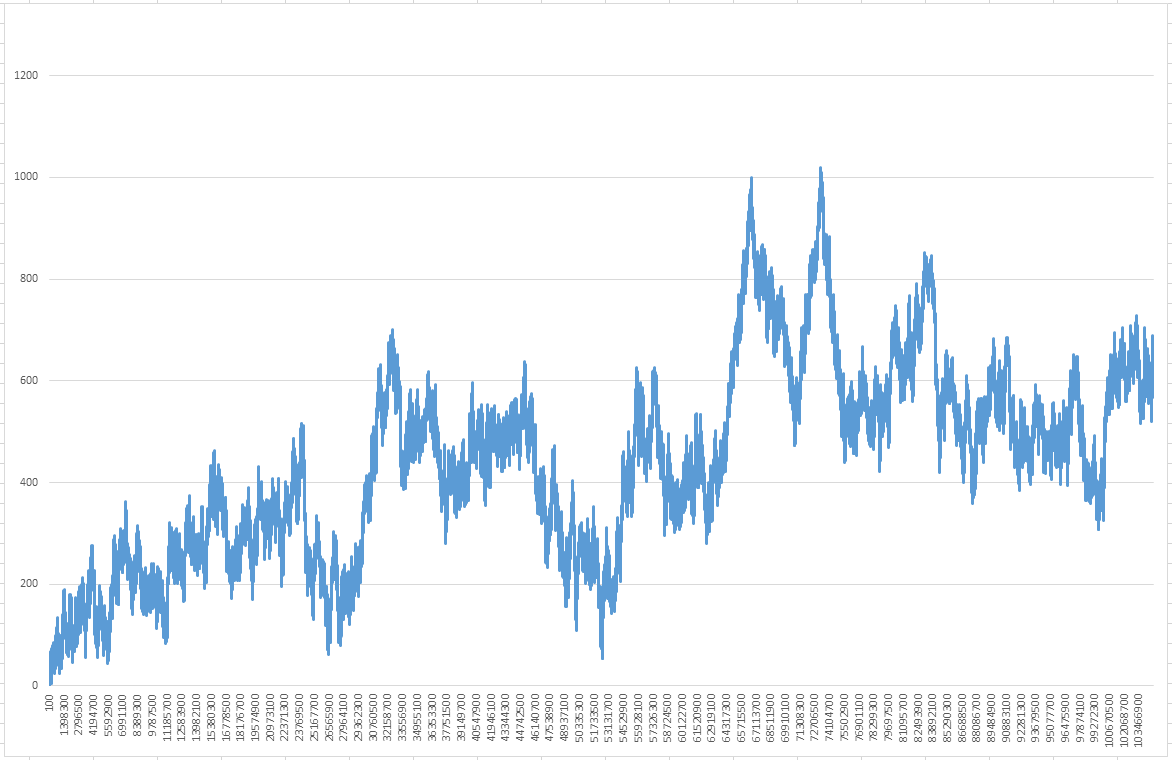
Mesure toutes les centaines, jusqu'à 104857600 - merci Excel et ses 1.048.576 lignes max 
#14 - 11-12-2017 11:35:18
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Des nombres premiers ingalement répartis ?
Et maintenant Scarta qui nous fournit un graphique jusqu'à 100 millions !
Avec EXCEL s'il vous plait. Je n'aurais pas imaginé que ce logiciel puisse fournir ce genre de données, je voyais bien l'obligation d'une routine quelque part. A moins que EXCEL n'ait servi que pour le graphique ?
Merci en tout cas pour ce travail.
#15 - 11-12-2017 15:09:56
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
des nombres premiers inégalement tépartis ?
Oui c'est du c# qui fait le calcul (3 secondes environ + 1.5 secondes pour générer un fichier CSV) et le graphique arrive ensuite
#16 - 11-12-2017 17:14:39
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
ded nombres premiers inégalement répartis ?
Pffff....3 secondes pour calculer ces données + 1,5 seconde pour les sortir.
Dire qu'il y a un siècle, une vie d'homme, et même de plusieurs, n'aurait pas suffit....
#17 - 12-12-2017 09:23:59
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
Des nombbres premiers inégalement répartis ?
L'algo utilisé date de 2.200 ans quand même...
#18 - 12-12-2017 17:37:22
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Des nombres premiers ingalement répartis ?
L'idée que j'en ai sur ce sujet est assez basique: elle part du principe que le plus petit multiple d'un nombre composé de facteur p est p² et que p² est toujours un 6k+1.
Pour tenter d'exprimer cette possible différence, on peut raisonner ainsi :
Tout nombre de la forme 6 k + / - 1 est un produit de 1 ou 2 nombres 6 k + / - 1. Si c'est le produit d'un seul de ces nombres, alors c'est un nombre premier, sinon c'est un nombre composé.
Soit N un nombre donné dont on veut connaitre la différence entre le cardinal des nombres premiers 6k - 1 et celui des 6k + 1.
En faisant [N/6] on obtient le nb de couples 6k + / - 1, le dernier pouvant être tronqué dans le cas où N = 0 ou -1 modulo 6.
On suppose au départ que tous ces couples sont premiers, et on va tenter de compter ceux qu'il faut éliminer. En identifiant un nombre composé et son signe (+ pour 6k+1, - pour 6k-1), et en les comptant, on peut par soustraction retrouver les nombres premiers + et -.
La plus élémentaire des méthodes consiste à dénombrer les produits de 2 de ces nombres, quitte à corriger les redondances après coup.
On procède ainsi pour les produits, toujours le plus petit nombre 6k+/- 1 facteur commun :
5*5, 5*7, 5*11, 5*13...jusqu'à 5 * [N/5], [N/5] étant en fait le 6k +/- 1 le plus près de [N/5].
7*7, 7*11, 7*13, 7*17....jusqu'à 7 * [N/7]
11*11, 11*13, 11*17,....jusqu'à 11* [N/11]
etc...jusqu'au dernier nombre qui sera le (6k+/-1)² le plus proche de N.
En matière de signe de ces différents nombres composés, ça donne :
+ - + - + - + - ....pour 5
+ - + - + - + - ...pour 7
+ - + - + - + - ...pour 11
etc...
Comme chaque série est une alternance de "+" et de "-" qui commence toujours par "+" :
- il ya autant de nombres composés "+" ou "-" si la série se termine par "-".
- il y a 1 nombre composé "+" surnuméraire si la série se termine par "+".
Dans le bilan moyen Bm d'un N donné, parmi les V(N) / 3 séries, il y en aura en moyenne 2/3 nombres composés "+" surnuméraires. En effet, pour les nombres 1 à 4 modulo 6, le plus grand 6k+/-1 en dessous est un 6k+1, et pour les nombres 0 ou 5 modulo 6, le plus grand 6k+/-1 en dessous est un 6k-1. Donc les surnuméraires "+" sont en moyenne de (2/9) * VN. Ce qui donne une supériorité égale de nombres premiers 6k-1.
On peut affiner ce (2/9)VN en remarquant que les séries ayant comme tête un nombre composé est inutile. (2/9) VN / ln (VN) est donc plus juste pour N un peu plus grand.
Mais ce mode de calcul est à corriger par les doublons, les triples, les quadruples, etc....dûs aux décompositions multiples, et pas seulement binaires, des nombres composés. Une approche analytique des différents cas possibles ne permet pas de dire si ces corrections sont en faveur des "+" ou des "-". Ce qu'on peut dire, c'est que les décompositions uniquement binaires des nombres composés, à savoir le produit de 2 nombres premiers, diminuent en proportion, avec l'accroissement de N, vis à vis des décompositions triples, quadruples, etc..Et que donc la moyenne fixée est de moins en moins fiable plus N est élevé.
#19 - 13-12-2017 16:32:20
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
des nombres premirrs inégalement répartis ?
@scarta : peux-tu partager ton code ? J'aimerais voir, avec un peu plus de 3 secondes de temps de calcul, s'il est possible d'observer une inversion, c'est-à-dire un moment où les nombres du type 6k+1 passent devant. Mais vu la rapidité de ton programme, je suppose qu'il sature vite la RAM ?
#20 - 13-12-2017 20:05:50
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
Des nomrbes premiers inégalement répartis ?
Salut,
J'ai testé les [latex]10^{10}[/latex] premiers couples [latex](6k-1;6k+1)[/latex] : pas d'inversion.
@scarta : Je suis curieux de savoir comment tu fait pour tester la primalité aussi vite ; en utilisant une implémentation de Miller-Rabin en C# j'en ai eu pour bien plus longtemps ...
#21 - 14-12-2017 10:38:06
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
Des nombres premiers inégallement répartis ?
J'envoie mon code dès que je l'ai sous la main.
Mais bon dans l'absolu c'est :
-un crible jusqu'à 60.000.000 en stockant les premiers
-jusqu'à 120.000.000 j'ai décalé le crible.
Techniquement on peut monter jusqu'à 3.6E15 sans stocker un seul premier supplémentaire. Mais là ça va devenir long (~ 1 seconde par tranche de 60 millions, ça paraît peu, mais pour atteindre la limite il faut... 1 million de minutes)
#22 - 14-12-2017 11:27:55
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
Des nombres preemiers inégalement répartis ?
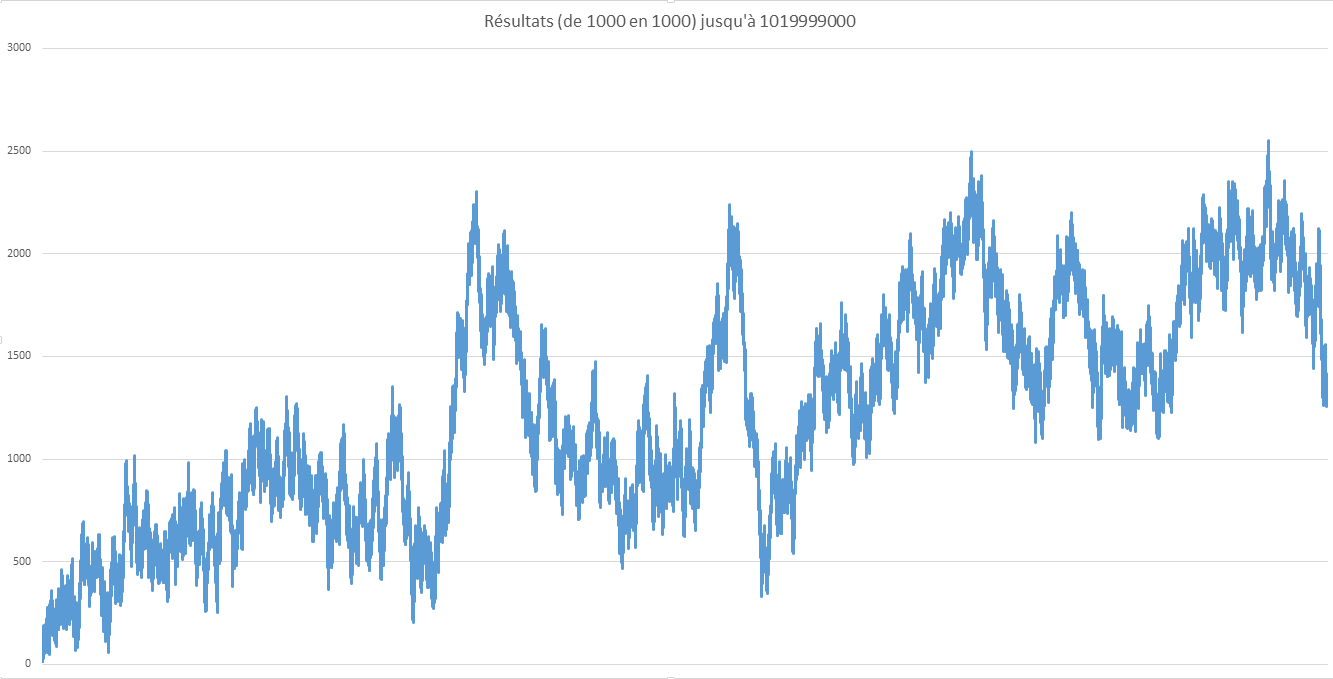
Voilà le code et un nouveau graphe jusqu'au milliard (~39.7secondes)
#23 - 14-12-2017 13:21:31
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
Des nombres premiers inégaement répartis ?
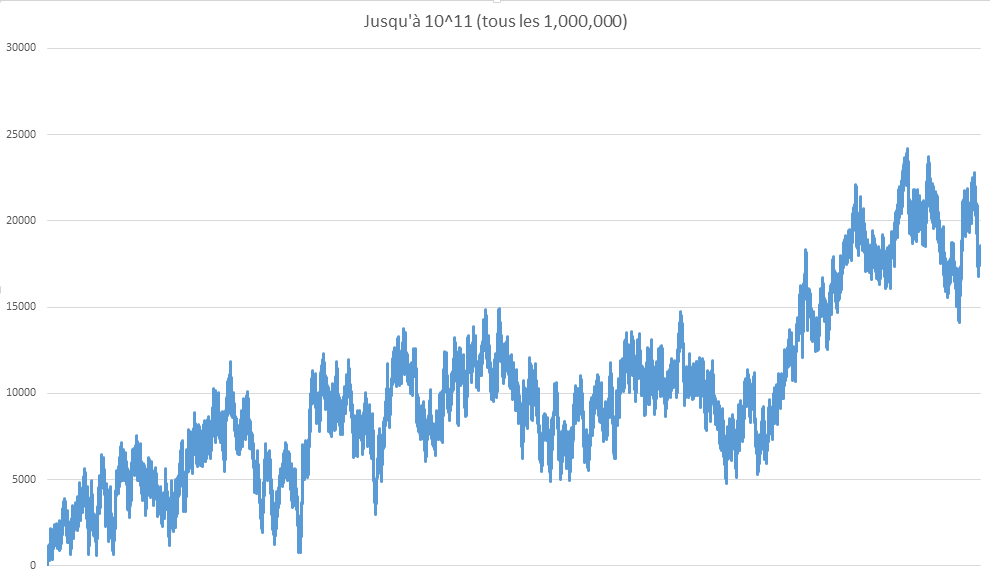
Et en 1h20
#24 - 14-12-2017 18:47:53
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Des nombres premiers inégalement répartiss ?
Merci Scarta pour ces nouveaux graphes !
On pourrait presque tracer une ligne droite pour la moyenne.....
#25 - 14-12-2017 19:15:53
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
des nombres premiers inégalrment répartis ?
Au vu du dernier graphe de Scarta, qui monte jusqu'à 10 ^ 11, on a l'impression de compter les carrés des nombres premiers inférieurs à N !
Le nombre de carrés de nb premiers jusqu'à N est donnée par la formule VN/ln(VN).
Pour 10^11, on obtient 24970, ce qui est assez proche de ce qu'on observe sur le graphe.
C'est comme si le carré d'un nombre premier prenait une place dans la suite des 6k+1 et qu'il la gardait infiniment. Les décalages se cumulent au fur et à mesure que ces carrés se découvrent.
|
 |

 Accueil
Accueil
 Forum
Forum













