Hello les gens!

C'est le moment de sortir un peu ses neurones. Votre job c'est de stocker des objets!

Supposons un instant que je vous donne une bande de cases et que je vous demande de stocker des objets parmi 2 types, A et B, tout en stockant de manière continue sur cette bande les objets d'un même type. Une évidence arrive à l'esprit pour bien faire les choses: disposer un des types à un extrémité de la bande, l'autre de l'autre coté et remplir l'espace progressivement par les 2 bouts, au fur et à mesure des arrivées, pour finir optimalement avec la bande remplie à la fin avec tous les objets d'un type d'un coté et ceux du second type de l'autre.



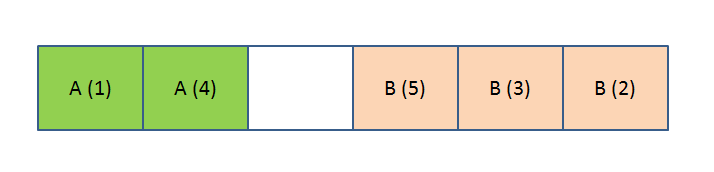
Et la ce qu'on va se demander, c'est comment se passent les choses avec plus de 2 types! On a qu'à dire des objets de uniquement 3 types: A B et C.

On vous file à la chaîne de tels objets et vous ignorez le nombre et l'ordre d'arrivée de chaque type: ça peut être uniquement des A ou une alternance de B et C par exemple.

Vous avez un espace de stockage, ie un ensemble de cases, certaines adjacentes entres elles (Un graphe quoi pour les intimes).
Une case stocke un objet et un seul, elle devient inutilisable après. Lorsqu'on stocke un objet on est obligé, si son type est déjà présent quelque part, de le stocker sur une case qui touche une case contenant un des ces précédents semblables. Ie l'espace de stockage dédié à un type en particulier est connexe à tout instant.

On considère que vous êtes bon, si, quelque soit l'ordre d’arrivée des objets, vous
ne pouvez plus suivre ces règles QUE dans le cas ou il n'y a plus du tout de place. C'est à dire que si votre espace n'est pas plein vous devez pouvoir accueillir des objets de n'importe quel type en leur assurant d’être voisins avec les objets du même type déjà présent.

Votre job est de concevoir, pour 3 types d'objets A, B et C:
- votre espace de stockage
- sa stratégie d'utilisation

Pour le moment il s'agit d'un problème assez ouvert alors il n'y a pas de restrictions, mais j'ai personnellement les préférences suivantes:

1) Quid d'un réseau de cases identiques pouvant être dessiné sur le plan (les voisins étant les cases qui se touchent) Y a t il un solution pour un nombre arbitrairement grand de cases au total?

2) Si 1 est impossible, quid d'un graphe planaire? (c'est moins contraignant car on peut déclarer voisin des cases pourtant physiquement très éloignées les unes des autres)

Et toute caractérisation intéressante est la bien venue!

Bonne chance!