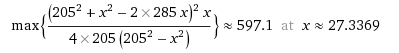Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 04-04-2011 11:30:02
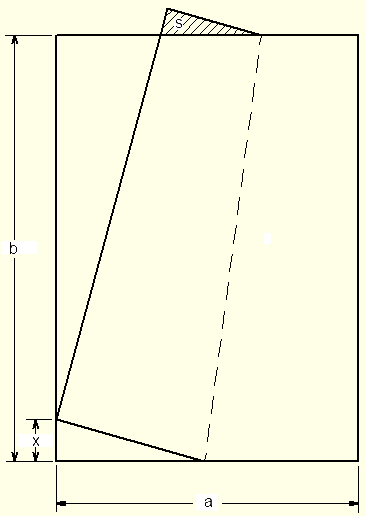
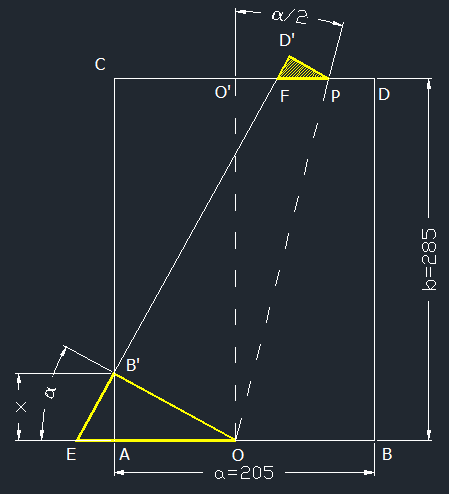
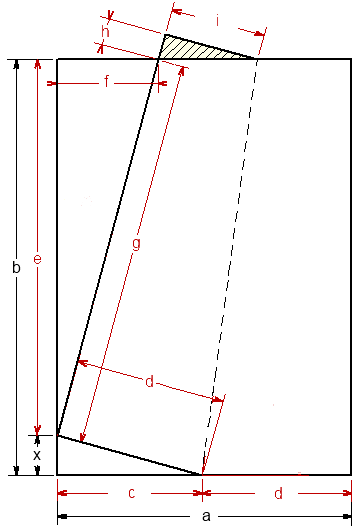
Pliage - marque e pagePour marquer les pages de mon magazine préféré, sur lesquelles je compte revenir plus tard, je ramène le coin bas-droit sur la pliure du magazine de manière à obtenir une surface visible dépassant en haut de la page.
#0 Pub#2 - 04-04-2011 13:27:36
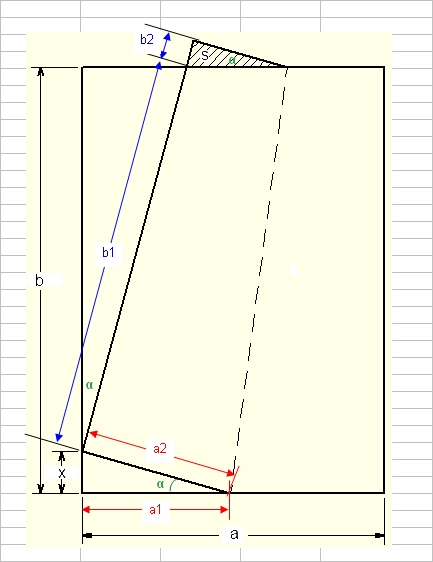
pkiage - marque de pageAvec un peu de Pythagore et de tangentes, je trouve : #3 - 04-04-2011 16:07:29#4 - 04-04-2011 17:07:21
Pliage - mraque de pageLe pli est la médiatrice du segment qui relie le coin quitté et la nouvelle position du point. #5 - 04-04-2011 17:13:15#6 - 05-04-2011 23:31:02#7 - 06-04-2011 08:35:22
pliage - marque fe pageBonjour Il aurait pu pleuvoir, con comme il est ! (Coluche) #8 - 06-04-2011 19:43:00#9 - 07-04-2011 21:46:35#10 - 07-04-2011 23:31:19
Pliage - marque de pageeLa surface S est The proof of the pudding is in the eating. #11 - 08-04-2011 09:13:33#12 - 08-04-2011 11:31:29
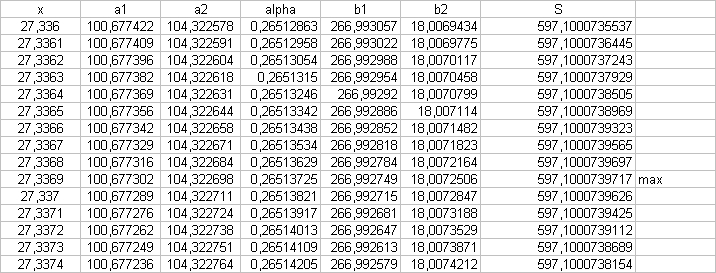
Pilage - marque de pageTout d'abord, merci et bravos aux trop peu nombreux qui ont répondu, tous correctement, à cette énigme. #13 - 08-04-2011 13:09:01
Pliage - marqu de page
Bêtement, je pensais que cela signifiait 3 chiffres apres la virgule The proof of the pudding is in the eating. #14 - 11-04-2011 11:47:09
Pliage - maque de pageBonjour, #15 - 12-04-2011 15:34:06
PPliage - marque de pageMerci Franky, c'est corrigé. Réponse rapideSujets similaires
Mots clés des moteurs de recherche |
 | ||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | ||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.