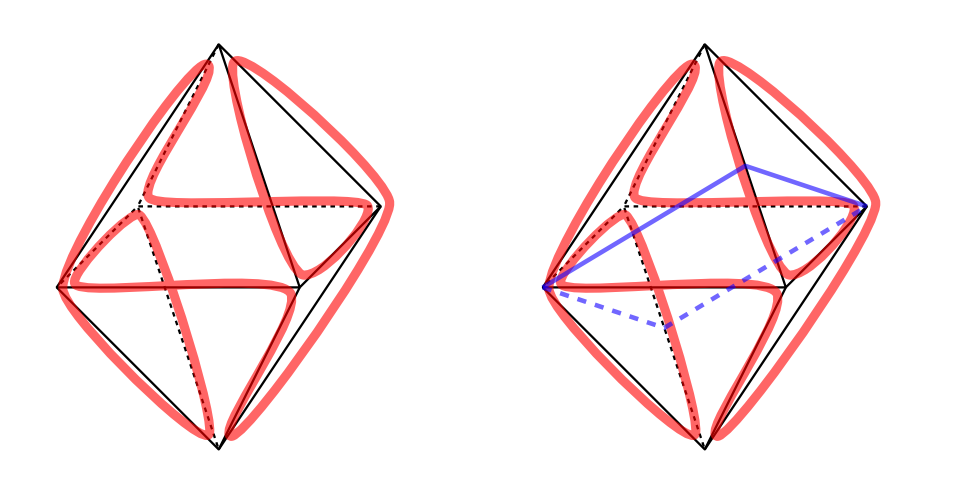
Soit un octaèdre régulier, on le considère comme un graphe. Chaque sommet est de degré 4, qui est pair : c'est donc un graphe eulérien. On sait donc depuis l'an de grâce 12³+2³ qu'il existe un cycle qui passe une et une seule fois par chacune des arêtes de ce graphe ; en réalité, il y en a même plusieurs.

Parmi tous ces cycles eulériens :

(1) trouver celui qui a le plus de symétries.
(2) trouver ceux qui en ont le moins.

Bon courage !

Exemple : sur la figure ci-dessous, on voit un cycle dessiné en rouge, de manière un peu approximative afin qu'on devine dans quel ordre les sommets sont parcourus.



Le groupe de ses symétries comporte 4 éléments :
* l'identité.
* la symétrie centrale dont le centre est le centre de l'octaèdre.
* la réflexion par rapport au plan dont l'intersection avec l'octaèdre est le losange bleu.
* la composée des 2 précédentes.