 |
#1 - 11-05-2020 11:46:57
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Longueur de cotnact
Bonjour à tous,
On colle l'un contre l'autre deux polygones superposables par translation sans qu'ils s'intersectent. S'il est facile de voir que la longueur de leur zone de contact peut approcher la moitié de leur périmètre, est-il possible de faire mieux?
Les polygones sont connexes (c'est à dire d'un seul tenant)
#2 - 11-05-2020 18:10:08
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
longueur de contaxt
Bonjour
Il est clair qu'on ne peut pas dépasser ni même atteindre la moitié . Dans le cas où la frontière commune est continue , c'est clair par déformation continue . Si la frontière est discontinue on augmente clairement le contact en la rendant continue .
J'avoue que ce n'est pas une démonstration d'une propreté nickel-chrome 
Vasimolo
#3 - 11-05-2020 19:36:11
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3586
- Lieu: 94110
Longueur dde contact
Est-ce vraiment volontaire de parler dans le titre de "Surface de contact", alors que la question qui suit parle de "longueur" ???
Tu ne précises pas non plus dans quel espace se situent tes polygones... Serait-ce dans un espace galiléen à deux dimensions ?
Spoiler : ? Si ce n'est pas le cas, je pense qu'il est facile de trouver un exemple pour lequel la longueur d'un coté commun peut tendre vers le périmètre. Je ne crois pas qu'il soit nécessaire de faire un dessin  . .
#4 - 11-05-2020 21:29:01
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Longueur de ccontact
Vasimolo
Il faudrait que tu m'éclaircisses ton propos, même si ce n'est qu'une intuition, car j'ai du mal à voir...
JackV
Je change si ça te gène.
Les polygones sont dans le plan euclidien.
#5 - 12-05-2020 08:47:25
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3837
Longueu de contact
Salut Caduk,
Désolé, je n'ai pas compris " Coller l'un contre l'autre.." et " superposable par translation".
#6 - 12-05-2020 10:09:36
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Longuuer de contact
nodgim
"Coller l'un contre l'autre.." signifie que les deux polygones partagent une partie de leur frontière, mais leurs intérieurs stricts ne s'intersectent pas. Par exemple, un pavage est un ensemble de figure géométrique collée les une aux autres sans intersection.
"superposable par translation" signifie que les deux polygones sont identiques et que l'on peut déplacer l'un des polygones par translation pour le poser sur l'autre de manière à ce qu'ils coïncident parfaitement. *il n'y a donc pas de rotation entre les deux polygones.
#7 - 13-05-2020 13:03:15
- TOUFAU
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 105
ongueur de contact
Bonjour Caduk,
On pourrait tendre vers 100% dans le cas d’une rotation (peigne avec rotation de 180°) ou d’un ‘polygone’ non connexe (juste les dents du peigne).
Mais je pense que la longueur de contact ne peut excéder 50% du périmètre dans le cas d’une translation de polygones connexes.
P est le polygone, L(P) la longueur de son périmètre, A et B ses deux instances dans le plan. A subit une translation par rapport à B. Ils ont une partie de leur périmètre en contact commun : cA et cB. L(cA))=L(cB). Ils ont aussi une partie de périmètre qui n’est pas en contact : nA et nB. L(nA) = L(nB) et L(cA)+L(nA)=L(P)
Remarque : le c de A et le c de B désigne les zones de contact respectives. Ça ne veut pas dire évidement qu’il s’agit de la même partie du périmètre de P instanciée sur A et B…
Tant que L(cA)<0,5L(P), la partie c de A peut correspondre à la partie n de B. Facile.
Dès que L(cA)>0,5L(P), L(cA)>L(nA) donc L(cA)>L(nB). Une partie de c sur A est aussi une partie de c sur B.
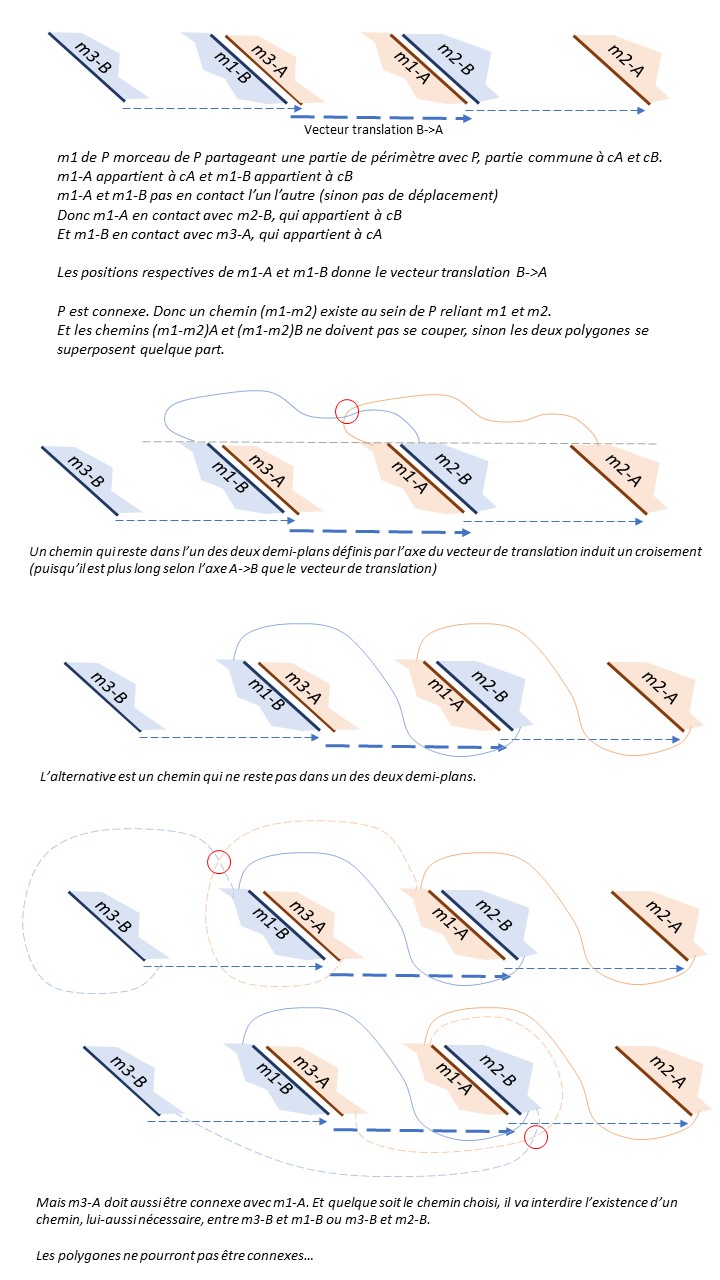
On peut donc trouver un ‘morceau de surface’ m de P, dont une partie du périmètre soit sur le périmètre de P, et dont l’instanciation sur A appartienne à cA ET l’instanciation sur B appartienne à cB. Et dans ce cas, on peut montrer que P ne peut être connexe.
Plutôt que de faire un long discours incompréhensible (sujet à nombreuses questions, cf précédent pb 😊), je tente un schéma.
#8 - 14-05-2020 00:37:24
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
longueir de contact
Toufau
Spoiler : [Afficher le message] J'ai le même schéma que toi, tu es sur la bonne piste 
Effectivement, intuitivement, on voit que quelle que soit la manière de relier les traits, il vont se croiser. Cependant il y a beaucoup de manières de relier les traits : ils peuvent tourner autour des morceaux, et ce plusieurs fois, les deux zones de contact peuvent avoir diverses orientations (ce qui fait que au lieu de tordre le trait, il peut être tout droit). Bref, il y a beaucoup de cas à analyser pour considérer ce résultat comme évident, il faudrait donc le prouver proprement (et c'est un peu le but de cette énigme).
Perso, ma démo est pas si évidente (mais relativement concise, j'évite les études de cas). Mais peut-être qu'il existe une preuve beaucoup plus élémentaire, je ne sais pas...
#9 - 14-05-2020 09:02:32
- TOUFAU
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 105
Longueur de ccontact
En fait pas tellement de variantes. Tout chemin restant dans un demi-plan par rapport à l'axe m1-B -> m1-A et plus long que le vecteur de translation A->B est interdit, sinon croisement (théorème des valeurs intermédiaires).
Pour le chemin (m1-m2)B, on croise nécessairement entre m1-B et m2-B pour éviter ça. Les deux parties de chemin situées chacune dans un des demi-plans sont alors plus courtes que le vecteur de translation. Mais on interdit de fait tout chemin qui croise entre les pièces entre m3-A et m2-A : il croiserait (m1-m2)B ou (m1-m2)A.
Le chemin (m3-m2)A doit donc être soit direct, soit passer par l'extérieur d'une des deux pièces m3-A ou m2-A. Dans les deux cas,une partie de ce chemin dans un des demi-plans sera plus long que le vecteur A->B. Il se croisera donc obligatoirement avec (m3-m2)B.
#10 - 14-05-2020 18:32:04
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
longieur de contact
Ce que je voulais dire ( car la propriété semble vraie au delà des polygones ) , c'est que pour une translation donnée , par exemple :
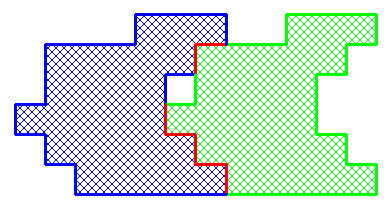
Si on étire la figure de gauche perpendiculairement à la direction de la translation et à périmètre constant ( disons avec des barres de Mécano ) alors on ne perd aucun contact avec la partie droite qui évolue de la même façon . Etirée au maximum , chaque partie est un triangle ou un quadrilatère et la réponse est immédiate .
Ce n'est pas très propre mais ça me semble correct .
Vasimolo
#11 - 15-05-2020 20:52:49
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
LLongueur de contact
Toufau
Spoiler : [Afficher le message] J'ai un peu de mal à suivre le raisonnement, je ne dit pas que c'est faux mais il faut que je regarde à tête reposée. Ton premier argument, même s'il me parait juste, me parait étrangement présenté. On peut très bien avoir le trait plus long que le vecteur A->B, sans que ça ne pose de problème pour le chemin (m1-m2)B (il faut tout de même passer entre les deux, ce qui me dit que ton argument est pas loin d'être juste. J'essaye de revenir plus tard pour comprendre mieux.
Vasimolo
Spoiler : [Afficher le message] Désolé, je ne comprend vraiment pas ce que tu entends par étirer à périmètre constant, et je ne vois pas comment en étirant ta figure, tu obtiens un rectangle u un triangle. Où se situe l'utilisation de la connexité dans ton raisonnement?
#12 - 16-05-2020 09:04:50
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3837
mongueur de contact
Il y a bien par exemple le colimaçon droit ( tous ses segments sont verticaux ou horizontaux) qui, en paire, forme un rectangle, donc pavable dans le plan. Mais je ne sais pas si ça rentre dans l'idée du superposable.
#13 - 16-05-2020 11:19:14
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Longuueur de contact
Non en fait mon idée ne marche pas à cause des rigidités aux points de contacts des deux polygones . Mais je me suis compliqué la vie pour rien 
Dans le polygone initial on retrouve deux fois la partie commune . En effet si on translate la partie commute par le vecteur opposé on reste dans la frontière du polygone et il n'y a pas d'intersection entre les deux parties .
Vasimolo
#14 - 16-05-2020 19:22:32
Longueur de contatc
Je sais pas si ma démonstration est assez rigoureuse mais moi je procede comme suis :
Soit deux polygones conexe P1 et P2 identiques par translation, on les place sur le plan de manière à ce qu'il soient collés.
On définit ainsi une ligne brisée L de contact entre les deux polygones.
On note V le vecteur de translation pour passer de P1 a P2
Le polynôme P2 possède deux fois cette ligne brisée. En effet : une fois au niveau du contact entre les deux polygones et une fois lorsque l'on transate cette ligne brisée avec le vecteur V.
Or c'est deux lignes ne se croisent pas car le polygone est conexe, donc le périmètre du polygone P2 est d'au moins 2 fois la longueur de la ligne brisée c'est à dire deux fois la longueur de contact.
Dites moi ce que vous en pensez
#15 - 16-05-2020 21:46:32
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Longueuur de contact
nodgim
Spoiler : [Afficher le message] Si par colimacon, tu entends une spirale, et que tu en imbrique deux l'une dans l'autre, alors oui, elle sont superposables, mais pas par translation (on est obligé de tourner la copie pour l'imbriquer dans l'autre, et on ne veut pas de rotation
Vasimolo
Spoiler : [Afficher le message] Je ne suis pas tout à fait sûr de comprendre ta nouvelle démo, mais si c'est bien ce que je comprend, ça ne marche pas. Demande toi si tu as utilisé la connexité, je ne la vois pas dans ta démo (Ou alors j'ai vraiment rien compris... 
Megatest
Spoiler : [Afficher le message] C'est la bonne idée de démonstration, mais il faudrait justifier pourquoi elles ne se croisent pas. Ce n'est pas si évident (en tout cas pas pour moi)
#16 - 17-05-2020 09:15:51
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3837
longuzur de contact
OK, tu avais d'ailleurs bien précisé dans l'énoncé: translation.
Donc, les 2 pièces jointes ont même orientation. Dans ce cas, je vois mal comment on peut dépasser 1/2. Si tel était le cas, aux pièces 1 et 2, on pourrait une pièce 3, même orientation, collée à la 2. Les longueurs communes 1-2 et 2-3 étant identiques, et indépendantes, 2 ne peut pas partager plus de la moitié de son périmètre avec 1 et plus de la moitié du périmètre restant avec 2.
#17 - 17-05-2020 15:29:36
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Longueur de conntact
nodgim
Spoiler : [Afficher le message]
Ok, tu as enfin compris l'énoncé 
Pourquoi les longueurs communes 1-2 et 2-3 sont indépendantes, ce n'est pas évident. Par exemple, c'est faux si on n'impose pas la connexité (je te laisse trouver un contre-exemple)
Je rajoute du temps
#18 - 20-05-2020 10:18:59
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
longieur de contact
J'ai la solution mais je n'ai pas le temps de rédiger avant ce soir , ce serait sympa de rajouter encore un petit peu de temps .
Merci d'avance 
Vasimolo
#19 - 20-05-2020 10:30:45
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Longueur e contact
Vasimolo
J'ai rajouté du temps 
#20 - 20-05-2020 17:08:34
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Longueur de conntact
J’aime beaucoup ces petits problèmes qui ne ressemblent à rien … J’ai d’abord essayé la formule de Pick , puis déformé les polygones , cherché à les orientés , et puis , et puis ….
Dans ces conditions , comme pour la pâte à crêpe , on laisse reposer ……………
On fait remonter une droite parallèlement à la direction de la translation jusqu’à atteindre les deux polygones ( on les atteint forcément en même temps ) . En continuant le mouvement , les parties gauches et droites des deux polygones vont suivre le même mouvement et on va les quitter en même temps .
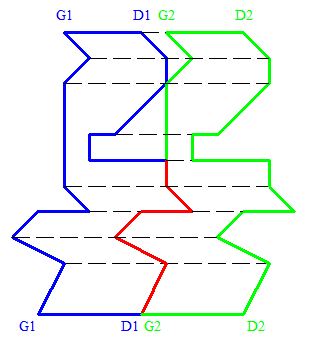
La longueur de la partie commune à D1 et G2 est inférieure ou égale à la somme des longueurs segments de D1 et G1 qui sont parallèles dans le mouvement de la droite ( en rouge sur le dessin ) donc clairement inférieure au demi-périmètre du polygone .
Vasimolo
PS : La figure ne cherche pas à rendre maximale la partie commune mais à illustrer les différents cas de figures .
#21 - 21-05-2020 09:49:57
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
longueur fe contact
Voilà une autre illustration peut-être un peu plus parlante :
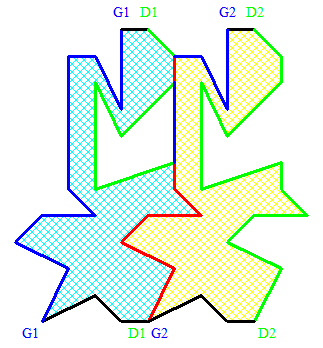
Le code couleur est le suivant :
Bleu = Gauche
Vert = Droite
Rouge = Commun
Noir = Rien du tout
La ligne G2 reste clairement à droite de la ligne D1 et on retrouve les segments rouges à la fois dans G1 et D1 .
Vasimolo
#22 - 21-05-2020 09:52:31
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Longueur de coontact
Vasimolo
Oui, impressionnant de simplicité comme démonstration, je n'en attendais pas moins de toi 
#23 - 21-05-2020 18:37:02
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3837
Longueur de contaact
J'avais fait un peu différemment: j'avais dessiné la ligne de contact ( continue ou pas, pas forcément polygonale, mais courbe libre) et reproduit cette ligne sur un calque. Par translation, j'avais déduit que les 2 lignes ne pouvaient pas se croiser sans couper en 2 la pièce.
#24 - 21-05-2020 18:59:41
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Longueur ed contact
Ce n'est pas bien clair mais ça revient à dire que D1 et G2 ne peuvent pas se croiser . A condition d'avoir défini proprement qui sont D1 et G2 .
Vasimolo
|
 |

 Accueil
Accueil
 Forum
Forum









