Un peu plus compliqué, celui-ci, j'avoue. Voilà donc la solution.
-- déjà, le roi blanc ne peut pas être en c2
-- Qui vient de jouer ?
-- Si c'est noir
---- Si le roi blanc n'est pas en b3
------ alors noir est en échec alors qu'il vient de jouer : c'est impossible
---- Donc : le roi blanc est en b3
---- Qu'a joué noir ? Il dispose d'une tour, d'un fou et d'un roi
------ Si c'est la tour : peu importe d'où elle vient, le fou faisait déjà échec au roi blanc : c'est impossible
------ Si c'est le fou : peu importe d'où il vient, la tour faisait déjà échec au roi blanc : c'est impossible
------ Si c'est le roi : idem, la tour et le fou faisaient échec : c'est impossible
---- Tous les cas sont impossibles
-- Donc : noir ne vient pas de jouer
-- Donc : blanc vient de jouer
-- Blanc ne dispose que d'un fou, et d'un roi
---- Si c'est le fou : il viendrait soit de b3, soit de c2. Dans les deux cas, noir aurait déjà été échec : c'est impossible
-- Donc : blanc vient de jouer le roi
-- D'où venait-il ?
---- S'il ne venait pas de b3, alors le roi noir aurait été échec : c'est impossible
-- Donc : blanc vient de jouer le roi, qui venait de b3
-- Blanc était à la fois en double échec ! Ca parait impossible, mais c'est la conséquence logique de nos déductions, et donc c'est forcément vrai.
-- Qu'a joué noir dans ce cas ?
---- La tour ? impossible, le fou fait échec
---- Le fou ? impossible, la tour fait échec
---- Le roi ? impossible, la tour et le fou font échec
Petite pause : ici, en général, les gens se disent : "Donc, c'est impossible". Mais non !
-- Donc : noir a joué une pièce qui a été capturée par le coup de blanc (le roi qui vient de b3)
-- Donc : blanc vient de jouer le roi, qui venait de b3, et a capturé la pièce jouée précédemment par noir
-- où est le roi maintenant ?
---- on peut éliminer a2, a4 b2, b4, c2, c4 (fou blanc, ou échec) : impossible
---- a3 ? quelle pièce aurait joué noir alors ? peu importe la pièce qu'on considère, elle ne résoudra pas le souci du double-échec : impossible
-- Donc : blanc vient de jouer le roi, b3c3, et a capturé la pièce jouée précédemment par noir
-- Quelle pièce permet de résoudre le souci du double échec ? Sans capture, aucune
-- Donc : blanc vient de jouer le roi, b3c3, et a capturé la pièce jouée précédemment par noir, qui a lui-même capturé une pièce blanche
-- Où était cette pièce blanche ?
---- En c3 ? dans ce cas la pièce pouvait être en b4, ou en c4, et bloquer "un" des deux échecs simultanés, mais pas les deux : impossible
Nouvelle petite pause : ici, en général, les gens s'accrochent se disent : "Donc, c'est impossible". Mais encore une fois, non !
-- Donc : blanc vient de jouer le roi, b3c3, et a capturé la pièce jouée précédemment par noir (en c3), qui a lui-même capturé une pièce blanche mais pas en c3.
-- Quel mouvement permet de capturer une pièce autrement que sur la case où on joue ? une seule solution : la prise en passant
-- Donc : blanc vient de jouer le roi, b3c3, et a capturé le pion noir joué précédemment, avec une prise en passant d'un pion blanc en c4 -- et qui venait nécessairement de c2 le tour d'avant.
-- d'où venait le pion noir ? de b4 ou de d4
---- d4 : la tour faisait déjà échec : c'est impossible
-- Donc : blanc a joué le roi, b3c3. noir avait joué un pion b4c3. blanc avait joué un pion c2c4.
-- Dans ce cas précis, pas de problème : blanc n'était pas échec, et se retrouve en double-échec juste ensuite.
-- Reste à vérifier que c'est possible : qu'a joué noir avant ?
---- Si le fou était déjà en d5, blanc aurait déjà été échec : c'est impossible
-- donc noir a joué son fou juste avant
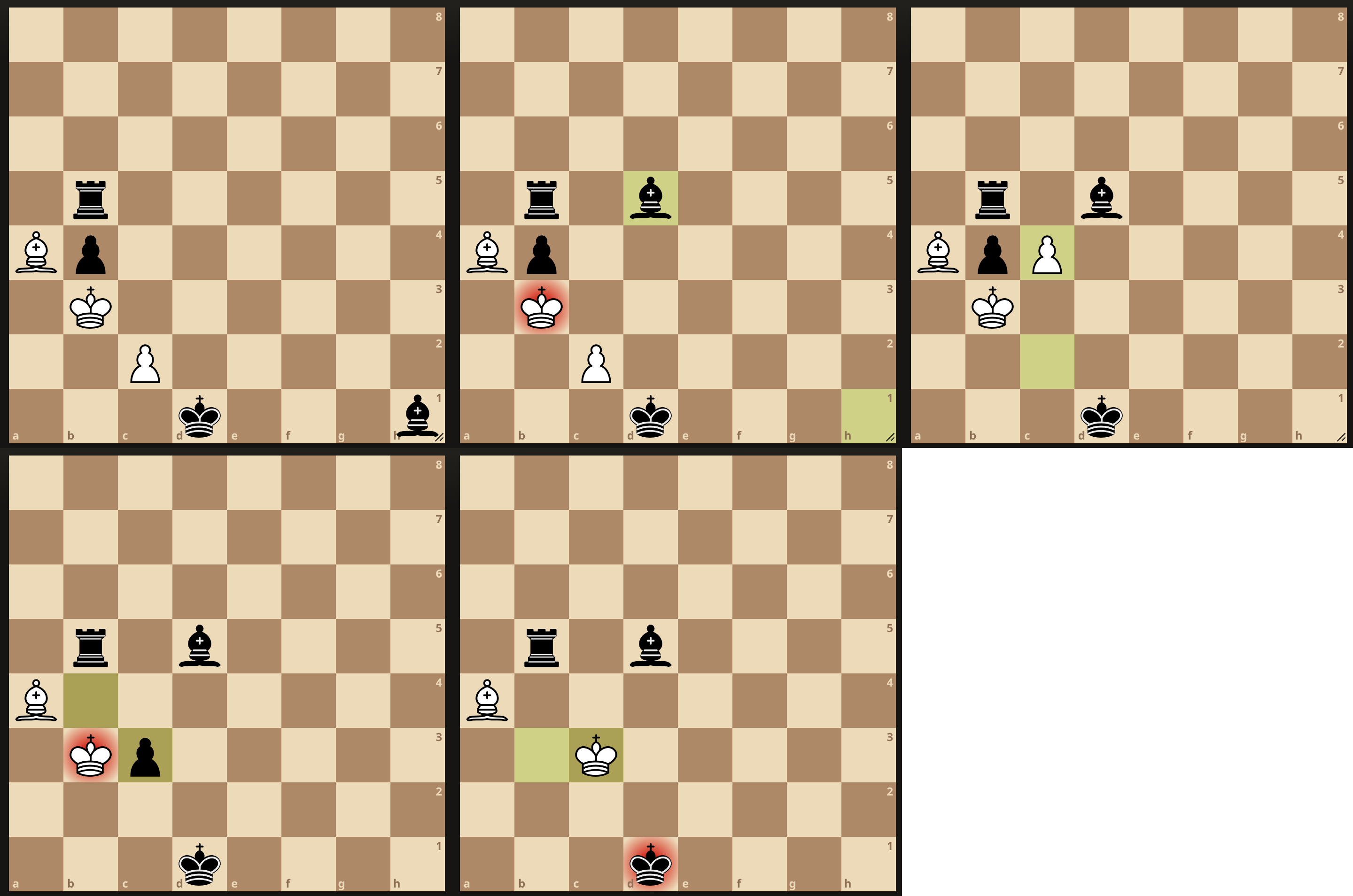
Conclusion finale : le roi blanc est en c3, il a capturé un pion noir, qui a lui-même pris un pion blanc en passant, qui a été joué suite à un coup du fou noir qui faisait échec.
Visuellement :

 Accueil
Accueil
 Forum
Forum








