Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 24-03-2024 23:33:10
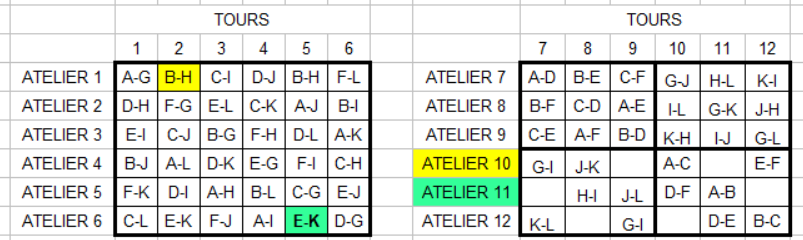
rotations pour olympuadesBonjour,
#0 Pub#2 - 25-03-2024 09:05:02#3 - 25-03-2024 19:48:47#4 - 26-03-2024 17:22:28
rotations pour olympiadeqPour moi les contraintes sont trop fortes . Il est possible que sur 11 créneaux les 12 équipes se rencontrent une fois et une seule mais si on impose en plus la présence de chacun à chaque atelier , ça devient ingérable . #5 - 30-03-2024 16:50:06
rotztions pour olympiadesC'est faisable, je l'ai déjà fait en colonie de vacances, mais avec 12 ateliers et chaque équipe n'en fait que 11. Réponse rapideSujets similaires
|
 | ||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | ||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.