EDIT condensé dans le dernier post

Alors je vais tenter de simplifier

Zig prend comme base des petits morceaux de même taille 1 unité arbitraire suffisamment petite (1/30 du bloc initial marche bien)

Au premier tour il en coupe 2.
Puce peut alors en éliminer 1 et le rattacher à l'ensemble, ou en attacher 2 et créer un morceau de taille 2.

Ensuite, à chaque découpe, tant qu'il n'y a que des morceaux de taille 1 ou 2 sur la table, Zig redécoupe 2 morceaux de taille 1 dans le bloc initial qui a un peu fonction de réserve infinie.
Si, par contre, Puce a créé un morceau de taille 3 , Zig le redécoupe en 3 morceaux.de taille 1 et si Puce a créé un morceau de taille 4, Zig le découpe en 1 1 et 2

A la fin d'une ènième découpe de Zig, avant l'assemblage de Puce, il n'y donc sur la table que le reste du bloc et n+1 morceaux de taille 1 ou 2.

A la fin de la seizième découpe (avant le 16e coup de Puce qu'il ne jouera pas), il y a 17 morceaux de taille 1 ou 2, et le reste du bloc.
Soit au moins 10 morceaux de même taille, auquel cas le jeu est fini.
Soit 8 morceaux de 1 et 9 de 2
Soit 9 morceaux de 1 et 8 de 2
Il s'agit de prouver que ces deux situations dans lesquelles Puce pourrait jouer son 16e coup auraient pu être évitées.

On part du principe que Zig a suivi fidèlement sa stratégie, donc dans chaque cas, il y a trois possibilités :
Zig vient de couper un morceau de 4 en 2 1 1
Zig vient de couper un morceau de 3 en 1 1 1
Zig vient de créer deux morceaux de 1

Premier Cas  8x1 et 9x2 :
Zig a coupé un morceau de 3 en 3x1, il aurait pu rajouter un morceau de 2 pris dans le reste.
Zig a Coupé un morceau de 4 en 2x1+2 , il aurait pu rajouter 2 morceaux de 2.
(ce cas est d'ailleurs impossible, car le morceau de 4 viendrait d'être créé à partir de 2 morceaux de 2 et donc, d'une situation perdante.)
Zig a rajouté 2x1 , il aurait pu rajouter un morceau de 2 à la place.

Second cas 9x1 et 8x2
Zig a coupé un morceau de 3 en 3x1, il aurait pu rajouter 2 morceaux de 2.
Zig a rajouté 2x1 , il aurait pu rajouter 2x2 à la place.

Zig a Coupé un morceau de 4 en 2x1+2 , et là, c'est plus délicat...
Il y avait donc 7x1, 7x2 et 1x4, un changement de la 16e découpe ne permet pas de conclure.
Il faut être un tout petit peu plus rétrograde et analyser la quinzième découpe...
Ce 4 a donc été assemblé juste avant par Puce, ce qui veut dire qu'à la fin de la 15e découpe, il y avait 7x1 et 9x2.

Cas 7x1 et 9x2 : (après la quinzième découpe, 16 morceaux et le reste)
Zig a coupé un morceau de 3 en 3x1, il aurait pu rajouter 1 morceau de 2.
Zig a rajouté 2x1 , il aurait pu rajouter 1 morceau de 2 à la place.
Zig a Coupé un morceau de 4 en 2x1+2 , il aurait pu rajouter 2x2 mais ce cas est de toute façon impossible puisque Puce aurait créé ce 4 à partir d'une situation perdante.

Tu sembles plus à l'aise que moi dans l'analyse directe et rétrograde , je m'y perds assez facilement .

1°) Si on considère que Zig joue son 16ème coup en utilisant ta stratégie principale , il y a bien 17 morceaux 1 ou 2 et un reste variable .
2°) Si on admet que Puce arrive à jouer son 16ème coup , il y aura possiblement sur la table au moins 15 morceaux 1 ou 2 et éventuellement 1 morceau 3 ou 4 et un reste .

Dans ton premier message tu remontais l'étude à partir du 16ème coup de Zig supposé non décisif et tu montrais qu'il pouvait modifier son coup précédent afin d'éviter cette déroute . L'analyse semble correcte mais il y a tellement de cas que je m'y perds

Dans ta deuxième proposition il me semble de tu démarres l'analyse rétrograde à partir d'un 16ème coup joué par Puce . Ensuite tu remontes pour voir comment Zig peut éviter cet échec .

Je ne mets pas en doute ton analyse d'autant que je suis parti sur le même modèle avant de chercher une autre partition du bloc initial .

Merci pour la participation

Vasimolo

Après relecture/réécriture , la réponse de Gwen est convaincante

Ce n'est pas si compliqué ( un peu quand même )

Vasimolo

@Jackv : La pâte à modeler ne quitte pas la table , on découpe , on repose , on colle et on repose

Vasimolo

Attention Migou , à chaque étape , Zig ne fait qu'extraire deux morceaux d'un même bloc

Vasimolo

Désolé , ta stratégie n'est pas claire . La première étape est facile : 3 blocs de 9 et Puce réagit : un bloc de 18 et un de 9 . Que fait Zig ???

Vasimolo

J'aurais bien laissé un peu plus de temps à Migou mais j'étais au maximum de la durée autorisée

Gwen a vite cerné le problème en remarquant qu'il fallait prélever des parts égales sur le bloc initial car alors chaque étape produra un nouveau morceau de 1 ou 2 . Après il faut accélérer la chose pour que 10 morceaux identiques apparaissent avant la fin de la 16ème étape et c'est plus compliqué . On peut comme Gwen imaginer des petits morceaux et négliger le reste et je vous laisse lire sa solution ou considérer que le bloc initial est composé de 27 parts ( ce qu'avait intuité Migou ) et la solution est plus rapide car le reste peut être utilisé comme une part .

Un grand merci aux participants

Vasimolo

Imaginons le bloc initial constitué de 27 pièces identiques . La stratégie de Zig dans un premier temps va consister à prélever deux pièces du plus petit bloc contenant au moins 3 pièces . Tant qu'il utilise ce procédé , chaque étape augmente de 1 le nombre de blocs et en dehors du bloc initial , il ne reste que des blocs de 1 ou 2 pièces éventuellement accompagnés d'un unique bloc de 3 ou 4 pièces . Zig peut utiliser cette stratégie tant qu'il dispose d'un bloc d'au moins 3 pièces c'est à dire dans le pire des cas jusqu'à la 15ème étape sauf s'il apparaissait huit blocs de 1 ou huit blocs de 2 pièces mais alors il pourrait conclure en récupérant les deux blocs manquant . Sinon à la 16ème étape , il trouvera huit blocs de 1 pièce ou l'une des configurations suivantes qui lui permettra aisément de gagner :



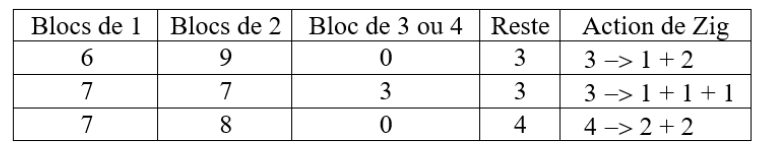
Vasimolo

Un peu tout de même car avec 28 morceaux Zig pourrait se retrouver coincé avec six morceaux de 1 , huit morceaux de 2 et deux morceaux de 3. Les 27 parts étaient choisies pour régler le 7-7 blocs de 1-2 sans remonter à l'étape antérieure . On peut bien sûr faire d'autres choix

Vasimolo