Comme je suis assez mauvais en maths , je suis allé sur ce site http://www.terre-net.fr/applets/cuve/cuve.asp et j'ai obtenu une longueur de cuve de 350,15 cm, un reste de 9434 litres pour une hauteur de 1,60m, auquel je soustrais les 34 litres utilisés en attendant le livreur, ce qui nous amène à 11000 - 9400 soit 1600 litres à la commande, et merci Google

- la cuve est un cylindre dont la base est un cercle de deux mètres de diamètre ; son volume est de 11 mètres cube. Donc la hauteur de la cuve est telle que
[TeX]\pi R^2 \times h = 11[/TeX]
Soit [latex]h = \frac {11}{\pi}[/latex] mètres (on arrondira plus tard, mais ça fait dans les trois et demie).


- cette cuve est remplie jusqu'à une hauteur d'un mètre soixante ; le volume de fioul restant est donc :
[TeX]V_{fioul} = S \times h = S \times \frac {11}{\pi}[/latex] où S est la surface d'un cercle de deux mètres de diamètre coupé par une corde dont la distance maximale au cercle lui-même est de 40 centimètres (la "différence de niveau", à ceci près qu'ici on ne considère pas que cette corde est "horizontale" sur un cercle "vertical", vu que ce n'est qu'une question de repère, mais tout ça n'est que de l'enc**age de mouches mathématco-mathématicien, plouf plouf).

Comment calculer ça ?..



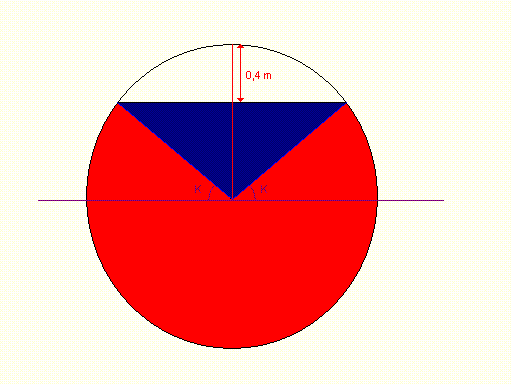
Valeur de l'angle K : [latex]K = arcsin(0,6)[/latex] (bah oui, on est dans un cercle de rayon 1, alors faisons un peu de trigonométrie )

Valeur de l'aire rouge : [latex]S_1 = \frac {\pi + 2 K} {2 \pi} \times \pi R^2 = \frac {\pi + 2 arcsin(0,6)} {2}[/TeX]
Pour ce qui et de l'aire bleue, on remarque qu'en réunissant les deux triangles délimités par le rayon rouge, on obtient un carré dont les deux côtés sont respectivement le sinus et le cosinus de K ; l'un des deux vaut 0,6, l'autre vaut donc [latex]\sqrt{1 - (0,6)^2} = 0,8[/latex] d'où : [latex]S_2 = 0,6 \times 0,8 = 0,48[/latex]



Volume de fioul restant dans la cuve :
[TeX]V = (S_1 + S_2) \times \frac {11}{\pi}[/TeX]
Volume à rajouter pour la remplir (en mètres cubes) :
[TeX]V_r = 11 - (\frac {\pi + 2 arcsin(0,6)} {2} + 0,48) \times \frac {11}{\pi}[/TeX]
On obtient 1,56616339 mètre cube (merci la calculette Google : la caltos Windows ne connait pas l'arc-sinus).

Soit 1566 litres à rajouter.

Mais il faudra les rajouter dans deux jours, et dans deux jours 34L de fuel en plus auront été consommés. C'est donc 1600 litres qu'il faut commander.

CQFT (ce qu'il fallait trouver )

J'avais déjà eu ce problème à résoudre dans la vraie du temps où je me chauffais au fuel mais je n'ai pas eu le courage de m'y remettre en cette période de Noël. Et puis moi mes cours de math c'est vraiment de l'histoire ancienne.