A ce stade, je voudrais expliquer comment on calcule la diamètre des sphères dans les cas de figures donnés ci-dessus.
Prenons l'exemple de 2 sphères:
Il y a 2 pratiquement methodes:
1) on place les sphères dans un cube virtuel, et on pose l'equation de la diagonale:
[TeX]sqrt{3}[/latex] = [latex]sqrt{3}[/latex]R + R + R + [latex]sqrt{3}[/latex]R
on en déduit que R= [latex]\frac {sqrt{3}} {2+2sqrt{3}}[/latex] ou encore que D = [latex]\frac {sqrt{3}} {1+sqrt{3}}[/TeX]
2) on place des points (qui representent plus tard les centre de sphères, dans un cube de 1x1x1, de manières à ce que ces points soient le plus éloignés les uns des autres. Pour 2, c'est simple, il sont placés sur 2 coins opposés:
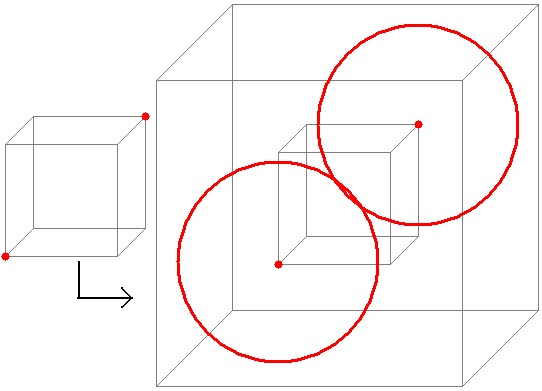
la distance qui les sépare est tout simplement [latex]sqrt{3}[/latex] . Maintenant il nous faut convertir cette dimension dans le probème qui nous interesse. Pour ca, il suffit de diviser par la dimension du cube qui contiendrais les sphères si les centres sont inscrits dans un cube de 1x1x1. Si X est la distance entre les centre 2 centres, et donc egalement le diametre des sphères, pour trouver la dimension de ce grand cube, on rajoute tout simplement le rayon de chaque coté: GrandCube= X/2+1 + X/2, soit 1+X. Maintenant puisque le problème est donné avec un cube initial de taille constante = 1:
Soit X la distance entre 2 centres dans le problème simplifié, le diamètre des sphères D = [latex]\frac {X} {1+X}[/latex]
Donc, pour 2 sphères on trouve [latex]\frac {sqrt{3}} {1+sqrt{3}}[/latex]
Si la 1ère méthode parait simple pour 2 sphères, ca se complique rapidement pour un plus grand nombre de sphères.
De la même manière:
pour 3 et 4 sphères:
X = [latex]{sqrt{2}[/latex], donc D = [latex]\frac {sqrt{2}} {1+sqrt{2}}[/latex]
Et oui, le meilleur arangement pour 3 et 4 sphères est le même. Pour 3 sphères, il suffit d'en enlever une.
pour 5 sphères:
X = [latex]{sqrt{\frac {5}{4}}[/latex], donc D = [latex]\frac {sqrt{5}} {2+sqrt{5}}[/latex]
pour 6 sphères:
on pose: X=[latex]sqrt{{a^2}+1+{a^2}}[/latex] et X=[latex]sqrt{(1-a)^2+(1-a)^2}[/latex] on en deduit que:
1=4a puis b=[latex]\frac {3}{4}[/latex] puis X = [latex]\frac{3sqrt{2}}{4}[/latex] puis D = [latex]\frac {3sqrt{2}} {4+3sqrt{2}}[/latex] ou [latex]9-6sqrt{2}[/latex]
(encore bravo à Vasimolo au passage)
pour 7 sphères:
Voici d'abord à quoi ressemble l'arangement optimal des 7 sphères:

Dans cette configuration, une seule sphère est dans un coin. On calcule d'abord la distance qui sépare un bord à une des sphères qui touche celle du coin, puis aprés quelques pages de calculs que je vous épargnerais, on trouve:
X=[latex]sqrt{\frac{16+2sqrt{3}-8sqrt{\frac{5}{2}+sqrt{3}}}{3}}[/latex]
puis:
D=[latex]\frac{sqrt{\frac{16+2sqrt{3}-8sqrt{\frac{5}{2}+sqrt{3}}}{3}}}{sqrt{\frac{16+2sqrt{3}-8sqrt{\frac{5}{2}+sqrt{3}}}{3}}+1}[/latex] soit 0.458897882
Pour 8 et 27 sphères:
Il est évident que les solutions sont 1/2 et 1/3, avec une configuration cubique, cependant ca s'arrète là. Pour 64 sphères, il existe un arangement qui est plus optimal que la configuration cubique.
Pour 9 sphères:
configuration donnée par lefredj: une sphère dans chaque coin, et une au centre du cube:
X = [latex]{\frac {sqrt{3}}{2}[/latex], donc D = [latex]2sqrt{3}-3[/latex]
Pour 10 sphères: (voir configuration page précédente)
On trouve X = [latex]\frac {3}{4}[/latex] donc D = [latex]\frac {3}{7}[/latex]
Pour 11 et 12 sphères:
Les configurations sont connues, mais les calculs sont si compliqués que l'on ne connait qu'une approximation trouvé par ordinateur.

 Accueil
Accueil
 Forum
Forum







