Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 06-09-2010 18:28:07
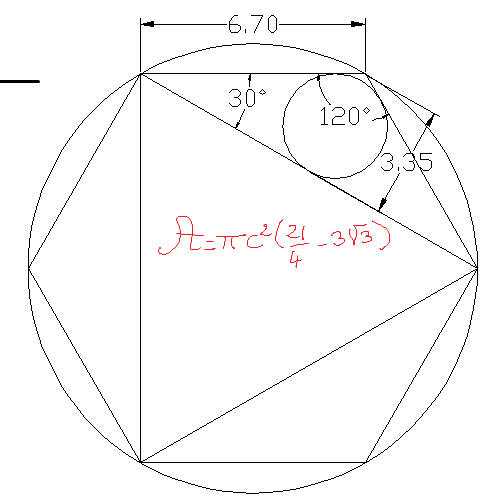
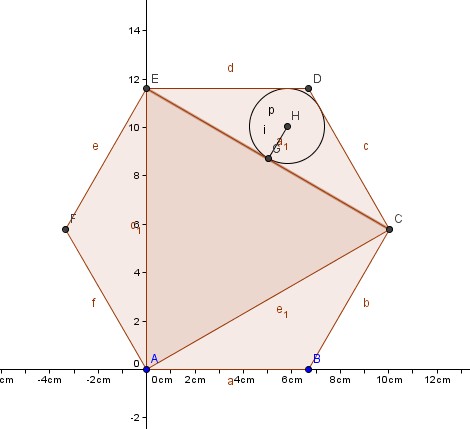
Enigmaform1aOn construit un hexagone régulier de 6,7 cm de coté. Puis à l'aide de trois côtés, on forme un triangle equilatéral.on obtient donc un hexagone, avec un triangle equilatéral au centre, et 3 petits triangles sur les côtés. Un promath- actif dans un forum actif
#0 Pub#2 - 06-09-2010 18:56:15#3 - 06-09-2010 19:21:58#4 - 06-09-2010 23:06:14
enugmaforma1Soit c la longueur des 6 cotes de l'hexagone. The proof of the pudding is in the eating. #5 - 06-09-2010 23:27:42#6 - 07-09-2010 08:24:22
znigmaforma1Bonjour, #7 - 07-09-2010 16:58:09
Enigmaformma1Bonjour j'avais mis une mauvaise réponse car j'avais calculé le rayon 1 centième inférieur à vous. Ce qui a franchement bouleversé tous mes calculs par la suite. Réessayez votre réponse, et pardonnez moi infiniment! Un promath- actif dans un forum actif #8 - 07-09-2010 17:18:05#9 - 07-09-2010 17:20:04#10 - 08-09-2010 02:00:47
enigmafoema1la taille maximale des cercles dans les petits triangles: R=segment * (sqrt(3)-3/2) = 0.23205080756887729352744634150587 * 6.7 = 1.5547404107114778666338904880893 Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt #11 - 08-09-2010 12:11:52
Enigmaformaa1graphiquement Dans le cadre de la quinzaine du beau langage, ne disez pas disez, disez dites. (Julos Beaucarne) Réponse rapideSujets similaires
Mots clés des moteurs de recherche
|
 | ||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | ||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.