J'ai récemment acheté une machine. Sur cette dernière, il y a un cylindre en rotation sur lequel est fixée une bande abrasive comme le montre l'animation (la bande est en rouge).
Plein Ecran / Télécharger SWF
J'achète donc des rouleaux de bande d'une certaine largeur que je dois découper judicieusement pour pouvoir faire le montage...
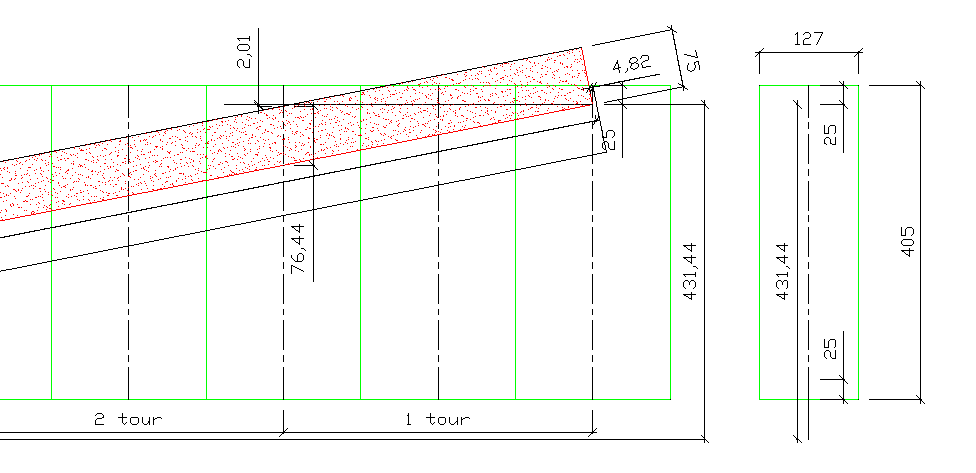
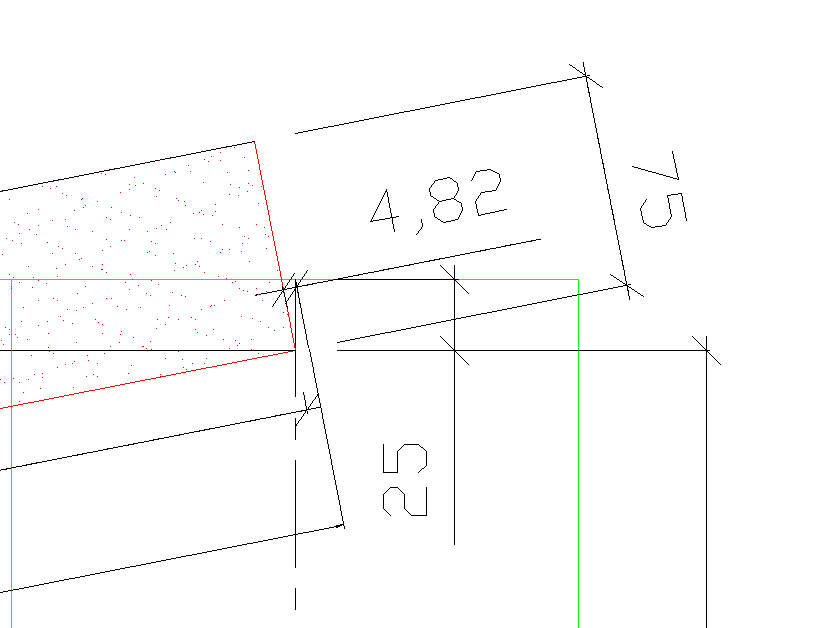
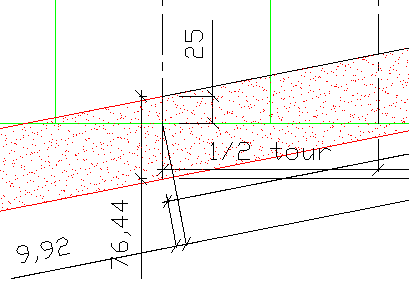
Les extrémités de la bande passent à l'intérieur de petites fentes se trouvant à chaque extrémité du cylindre et sont pincées par un mécanisme à l'intérieur. Les arrêtes des fentes en contact avec la bande (sur lesquelles cette dernière est pliée) sont dans un même plan passant par l'axe du cylindre.
Il ne faut pas que les enroulements de la bande soient jointifs mais qu'il y ait un jour de l'ordre de quelques millimètres.
On trouve dans le commerce des rouleaux de largeur [latex]B_1=75 mm[/latex] et [latex]B_2=100 mm[/latex].
Les données sont les suivantes:
Diamètre du cylindre: [latex]D=127 mm[/latex]
Longueur du cylindre: [latex]L=405 mm[/latex]
longueur des fentes: [latex]l=25 mm[/latex]
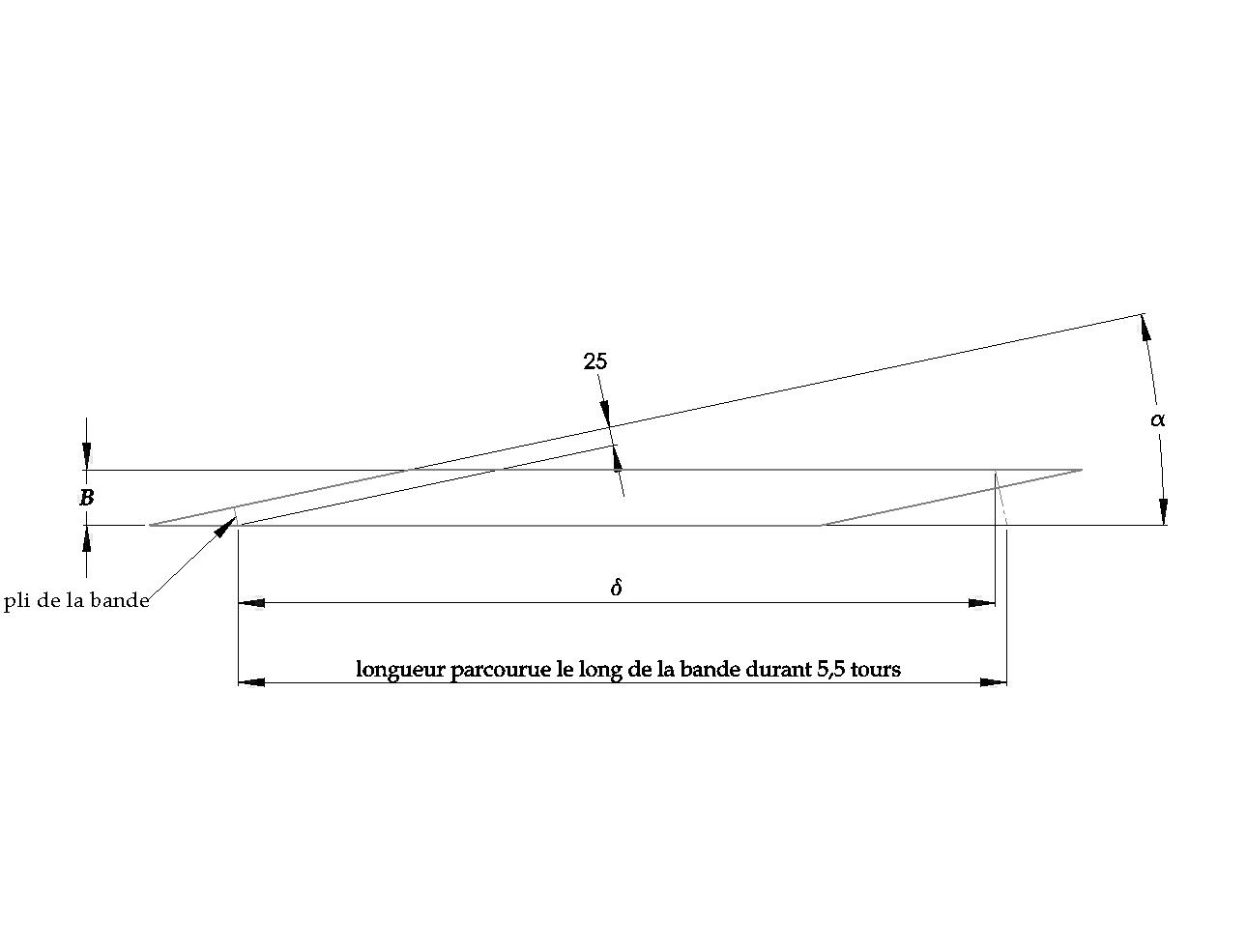
Voici à quoi ressemble la bande découpée et déroulée (possibilité de faire un zoom).

Quel rouleau me donnera le meilleur montage et quelles sont les valeurs de [latex]\alpha[/latex] et [latex]\delta[/latex] qu'il faut que je prenne, pour faire le bon découpage?
Bon courage et bonne prise de tête!

 Accueil
Accueil
 Forum
Forum