 |
#1 - 05-12-2010 12:28:06
- EfCeBa
- Administrateur
- Enigmes résolues : ∞+1
- Messages : 3×2087
5 nombres entiers autour du'n cercle
On écrit 5 nombres entiers naturels autour d'un cercle, de telle sorte que la somme de deux ou trois nombres adjacents ne soit jamais divisible par 3.
Parmi ces cinq nombres, combien sont des multiples de 3 ?
PS : Je suis désolé d'avoir à avouer celà mais j'ai piqué cette énigme sur un devoir maison, et thim57 semblait tellement triste de ne pas trouver que je me suis dit qu'on pouvait l'aider... (ici)
#2 - 05-12-2010 12:42:50
- Klimrod
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 4054
- Lieu: hébesphénorotonde triangulaire
5 nombres entiers autour d'un cerlce
Seule réponse possible : 2
Exemple : 3-1-3-1-1 (ou 3-2-3-2-2)
Démonstration par l'absurde :
- s'il y a 3 multiples de 3 (ou plus) : alors on peut trouver deux multiples de 3 qui sont adjacents. Et leur somme est un multiple de 3, ce qui est interdit.
- s'il y a 0 ou 1 seul multiple de 3, alors on peut trouver trois nombres adjacents qui ne sont pas multiples de 3.
Appelons-les i, j et k.
Puisque i n'est pas un multiple de 3, alors i est congru à 1 ou à 2 modulo 3. Puisque i+j n'est pas un multiple de 3, cela implique que j ait la même congruence que i modulo 3. Même raisonnement pour j et k, impliquant que j et k aient la même congruence modulo 3. Et si on additionne i+j+k, alors on trouve que i+j+k est congru à 0 modulo 3, ce qui est interdit par l'énoncé.
- donc il ne peut y avoir que 2 multiples de 3, ce qui est prouvé par les deux exemples fournis au début.
Klim.
J'ai tant besoin de temps pour buller qu'il n'en reste plus assez pour bosser. Qui vit sans folie n'est pas si sage qu'il croit.
#3 - 05-12-2010 12:44:44
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,192E+3
5 nombres entiers autour d'u ncercle
Aucun, un exemple suffit : 2 2 4 2 1 => sommes = 8 8 7 5 5
Maintenant, il faut peut-être regarder s'il ne peut pas y en avoir 1 2 3 4 ou 5
Pour 4 et 5 c'est réglé puisque 3 multiples de 3 seraient consécutifs. donc impossible
Si il y en a 1 : appelons le "x"
abcdx :
c+d est non multiple de 3
a+b est non multiple de 3
a+d est non multiple de 3
maintenant , modulo 3 : il ne faut pas que la somme de 3 des ces nombres modulo3 soit multiple de 3
x mod3= 0
si a mod 3 = 1 alors, b mod3=1 , donc c mod3=2
Mais si a mod = 1 , et x mod 3= 0 on a aussi d mod3=1 donc cmod 3 =1
si a mod 3 = 2 alors, b mod3=2 , donc c mod3=1
Mais si a mod = 2 , et x mod 3= 0 on a aussi d mod3=2 donc cmod 3 =2
Un seul multiple de 3 aboutit donc à un cas impossible
S'il y en a 2 : appelons les x et y
abcxy : a b et c ne peuvent pas avoir tous le même modulo car leur somme serait divisible par 3, conséquence: a+b ou b+c sera multiple de 3
donc y+a+b ou b+c+x le sera aussi Cas impossible
abxcy : 22323 ça marche, donc il peut y en avoir 2 dans cette configuration et ses variantes. On voit facilement que a b et c doivent être de même modulo3 non nul mais ça marche
Dernier cas : 3 multiples de 3 x y et z
ils sont non consécutifs bien sûr :
axybz : même raisonnement que le cas précedent 13313, ça marche a et b doivent juste être de même modulo 3 non nul
Donc, il peut y avoir 0, 2 ou 3 multiples de 3 autour de ce cercle.
#4 - 05-12-2010 14:52:00
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
5 nombres entiers autur d'un cercle
Je dirais deux. En appelant A, B, C, D, E ces nombres, je pense que :
- A et D multiples de 3
- B, C et E ayant la même congruence modulo 3
est la seule solution (aux rotations près) donnant le résultat attendu.
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#5 - 05-12-2010 15:07:26
- scrablor
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 965
5 nombres entier autour d'un cercle
C'est amusant.
On peut remplacer un nombre par son reste dans la division par 3 qui sera 0, 1 ou 2.
Un 0 n'a jamais un 0 pour voisin, ni deux voisins 1 et 2.
Un 1 n'a jamais un 2 pour voisin, ni deux 1 pour voisins.
Un 2 n'a jamais un 1 pour voisin, ni deux 2 pour voisins.
Il ne reste que deux configurations à une rotation près :
Il y a donc deux multiples de 3.
Celui qui fuit les casse-tête ne vaut pas un clou.
#6 - 05-12-2010 15:16:40
- franck9525
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1935
- Lieu: 86310
5 nombres entiers autour dun cercle
3,1,1,3,1 donnent 2 des entiers sont divisibles par trois.
The proof of the pudding is in the eating.
#7 - 05-12-2010 17:52:02
- Tromaril
- Habitué de Prise2Tete
- Enigmes résolues : 20
- Messages : 45
5 nombres entiers autoue d'un cercle
On peut raisonner modulo 3, il n'y alors sur le cercle que des 0, des 1 et/ou des 2.
Deux 0 ne peuvent pas être côte à côte, il y a donc au maximum deux 0 sur le cercle.
Un 1 ne peut pas être mis à côté d'un 2, donc si il y a un 1 sur le cercle, il est entouré soit de deux 0, soit d'un 1 et d'un 0 (raisonnement symétrique s'il y a un 2).
Enfin la succession 1--0--2 est interdite.
Cela ne laisse que deux possibilités
-1--0--1--0--1- ou -2--0--2--0--2-
Il y a donc deux nombres divisibles par 3
#8 - 06-12-2010 11:47:22
- Yannek
- Passionné de Prise2Tete
- Enigmes résolues : 10
- Messages : 60
5 nombres entoers autour d'un cercle
Deux des cinq nombres sont multiples de 3.
S'il y en avait davantage, deux seraient consécutifs.
S'il n'y en avait qu'un, il serait entouré par deux nombres égaux modulo 3. (101) ou (202). Par unicité du zéro et par la règle des deux nombres consécutifs non divisibles par 3, on a (22022) ou (11011) dont trois nombres consécutifs sont égaux modulo 3: impossible.
S'il n'y avait aucun 0, un série de trois nombres consécutifs en contient (modulo 3) un couple 12 ou 21 (impossible) ou est composée uniquement de 1 ou de 2 (impossible).
#9 - 06-12-2010 13:10:17
- Milou_le_viking
- Professionnel de Prise2Tete
- Enigmes résolues : 30
- Messages : 446
5 nomvres entiers autour d'un cercle
J'ai la séquence
1 - 1 - 3 - 1 - 3
La somme de deux nombres adjacents donne 2 ou 4.
La somme de trois nombres adjacents donne 5 ou 7.
Il y a forcément 2 nombres multiples de 3.
Ceci vient du fait que les chiffres peuvent être classés comme ceci:
Les 3n-1, les 3n et les 3n+1.
Il en découle trois règles:
- Un 3n-1 et un 3n+1 ne peuvent pas être adjacents ni de part et d'autre d'un multiple de 3 puisque leur somme est multiple de 3.
- Il ne peut pas y avoir plus de 2 nombres adjacents du même type puisque leur somme serait multiple de 3.
- Deux multiples de 3 ne peuvent pas être adjacents puisque leur somme est également multiple de 3.
Il faut donc obligatoirement un multiple de 3 puis un ou deux non multiples de 3 de même type (soit deux 3n-1 soit deux 3n+1) puis un nouveau multiple de 3, etc.
La séquence est donc composée de 3n et soit toujours des 3n+1 soit toujours des 3n-1, seul ou par paire, qui séparent les multiples de 3.
Autre solution avec que des 1 :
1 - 111 - 1111 - 111111 - 1111111
On peut ainsi toujours garnir un cercle d'une quantité arbitraire de nombres. Ca marche pour 5, mais pour plus aussi et moins bien sûr.
#10 - 06-12-2010 14:48:38
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1823
5 nombres entiers autour dun cercle
Bonjour !
Tout nombre entier peut s'écrire sous la forme
3k (forme "0")
ou 3k+1 (forme "1")
ou 3k+2 (forme "2")
(k entier naturel)
On cherche donc à placer sur un cercle 5 nombres de ces formes.
Or selon l'énoncé, la première contrainte d’indivisibilité par 3 de la somme de deux nombres adjacents se traduit par :
- deux nombres de la forme "0" ne peuvent être adjacents car leur somme est divisible par 3
- un nombre de la forme "1" ne peut pas être adjacent à un nombre de la forme "2" non plus pour les même raisons
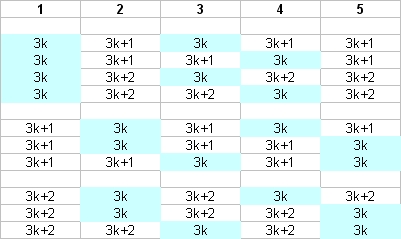
La deuxième contrainte (sommes de trois termes adjacents indivisible par 3) limite encore plus les possibilités, listées dans le tableau ci-dessous :
sur les 10 lignes du tableau, certaines sont identiques par permutation circulaire, je les laisse quand même ...
On voit surtout que chacune des possibilités demande 2 nombres multiples de 3
Merci, à bientôt,
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#11 - 06-12-2010 16:04:46
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
5 nombres entiers autour d'un cerclee
Assez atypique...
Je raisonne modulo 3. Je ne considère donc que 0, 1 et 2.
La question devient: combien y a-t-il de 0?
Il est évident que 3 nombres identiques ne peuvent se suivre, que deux 0 ne peuvent se suivre, que 1 et 2 ne peuvent se suivre, que 0 1 2 ne peuvent se suivre d'après l'hypothèse.
Tout d'abord, il faut noter qu'il y a au moins un 0. En effet sinon il n'y a que des 2 et des 1. Comme il ne peut pas y avoir de 1 à côté d'un 2 (1+2=3), il n'y a que des 1 ou que des 2 mais alors la somme de 3 nombres adjacents est divisible par 3. Il y a donc forcément au moins un 0. Comme hormis ce 0, il reste 4 cases adjacentes, le même raisonnement nous dit qu'il en faut même au moins un second (sinon quatre 1 ou quatre 2 se suivent). Il y a donc au moins deux 0. Or comme deux 0 ne peuvent se suivre, il ne peut pas y en avoir trois ou plus sinon deux d'entre eux seraient adjacents. Donc si une telle configuration existe, elle a exactement deux 0 donc deux nombres multiples de 3.
Vérifions si une telle solution existe (et voire même quelles sont-elles).
Que peut-on mettre à côté d'un 0? Pas un 0. On peut mettre un 1 mais alors dans ce cas, de l'autre coté du 0, on ne peut mettre ni 0 (0+0=0 divisible par 3) ni un 2 (0+1+2=3), donc la combinaison est: 1 0 1. Si on met un 2, on doit en mettre un de l'autre côté aussi pour la même raison et la combinaison est 2 0 2.
Comme il y a deux 0, il y a deux fois: 1 0 1 ou 2 0 2 (il ne peut pas y avoir 1 0 1 et 2 0 2 sur la même solution car cela fait 6 nombres).
Il n'y a donc que deux solutions modulo 3:
1 0 1 0 1 aux rotations près
2 0 2 0 2 aux rotations près.
En voici 2 exemples concrets:
4 3 7 6 10
5 9 8 6 2
Merci pour cette énigmette.
#12 - 06-12-2010 23:31:45
- dylasse
- Professionnel de Prise2Tete
- Enigmes résolues : 21
- Messages : 381
5 nombre entiers autour d'un cercle
2.
Chaque nombre peut être remplacé par son reste modulo 3. Il faut donc placer des 0, des 1 et des 2 sur un cercle.
On démontre alors que, si il y a un 1, à coté de lui, il n'y a pas de 2, et il n'y a pas plus d'un 1 (chaque 1 à donc au moins 1 voisin 0). Deux 0 ne peuvent se toucher et chaque 0 est entouré du même nombre. Donc il y a une séquence 1 0 1. Ce qui donne 1 0 1 1 0 ou 1 0 1 0 1, ce qui revient au meme.
Même solution si il y a un 2 : 2 0 2 2 0.
C'est le genre de problème qui est plus dur à expliquer qu'à comprendre...
#13 - 07-12-2010 11:19:29
- naddj
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 301
- Lieu: Ffm
5 nombrres entiers autour d'un cercle
Ma réponse ne respire clairement pas la rigueur mathématique, mais comme je ne me souviens plus comment je devrais démontrer/rédiger cela...
Soient a,b,c,d,e entiers naturels.
Pour mettre en évidence la divisibilité par 3 de ces entiers naturels, on considère que pour chacun de ces nombres, il existe un k, entier naturel, tel que ces nombres soient égaux à 3k, à 3k+1 ou à 3k+2.
Les nombres étant placés sur un cercle, je prends a=3k.
En appliquant la consigne de somme 2 à 2 et 3 à 3 non divisibles par 3, on trouve les 4 séries suivantes :
a=3k, b=3k+1, c=3k, d=3k+1, e=3k+1
a=3k, b=3k+1, c=3k+1, d=3k, e=3k+1
a=3k, b=3k+2, c=3k, d=3k+2, e=3k+2
a=3k, b=3k+2, c=3k+2, d=3k, e=3k+2
Dans tous les cas, on a donc 2 des 5 entiers naturels qui sont multiples de 3.
Réciproquement, on avait nécessairement au moins un des entiers égal à 3k, car :
Supposons qu'aucun des entiers ne soit multiple de 3.
Hyp 1: a=3k+1 => b=3k+1 (car si b=3k+2, alors a+b est multiple de 3)
=> c pas de solution. (si c=3k+1, alors a+b+c multiple de 3, et si c=3k+2, alors b+c multiple de 3).
Hyp 2: a=3k+2 => b=3k+2 (car si b=3k+1, alors a+b est multiple de 3)
=> c pas de solution. (si c=3k+2, alors a+b+c multiple de 3, et si c=3k+1, alors b+c multiple de 3).
Tout ca pour dire que la réponse est 2.
#14 - 07-12-2010 18:54:41
- blaxe
- Habitué de Prise2Tete
- Enigmes résolues : 27
- Messages : 12
5 nombres entiers autour d'un crcle
Déjà, puisque on parle de la divisibilité par trois, on peut mettre tous les nombres modulo 3.
Déjà, trois nombres côtes à côtes, puisque leur somme n'est pas divisible par 3, on ne peut avoir 3 chiffres differents (1+2+0=3, or 3l3 (le signe "l" signifie divise))
Donc deux de ces chiffres sont égaux. De plus, on ne peut accoler un 1 et un 2 puisque dans ce cas on a 1+2=3 et 3l3 !
On ne peut pas non plus aligner trois nombres égaux puisque k+K+K=3K et 3l3K !
Enfin, on ne peut accoler deux 0, puisque 0+0=0 et 3l0
On peut donc juste avoir 101, 202, 220 ou 110 pour trois chiffres accolés !
Les seules solutions sont 20202 et 10101, ce qui fait donc deux nombres divisibles par 3 !
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum







