Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 09-03-2011 15:41:35#0 Pub#2 - 09-03-2011 16:53:27
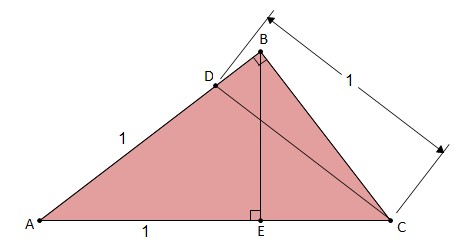
tri_1_gmeOn va donner du Pythagore ! #3 - 09-03-2011 17:46:53
tri_1_gmeJe trouve [latex]\sqrt[3]2-1\approx 0.2599210498948731647672106072782[/latex] #4 - 09-03-2011 18:03:43
tri_1_hleQuatre triangles rectangles pour quatre inconnues, on devrait s'en sortir, non ? Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298 #5 - 09-03-2011 20:57:51#6 - 10-03-2011 08:25:00
Tri1_gleBonjour, #7 - 10-03-2011 12:56:56
tri_1_fleBD vaut un certain X qui repond a l'equation: Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt #8 - 10-03-2011 15:55:18
tri_1_gmesoit [latex]\alpha[/latex] l'angle en A The proof of the pudding is in the eating. #9 - 12-03-2011 12:48:46#10 - 12-03-2011 15:15:17
Ti_1_glePlus qu'1 heure pour résoudre cette énigme... #11 - 12-03-2011 15:47:58
Tri_1g_leQuand je vois la simplicité de la réponse de franck9525, j'ai envie d'aller me pendre... Avoir quatre mains, c'est plus pratique pour taper sur un clavier. #12 - 12-03-2011 16:52:01#13 - 12-03-2011 19:15:23
Trri_1_gleOui bravo a ceux qui ont trouvé en utilisant uniquement les mathématiques. Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt Réponse rapideSujets similaires
Mots clés des moteurs de recherche
|
 | ||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | ||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.