Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 15-08-2011 13:53:16
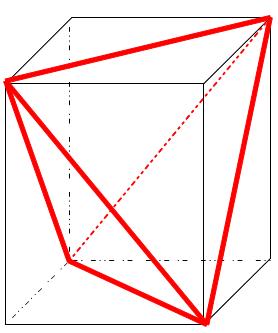
yétra-mathsOn donne un cube d'arête 1. Deux sommets d'un tétraèdre régulier sont situés sur la diagonale du cube, les deux autres sur la diagonale d'une face. Quel est le volume de ce tétraèdre ? C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#0 Pub#2 - 15-08-2011 14:19:19#3 - 15-08-2011 14:29:35
Tétr-mathsNon, Gwen. Il y a une seule position du tétraèdre régulier (pour une diagonale et une face du cube déterminées à l’avance) et par conséquent un seul volume possible. C'est à l'intelligence d'achever l'oeuvre de l'intuition. #4 - 15-08-2011 15:09:23#5 - 15-08-2011 17:36:30
tétea-mathsOk, j'ai mis plus de 5 minutes ... #6 - 16-08-2011 15:38:51#7 - 16-08-2011 16:34:27
TétramathsGrand bravo nodgim, ce n'était pas simple... C'est à l'intelligence d'achever l'oeuvre de l'intuition. Réponse rapideSujets similaires
Mots clés des moteurs de recherche
|
 | |||||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | |||||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.