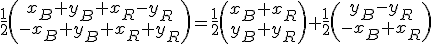Quelques sommes de vecteurs plus tard, et en appelant [latex]\left( \begin{matrix} x_B \\ y_B \end{matrix} \right)[/latex] les coordonnées de l'arbre bleu et [latex]\left( \begin{matrix} x_R \\ y_R \end{matrix} \right)[/latex] celles de l'arbre rouge, le trésor est aux coordonnées :
[TeX]\frac{1}{2} \left( \begin{matrix} x_B + y_B + x_R - y_R \\ -x_B + y_B + x_R + y_R \end{matrix} \right)[/TeX]
Oui, pendant le calcul, les coordonnées de la potence finissent par disparaître, ce qui semble cohérent avec l'énoncé du problème

Il me reste deux questions :

- comment exprimer ces coordonnées d'une façon géométrique plus facilement compréhensible ?

- pouvait-on parvenir au résultat en ne passant pas par des coordonnées, donc avec de la géométrie dans le plan toute simple ?

Autant dire que je vais continuer de réfléchir au problème...



Ebauche de réponse a la première question :
[TeX]\frac{1}{2} \left( \begin{matrix} x_B + y_B + x_R - y_R \\ -x_B + y_B + x_R + y_R \end{matrix} \right) = \frac{1}{2} \left( \begin{matrix} x_B + x_R \\ y_B + y_R \end{matrix} \right) + \frac{1}{2} \left( \begin{matrix} y_B - y_R \\ -x_B + x_R \end{matrix} \right)[/TeX]
La première des deux composantes de la somme correspond aux coordonnées du centre de [BR] : on va donc commencer par aller pile au milieu des deux arbres.

Après, euh... Je ne sais pas encore ^^

Mathias : La deuxieme composante représente une rotation vectorielle à DROITE d'un vecteur que tu dois trouver ... il ne reste plus qu'à conclure .
Jackv : Bonne réponse , il ne reste plus qu'a démontrer !

halloduda : tu es sur la bonne voie ... continue

Je ne comprends pas l'énoncé je pense ... Parce que j'arrive à des lieux différents suivant où j'imagine la potence . 

On le trouve à la pointe d'un triangle isocele de base  les deux arbres et de hauteur moitié.



pas sûr de ma droite et de ma gauche mais bon .

Elles figurent les égalités de distance, j'avais la flemme de tout annoter

En gros , ça dit que si a+b = x  alors (b-a) / 2 + a = x/2 
A et b étant les vecteurs vert et noir, x étant la distance entre les deux arbres.

On tourne à 90° et on a le même genre de système.

Conclusion, en absice  et en ordonnée on a x/2 quelle que soit  la potence. mais comme je suis un gros paresseux, j'ai résumé.

Sur la médiatrice du segment compris entre les deux arbres, à une distance du segment égale à la moitié de la distance entre les deux arbres, en tournant à droite (je sais, c'est pas très trigo comme expression, mais je m'inspire de l’énoncé !!!) en venant de l'arbre rouge depuis ce segment...

Pour la démonstration, je passerai plus tard !!! (un peu loin tout cela, je manque cruellement d'entrainement !)

Le point cherché est indépendant du point de départ et se trouve au centre du carré de côté [BR] situé sur la gauche lorsqu'on va de B à R.

Sympa ce petit problème

Presque tous les logiciens ont trouvé le bon point ... Maintenant la démonstration ! je vais compléter la démonstration de Mathias !
Sur un plan orienté; on considere :
- Le point P qui représente la potence
- Le point B qui représente l'arbre bleu
- Le point R qui représente l'arbre rouge
- le point I qui représente le 1er cale
- le point J qui représente le 2me cale.
- le point T qui représente le trésor.
On pose :
[TeX]\vec{PB} \binom{Xb-Xp}{Yb-Yp}[/TeX]
On sais que [latex]\vec{BI}[/latex] est une rotation vectorielle de [latex]\vec{PB}[/latex] d'un angle de -90°.
Du coup les coordonnées de [latex]\vec{BI}[/latex] sont :
[TeX]\vec{BI} : \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix}\binom{Xb-Xp}{Yb-Yp}[/latex] = [latex]\vec{BI}\binom{Yb-Yp}{-Xb+Xp}[/TeX]
Alors :
[TeX]\vec{PI} \binom{Xb-Xp+Yb-Yp}{Yb-Yp-Xb+Xp }[/TeX]
on peut tirer tout simplement les coordonnées de I (1er cale).
[TeX]I \binom{Xb+Yb-Yp}{Yb-Xb+Xp }[/TeX]
De la même manière , on trouve les coordonnées de J (2eme cale).
[TeX]J \binom{Xr-Yr+Yp}{Yr+Xr-Xp}[/TeX]
Avec ces données , on peut maintenant determiner les coordonnées de T :
[TeX]T : \frac{1}{2} \binom{Xb+Yb+Xr-Yr}{-Xb+Yb+Xr+Yr}[/TeX]
On a :


La première des deux composantes de la somme correspond aux coordonnées du centre de [BR]

par contre :
[TeX]\begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix}\binom{Xb-Xr}{Yb-Yr} = \binom{Yb-Yr}{-Xb+Xr}[/TeX]
Alors : la deuxieme composante représente la rotation vectorielle à droite d'un angle droit (-90°) du vecteur : [latex]\frac{1}{2}\vec{RB}[/latex].

CONCLUSION :
Le triangle TBR est isocèle (puique T appartient à la médiatrice de [BR]) et rectangle en T.

Merci à tous les participants

enfin une petite figure

Le passage par les complexes permettait de rendre la résolution encore plus simple, vu que la rotation se faisait sans faire intervenir de matrice de rotation. Bravo Hallo