Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 30-10-2011 17:42:55
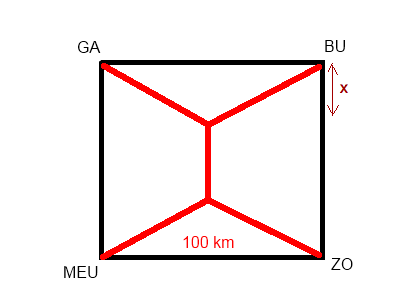
Réseau routier hadokienTout comme Clydevil je vous propose une énigme de minimisation d'un parcours routier. "L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#0 Pub#2 - 30-10-2011 18:02:35
Réseua routier ShadokienBonjour, #3 - 30-10-2011 18:28:34
réseau roytier shadokienUn petit article sur cet intéressant problème lié à celui de Steiner : http://apmeplorraine.free.fr/modules/probleme/PB53.pdf #4 - 30-10-2011 18:36:29#5 - 30-10-2011 18:40:34
Réseau routier ShadookienJe ne suis pas sûr du lien mais ça me rappelle un truc posté il y a peu... #6 - 30-10-2011 20:12:06#7 - 30-10-2011 20:28:23
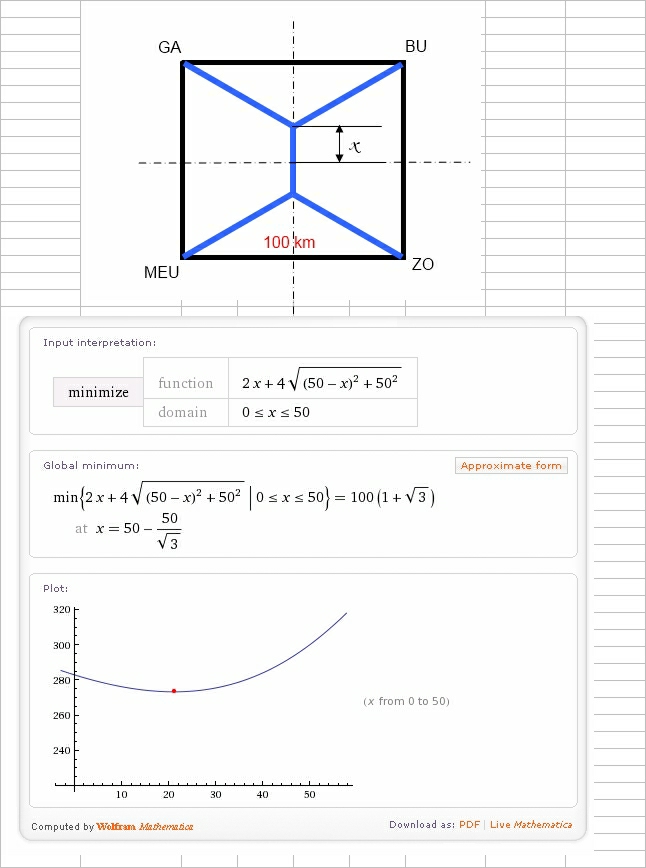
Réseau routier ShadokieenImaginons que GA et MEU soient reliées par un élastique ainsi que BU et ZO et que l'on cherche à rapprocher les centres de ces deux élastiques. En résolvant le problème d'optimisation de la distance totale, on s'aperçoit qu'il n'est pas nécessaire qu'ils se touchent (où l'on retrouverait alors la configuration diagonale) pour obtenir la distance totale minimale de [latex]100(1+\sqrt{3})[/latex]) soit 273 km. #8 - 30-10-2011 21:14:42
Réseau routier SadokienSentiment de déjà-vu... Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298 #9 - 30-10-2011 22:05:55
Réseau routier Shadokine
Tu veux dire les Steiner tree? :p #10 - 31-10-2011 00:58:24
réseau roitier shadokienJe donne la meme solution que pour clydevil, ce qui pour ton enigme donne 273.205080758 Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt #11 - 31-10-2011 06:28:45
Réseau routierr ShadokienBonjour, Il aurait pu pleuvoir, con comme il est ! (Coluche) #12 - 31-10-2011 07:10:26#13 - 31-10-2011 09:42:50
Réseau routie ShadokienJ'ai trouvé 273 en tracant un segment qui passe par le milieu de 2 côtés opposés et en prenant 1/4 de la longueur pou Un promath- actif dans un forum actif #14 - 31-10-2011 11:02:27
réseau routiee shadokienOn va imaginer un réseau qui serait composé d'une ligne droite de longueur X, située à 50 km au nord / au sud des villes; terminées par 4 lignes droites (de même longueur) qui relient une ville à l'extrémité de ligne la plus proche. #15 - 01-11-2011 02:54:09#16 - 01-11-2011 11:09:53
Résseau routier ShadokienA force de connaitre les énigmes par coeur vos réponses deviennent compendieuses. "L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline #17 - 01-11-2011 12:36:09
Réseau outier ShadokienVoila ce que je propose Quand les choses deviennent trop compliquées, il est parfois normal [...] de se demander : ai-je posé la bonne question ? #18 - 01-11-2011 14:41:46
Réseau rouiter ShadokienEn revanche la distance total de ton parcours : "L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline #19 - 01-11-2011 14:58:26
Réseau routier ShadkienJ'ai appris le mot "compendieux" aujourd'hui, comme quoi, ce post n'était pas si redondant que cela ! Il aurait pu pleuvoir, con comme il est ! (Coluche) #20 - 01-11-2011 17:27:30#21 - 02-11-2011 01:28:47#22 - 02-11-2011 11:40:20
réseau routier qhadokienje poste ce lien ici, car perso je n'ai jamais trop réfléchis sur les ellipses, et la j'y trouve une belle application #23 - 02-11-2011 13:33:37
Rseau routier ShadokienA la demande de certain joueurs les deux énigmes sur les réseaux routiers finiront en même, d'où un rajout d'heure pour celle-ci. "L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline #24 - 02-11-2011 14:31:52#25 - 03-11-2011 22:56:21
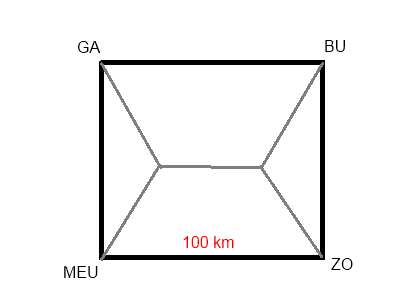
Réseau routie rShadokienLe réseau doit ressembler à ça : Réponse rapideSujets similaires
Mots clés des moteurs de recherche |
 | ||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | ||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.