|
#1 - 08-01-2013 22:45:10
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#2 - 08-01-2013 23:19:09
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
A umoins la moitié !
C'est du gâteau 
#3 - 09-01-2013 10:00:24
- SHTF47
- Imprnnçbl de Prs2Tt
- Enigmes résolues : 39
- Messages : 1629
- Lieu: Autre nom du colin
au moins ma moitié !
Raisonnement par l'absurde spotted.
La musique est une mathématique sonore, la mathématique une musique silencieuse. [Edouard HERRIOT]
#4 - 09-01-2013 11:29:37
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
au mouns la moitié !
Bah plus qu'à nous montrer 
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#5 - 09-01-2013 11:55:59
- godisdead
- Expert de Prise2Tete
- Enigmes résolues : 22
- Messages : 747
au moins la moirié !
Si on prend le cas le plus défavorable, tous les points sont sur la diagonale bas/gauche => haut/droit.
Tous les carrés remplissent la moitié de la figure (ex : la partie entre le coin en haut à gauche et la diagonale), est-ce que la surface occupée par les coins de chaque rectangle (ceux qui sont sous la diagonale) est supérieur au vide entre chaque rectangle déssiné ?
XXXXX
XXXXO
XXXOO
XXOOO
XOOOO
S'il y a 5 points, c'est evident, mais lorsque le nombre de points tend vers l'infini ?
#6 - 09-01-2013 14:24:10
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 239
Au moinns la moitié !
godisdead: Si on prend le cas le plus défavorable[...]
J'ai pensé aussi à ce cas là, mais je ne vois pas pourquoi c'est le plus défavorable 
#7 - 09-01-2013 16:46:30
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Au mins la moitié !
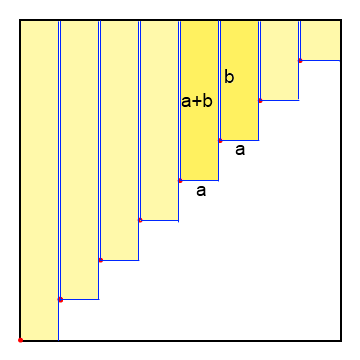
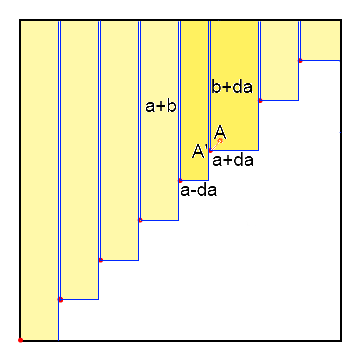
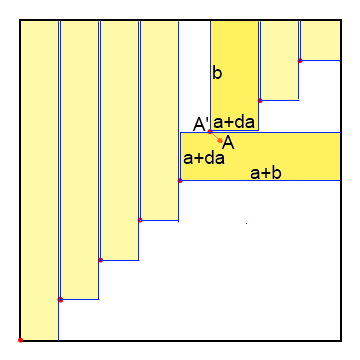
Il semble que pour [latex]n[/latex] points la borne inférieure de l'aire que l'on peut recouvrir serait [latex]\frac{n+1}{n}[/latex] ce qui correspond bien à [latex]n[/latex] points régulièrement répartis sur la diagonale .
Il faut prendre ça avec un gros conditionnel car je n'ai aucune certitude et bien sûr aucune preuve 
On peut tout à fait accepter que les rectangles aient des frontières communes , ça simplifie la vision des choses sans rien changer à la borne .
Vasimolo
#8 - 09-01-2013 17:14:10
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Au moins a moitié !
Oui j'ai également trouvé [latex]\frac{n+1}{n}[/latex] pour [latex]n[/latex] points régulièrement répartis sur la diagonale.
Reste à prouver que c'est le pire des cas...
#9 - 09-01-2013 17:24:45
- godisdead
- Expert de Prise2Tete
- Enigmes résolues : 22
- Messages : 747
ay moins la moitié !
Je n'ai pas les bases mathématiques pour le prouver, mais l'idée est que pour avoir le moins de surface pavé, il faut que chaque point se gène le plus possible.
Donc l'écart des coordonnées entre le point A(E;F) et le point B(R;S) doivent être minimum en X et en Y. (A et B étant deux points consécutifs)
Pour E=0 et F=0, on a R=S, et donc tous les points sont sur la diagonale.
#10 - 09-01-2013 17:46:36
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
au moins la moitué !
Il semble que le Latex du site ait de nouveau rendu l'âme , espérons que le problème ne nécessitera pas trop de calcul 
Je ne pense pas que le problème nécessite de grosses connaissances mathématiques , il s'agît plutôt de trouver un bon angle d'attaque ( plus facile à dire qu'à faire ) .
Vasimolo
#11 - 09-01-2013 18:10:27
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Au moins la moitié !!
Tiens! Je pensais que c'était "Domi" qui proposait cette énigme, et j'allais justement lui suggérer de la présenter ici.
ça fait déja plusieurs jours que j'y réfléchis et je n'ai pas de solution, malgré l'évidence de la chose...
#12 - 09-01-2013 18:15:31
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Au moins la moiité !
Imod , Domi , Vasimolo , ... , c'est selon la forme du gâteau .
Certains gâteaux conviennent à tout le monde alors autant les partager 
Vasimolo
#13 - 09-01-2013 18:24:24
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Au moisn la moitié !
J'ai bien remarqué que les problèmes que tu posais sur Math Forum étaient de même nature, mais c'est très curieux, je n'ai pas reconnu ta personnalité dans les 2 sites. Je te trouve ici moins émotif, un peu plus sur le recul, plus posé. Est ce à dire que nos personnalités évoluent en fonction du public ?
J'en suis encore tout retourné, de cette révélation...
#14 - 09-01-2013 18:27:38
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#15 - 09-01-2013 18:39:02
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Au moins la moiitié !
Je suis surtout plutôt surpris de cette cachotterie pas bien utile.
Mais bon, c'est pas bien grave. Je ne comprends pas, c'est tout.
#16 - 09-01-2013 18:48:49
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Au monis la moitié !
Ce ne sont pas des cachotteries quand je m'inscris sur un site je propose mon pseudo usuel et quand il est refusé j'en propose un deuxième , etc , ...
Je n'ai jamais caché ma participation à plusieurs sites , j'ai même fourni plusieurs liens de sujets que j'avais proposé en parallèle sur d'autres sites sous d'autres pseudos .
J'étais persuadé que tu m'avais reconnu mais comme tu dis ce n'est pas très grave .
Vasimolo
#17 - 10-01-2013 17:32:46
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3615
- Lieu: 94110
#18 - 10-01-2013 18:06:54
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
u moins la moitié !
Beaux dessins, mais pas très convaincants pour l'instant.
En mettant les points au hasard, on a des configurations bien plus compliquées.
#19 - 10-01-2013 19:41:53
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Au moisn la moitié !
Je peux me tromper mais il me semble qu'on peut évacuer les problèmes de limite , on est complètement dans le discret , c'est presque un problème d'échiquier . On peut supposer sans peine que tous les points sont aux nœuds d'un quadrillage orthonormé . On peut aussi évacuer les problèmes de contact entre les petits rectangles , si on arrive à faire plus que 1 avec contact on fera plus que 1 sans contact . Bref on a un échiquier avec des coins inférieurs-gauches imposés et il faut faire un pavage rectangulaire qui recouvre au moins la moitié de l'échiquier .
C'est plus facile à visualiser mais apparemment pas plus simple à résoudre 
Content de voir que le problème vous plait 
Vasimolo
#20 - 10-01-2013 19:52:09
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Au monis la moitié !
C'est amusant, mais je me suis fait les même réflexions que vous tous, avec les même erreurs au départ.
La représentation sous le bon angle reste cependant compliqué à trouver... s'il existe !
#21 - 10-01-2013 20:02:55
- godisdead
- Expert de Prise2Tete
- Enigmes résolues : 22
- Messages : 747
au moons la moitié !
On peut aussi évacuer les problèmes de contact entre les petits rectangles , si on arrive à faire plus que 1 avec contact on fera plus que 1 sans contact .
Non, je ne suis pas d'accord. Comme vu plus haut par Jackv.
Lorsque le nombre de points tend vers l'infini, la formule reste vrai à condition que la distance entre 2 bandes soit toujours infiniment plus petite que la largeur d'une bande.
Ce qui devient douteux à la limite, lorsque la largeur d'une bande tend vers zéro ! Sauf si on accepte, comme le propose Vasimolo que les rectangles aient des frontières communes.
Prenons un exemple physique :
Sur un carré de 10 cm de coté, tu mets des points sur la diagonale espacée de 1 mm (voir 0.5 mm), et tu essayes sans que les rectangles se touchent de remplir plus de la moitié de ton carré !
#22 - 10-01-2013 20:07:51
- godisdead
- Expert de Prise2Tete
- Enigmes résolues : 22
- Messages : 747
au moins la loitié !
Un autre angle d'attaque pourrait être, soit un carré 100 * 100.
10 000 points, je peux remplir tout le carré. Pour chaque point que je supprime, quelle surface je laisse vide ?
Est-ce qu'en enlevant un grand nombre de point, j'arriverais à laisser 5000 carrés vides ?
Est-ce que le cas d'un carré 2*2 ou 3*3 permet de généraliser à N*N ?
Je creuserais ça dès que ma fille sera au lit !
#23 - 10-01-2013 20:30:41
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
au moinq la moitié !
godisdead a écrit:On peut aussi évacuer les problèmes de contact entre les petits rectangles , si on arrive à faire plus que 1 avec contact on fera plus que 1 sans contact .
Non, je ne suis pas d'accord. Comme vu plus haut par Jackv.Lorsque le nombre de points tend vers l'infini, la formule reste vrai à condition que la distance entre 2 bandes soit toujours infiniment plus petite que la largeur d'une bande.Ce qui devient douteux à la limite, lorsque la largeur d'une bande tend vers zéro !
Pas d'accord avec le désaccord  . .
Les deux limites n'évoluent pas en même temps , on fixe un nombre de points très grand si on veut , mais une fois donné il ne bouge plus puis on affine l'espace entre les rectangles donc contact ou pas contact , le problème est le même .
Vasimolo
#24 - 10-01-2013 20:57:55
- godisdead
- Expert de Prise2Tete
- Enigmes résolues : 22
- Messages : 747
Au moins la moitéi !
Pas d'accord avec le pas d'accord avec le désaccord 
A partir de ma théorie (les points sur la diagonale), le problème se resume à déterminer si l'aire du triangle sous la diagonale de chaque rectangle est plus grande ou plus petite que le vide entre ce rectangle et le suivant.
La tolérance de vide entre deux rectangles est une constante. Une fois que cette constante est déterminé, tu pourras determiner à partir de combien de points tu n'arriveras plus à remplir la moitié de ton carré !
#25 - 10-01-2013 21:39:40
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
au moins la moiyié !
A dire vrai je n'ai pas regardé ta théorie en détail , le nombre de point étant fixé , si on peut faire plus que 1 en acceptant les contacts , on peut faire plus que 1 en les approchant , c'est une évidence topologique 
Vasimolo
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum