Salut Hallodula,

Tu pourrais préciser l'énoncé ? est-ce "une personne se trouvant sur l'un des côtés ...

- ne peut voir aucun des trois autres côtés dans sa totalité (mais un bout de chaque ok)
- ne voit rien du tout des 3 autres côtés
- ne voit pas les 3 côtés intégralement (mais 2 plus un bout ok)
- ne voit pas un bout de chaque côté (mais un bout de deux d'entre eux ok)

Merci d'avoir précisé.

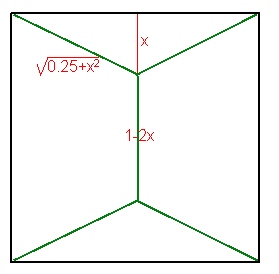
Il me semble que la meilleure disposition des haies devrait être celle-ci :

La longueur des haies devient alors :
[TeX]4\sqr{0.25+x^2}+ 1-2x[/TeX]
Cette fonction admet un minimum pour x = 0.289,
ce qui conduit à une longueur de haie de 273.2 m.

Malheureusement, cette valeur ne valide pas la case réponse. 
Où est l'erreur ??? 

On va poser P poteaux et relier ensemble ces poteaux par des haies.
Il est clair qu'il faut au moins un poteau à chaque coin du pré, sinon on pourra d'un côté apercevoir un peu du côté adjacent.

Une condition suffisante (mais pas nécessaire) pour résoudre le problème est que le graphe des haies soit connexe, et alors on sait (d'une précédente énigme) que la solution optimale est l'arbre de Steiner pour un carré, pour une longueur totale de haies de [latex]1+\sqrt{3}\sim 2.732[/latex] hm, soit 273.2 m.

Mais visiblement c'est pas ça et il y a mieux, avec une solution non-connexe. Mais je ne vois pas où je pourrai faire un trou dans mes haies, sans soit rallonger la longueur totale, soit laisser voir un côté.

Un petit indice sera bienvenu... je sèche complètement.

En trafiquant un carré avec ses deux diagonales, j'ai en effet trouvé mieux, mais pour l'instant aucune idée de prouver que c'est LE mieux.

Le croquis montre l'idée, les haies sont les traits rouges.

Du coup pour les segments [latex]AF,CF[/latex] et [latex]DF[/latex], on prend l'arbre de Steiner du triangle [latex](A,C,D)[/latex], donc les angles [latex](A,F,D), (D,F,C), (A,F,C)[/latex] font [latex]2\pi/3[/latex], on en déduit [latex]ECF=\pi/6[/latex], et comme [latex]CE=\sqrt{2}/2[/latex], après avoir demandé à Pythagore, on trouve comme longueur totale : [latex](\sqrt{3}+2)/\sqrt{2}[/latex] hm soit environ [latex]263,9[/latex] m.


NB : c'est facile d'être un as de Geogebra... simple et génial comme logiciel !