|
#1 - 29-05-2012 00:10:42
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#2 - 29-05-2012 10:34:23
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
evhecs 11
M'est avis que l'on peut toujours se débrouiller pour rassembler tous les robots sur une même case, typiquement (pour des raisons pratiques) un des coins de la grille, tant que le labyrinthe est "connexe", c'est-à-dire qu'il existe un chemin entre deux cases quelconques. Plus qu'à les bouger tous en même temps par la suite, et hop.
J'attends mon eureka (ou bien que tu donnes un indice sur une piste de preuve  ) )
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#3 - 29-05-2012 15:49:29
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 239
EEchecs 11
Bonjours,
Je suppose que quand un robot arrive au hangar il disparait et qu'il ne peut plus en sortir (sinon il pourrait y avoir des problèmes de superposition).
On suppose aussi qu'il existe toujours un chemin de la position initiale d'un robot au hangar.
Dans ce cas je vais donner une méthode pour ranger un robot:
On choisi un des robots au hasard, on choisie un chemin menant au hangar, on lui fait suivre ce chemin. Si à une étape il est bloqué par un autre robot, c'est que ce dernier est sur la position suivante du chemin, on échange alors alors le robots à mener à l’objectif avec celui qui bloque.
Par ce procédé, à chaque étape on se rapproche d'une case du hangar, on y mènera donc toujours un robot.
A la fin, il existera encore des chemin menant les robots restant vers le hangar (par exemple le chemin inverse parcourus puis le chemin initiale).
Ainsi, on peut mener un à un des robot vers le hangar.
Il est même très facile de programmer la procédure, si on possède l'algorithme pour trouver un chemin d'un robot au hangar.
Mathieu.
#4 - 29-05-2012 18:02:48
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
rchecs 11
@Mathias : Spoiler : [Afficher le message] c'est la bonne méthode , on peut juste expliciter un peu plus la première étape .
@Mathieu : Spoiler : [Afficher le message] non , le hangar est une case de passage comme une autre ( je te rappelle que plusieurs robots peuvent partager la même case ) .
Bon courage à ceux qui cherchent 
Vasimolo
#5 - 29-05-2012 18:15:06
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,194E+3
zchecs 11
A partir du moment où on peut "regrouper" deux robots quelle que soit leur position, on peut en grouper 3 puis 4, et enfin aller les garer.
Il suffit alors de travailler avec les butées.
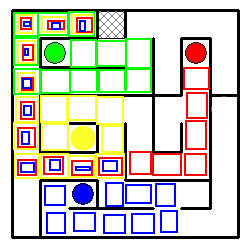
Dans l'exemple :
G BBBB DDDDDD et le jaune est confondu avec le bleu en bas à droite
Puis
GG H GG HHH D on attrape le rouge
Et
G BB GGG HHH DDDD B on a le vert
Et enfin : H G H Tout le monde est garé. (Enfin, si j'ai bien compris le problème.)
Gwen.
#6 - 29-05-2012 18:20:24
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Eches 11
Bon je ne répondrai pas, je connais. Mais c'est bien rigolo ce truc !
#7 - 29-05-2012 18:25:54
- freedomAO
- Habitué de Prise2Tete
- Enigmes résolues : 49
- Messages : 12
- Lieu: Vottem; Liège; Belgique.
evhecs 11
oui c'est possible; il suffit d'amener 2 robots sur la même case
puis 3, puis 4, puis les 4 dans le hangars.
#8 - 29-05-2012 19:08:30
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 239
Echecs 1
Je ne sais pas pourquoi j'avais lu l'inverse de la remarque 1 
Puisque on peut superposer les robots, il serait intéressant de tous les superposer et le problème deviendrait trivial.
Pour superposer deux robots c'est très simple, il suffit de choisir un des deux robots et de l'amener sur l'autre, ça marchera toujours pourvu que le labyrinthe soit borné.
preuve : Considérons le chemin initiale menant du robot choisi au second, comme une liste de déplacement.
Partie 1: décroissance
A chaque déplacement le premier élément de la liste est retiré et on l’effectue avec la télécommande. Dans le pire des cas il faut rajouter ce déplacement à la fin de la liste pour rejoindre le robot cible, si ce dernier s'est aussi déplacé.
Donc le nombre d'élément de la liste est décroissant.
Partie 2: décroissance stricte
Considérons le vecteur V de séparation pour passer d'un robot à l'autre "à vole d'oiseau" (par exemple 3 case vers le bas 2 vers la gauche).
Quand le robot poursuivant aura atteint la position initiale du robots cible,
il y a deux cas:
_Soi le robots cible a rencontré un obstacle, auquel cas la liste de déplacement s'est réduite.
_Sinon le robot cible s'est toujours déplacer comme le poursuivant, le vecteur V de séparation est resté constant.
Or le labyrinthe est borné donc le robot cible ne pourra pas s'échapper éternellement en parcourant V, 2V, 3V, 4V... il finira par être bloqué par un coin.
Conclusion : la listes des déplacements à effectuer pour rassembler les robots est strictement décroissante, il finiront par se rejoindre. CQFD
Mathieu.
#9 - 29-05-2012 19:36:05
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Echecs 1
Que du bon !!!
On peut considérer ça comme un échauffement pour la suite 
La partie "1 peut rejoindre 2 en le bloquant sur un bord ou dans un coin" mérite quand même ( à mon goût ) d'être un peu détaillée ( Bravo Mathieu ! ) .
Pour ceux qui cherchent encore , l'idée est simple !
Vasimolo
#10 - 29-05-2012 20:08:32
- elpafio
- Elite de Prise2Tete
- Enigmes résolues : 43
- Messages : 1018
Echec s11
Une illustration d'un rangement de robots en 34 mouvements.
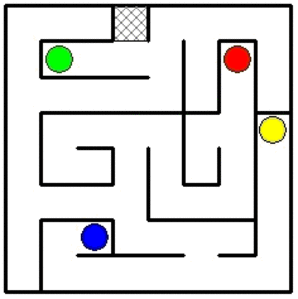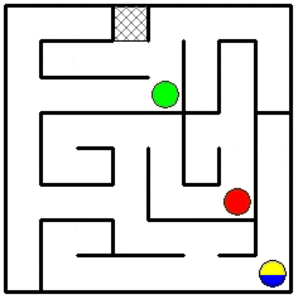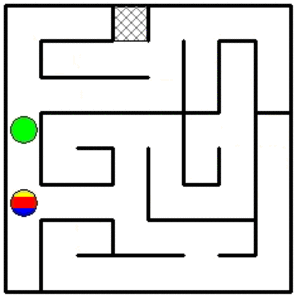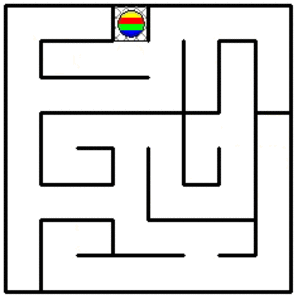
Il est possible qu'on puisse faire plus court car je n'ai pas cherché à optimiser.
Merci pour le challenge 
#11 - 29-05-2012 21:29:52
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
rchecs 11
Salut!
A l'occasion de celui ci:
Programmation robotique aveugle
Je m’étais posé la question jusqu'à me convaincre que c’était toujours faisable quelque soit le labyrinthe. Seulement vu la difficulté que j'ai eu a retrouver une démonstration juste et propre ça devait être du feeling.
Finalement ce soir j'ai trouvé la démonstration suivante:
On considère deux robots Alice et Bob, Bob voulant se superposer avec Alice (esprit salace s'abstenir)
Bob fait une certaine séquence d'actions S0 pour aller ou se trouvait Alice avant qu'il ne bouge.
Pendant qu'il a fait S0 Alice à réalisé la séquence effective S1 (effectif car on l'a nettoyé des éventuelles actions passives).
Bob va ensuite réaliser lui même S1 (ce qui rejoins la case ou se trouvait Alice juste avant q'uil ne démarre cette manœuvre) et on note S2 la séquence effective réalisée pendant le même temps par Alice.
Etc...
En nombre d'actions on remarque que Actions(S(n+1)) <= Actions(S(n))
Ainsi donc la suite d'entiers positifs Actions(S(n)) converge.
Comme on a S(n+1) inclus dans S(n) ceci veut dire que Bob fini par répéter indéfiniment la même séquence SK.
A vol d'oiseau SK correspond à une translation nulle sinon elle ne pourrait être réalisée indéfiniment au sein d'une enceinte bornée.
Ce qui veut dire qu'au moment ou Bob fait SK il est déjà superposé avec Alice.
A partir de là si on peut superposer deux robots on peut en superposer N et une fois superposés on peut les mettre ou on le désire.
CQFD.
#12 - 29-05-2012 21:57:17
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
echecq 11
Bonjour à tous,
On peut ramener un problème à N robots à une partie à 2 robots. En effet, pour passer de N à N-1, il suffit de faire partager la même case à 2 robots. Pour arriver à cela, je dessine le chemin entre ces 2 robots, et, en bloquant l'un ou l'autre sur une cloison, je diminue la distance entre eux jusqu'à ce qu'il se rejoignent.
Bonne soirée.
#13 - 29-05-2012 22:43:07
- langelotdulac
- Ange de Prise2Tete
- Enigmes résolues : 49
- Messages : 2963
- Lieu: Paradis
Echecs 1
Tu es largement assez dingo pour qu'un Minito te semble cohérent \o/ !
#14 - 29-05-2012 22:57:27
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Echeecs 11
Elpatio : Chapeau pour l'animation !!!!!
Langelot : L’essentiel est de participer 
Bravo aux autres .
Un petit challenge pour les amateurs : le minimum de manip pour ranger tous les robots avec l'exemple proposé ???
Vasimolo
#15 - 29-05-2012 23:22:32
- irmo322
- Professionnel de Prise2Tete
- Enigmes résolues : 36
- Messages : 203
echecd 11
Proposition: Quelque soit le labyrinthe (fini), s'il existe un chemin allant du robot rouge au robot vert, alors on peut avec une seule télécommande faire rejoindre les deux robots.
Corollaire: Quelque soit le labyrinthe, quelque soit le nombre (fini) de robot, s'ils sont connectés, alors on peut avec une seule télécommande les faire rejoindre.
Corollaire: Quelque soit le labyrinthe, quelque soit le nombre (fini) de robot, s'ils sont connectés à la case hangar, alors on peut les amener avec une seule télécommande à la case hangar.
J'ai toujours eu envie d'écrire des trucs comme ça... 
#16 - 29-05-2012 23:31:30
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
echecd 11
J'ouvre les "hostilités":
- GBBBB: bleu et jaune sont en bas,
- DDDDDD: bleu a rejoint jaune,
- GGGHHGGHHHGG: bleu/jaune a rejoint rouge,
- DDBBGGGHHHDDDDHH: bleu/jaune/rouge a rejoint vert,
- BGH: bleu/jaune/rouge/vert est au garage.
J'en suis à 42 coups: qui dit mieux ?
A+
#17 - 30-05-2012 17:50:27
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Echecs 111
J'ai ajouté , dans le message initial , un palmarès pour le minimum de déplacements avec la position proposée .
Vasimolo
#18 - 30-05-2012 22:42:26
- Moriss
- Professionnel de Prise2Tete
- Enigmes résolues : 37
- Messages : 460
checs 11
En 35 mvts.
1) Je fusionne Bleu et Jaune :
← ↓↓↓↓ → → → → → →
Rouge est donc descendu en bas de sa colonne, Vert est tout à droite de son couloir.
2) Je fusionne Bleu/jaune avec Rouge :
← ← ↑ ← ↑ ← ↓↓↓
Vert est alors tout à gauche de son couloir.
3) Je les fusionne avec Vert :
↑ ← ← ← ↑↑↑ → → → → ↓
4) Je range tout le monde dans le hangar :
↑ ← ↑
5) et maintenant, je cherche où j'ai rangé ces foutues télécommandes !

#19 - 30-05-2012 23:16:27
- langelotdulac
- Ange de Prise2Tete
- Enigmes résolues : 49
- Messages : 2963
- Lieu: Paradis
Ehecs 11
Langelot : L’essentiel est de participer
Ca sent pas bon ça ! 
Tu es largement assez dingo pour qu'un Minito te semble cohérent \o/ !
#20 - 30-05-2012 23:17:27
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
exhecs 11
@Morris : Spoiler : [Afficher le message] il me semble que tu as zappé quelques touches
Vasimolo
#21 - 30-05-2012 23:17:32
- Moriss
- Professionnel de Prise2Tete
- Enigmes résolues : 37
- Messages : 460
Echcs 11
J'ai édité mon message : je n'ai trouvé qu'une touche manquante (désolé).
#22 - 31-05-2012 10:54:16
- Corsaire
- Amateur de Prise2Tete
- Enigmes résolues : 27
- Messages : 7
Echecss 11
37 en faisant:
mettre le bleu en bas à droite, le jaune le rejoint, on les fait remonter vers le rouge, qui les rejoints tout à gauche, un fusionne avec le vert et les 4 vont se ranger:
GAUCHE
BAS
DROITE 6
BAS 3
GAUCHE 2
HAUT
GAUCHE 2
HAUT 1
GAUCHE
BAS 2
GAUCHE 3
HAUT 5
BAS 2
DROITE 4
HAUT
GAUCHE
HAUT
Premier essai à chaud.. j'y réfléchi plus longtemps.. :p
#23 - 31-05-2012 11:05:44
- Corsaire
- Amateur de Prise2Tete
- Enigmes résolues : 27
- Messages : 7
rchecs 11
Autre méthode, jaune et rouge descendent, jaune rejoint par le bleu, puis rejoignent le rouge qui rejoignent le vert.. mais tjs 37 mouvements.. 
Bas 4
Gauche 2
Bas 1
DROITE 6
Gauche 2
HAUT 2
GAUCHE
BAS 3
GAUCHE
HAUT
GAUCHE 3
HAUT 3
DROITE 2
HAUT
DROITE 2
HAUT
GAUCHE
HAUT
#24 - 31-05-2012 11:38:40
- ThomasLRG
- Habitué de Prise2Tete
- Enigmes résolues : 41
- Messages : 31
rchecs 11
Je trouve 34 aussi :
G Bx4 Dx6 Gx2 Hx2 G Bx2 G H Gx3 Hx3 Dx4 B H G H
#25 - 31-05-2012 15:07:38
- thefinder
- Amateur de Prise2Tete
- Enigmes résolues : 31
- Messages : 4
evhecs 11
Bonjour en 35 coups
1 gauche 4 bas 6 droite (jaune et bleu confondus)
2 gauches 2 haut 1 gauche 1 bas 1 gauche 2 bas (3 confondus)
1 haut 3 gauche 3 haut 3 droite 1 haut (vert dans la zone grise)
1 droite 1 haut 1 gauche 1 haut (fini).
Je ne vois pas comment on peut faire 34 coups?
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum