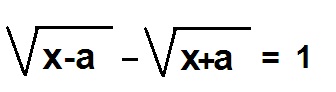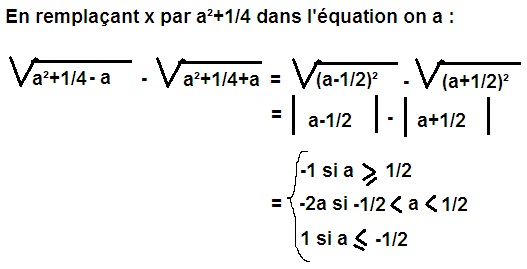|
#1 - 03-10-2012 22:51:07
- gilles355
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 421
une éqyation sympathique !
Bonjour,
Ce n'est pas une énigme mais une équation que j'ai trouvé intéressante avec une méthode de résolution originale.
Le niveau est 1ère S.
Voici l'équation :
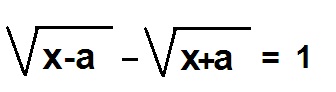
A la base l'équation avait a=1 mais étant donné qu'on peut généraliser 
j'ai mis la réponse sous la forme d'un entier suivi d'une fraction.
Edit: finalement j'enlève le temps pour qu'on puisse discuter
#2 - 03-10-2012 23:28:57
- Klimrod
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 4054
- Lieu: hébesphénorotonde triangulaire
une équation sylpathique !
Bonsoir,
(a) [latex]racine(x-a) - racine(x+a) = 1[/latex]
On retient que x >= a et x >= -a. Puis on multiplie par [latex]racine(x-a) + racine(x+a)[/latex] :
(b) [latex](x-a) - (x+a) = racine(x-a) + racine(x+a)[/latex]
On additionne (a) + (b) :
(c) [latex]-racine(x+a) -2a = 1 + racine(x+a)[/latex]
(d) [latex]2 racine(x+a) = -2a - 1[/latex]
On note que a <= -1/2, puis on élève au carré :
(e) [latex]x+a = (-a-1/2)^2[/latex]
On en conclut que :
(f) [latex]x = a^2 +1/4[/latex] (avec les conditions sur a <= -1/2)
Klim.
J'ai tant besoin de temps pour buller qu'il n'en reste plus assez pour bosser. Qui vit sans folie n'est pas si sage qu'il croit.
#3 - 03-10-2012 23:41:43
- franck9525
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1935
- Lieu: 86310
Ue équation sympathique !
x-a=1+x+a+2 rac(x+a)
x+a=(-a-1/2)^2=a^2+a+1/4
x=a^2+1/4
si a=1 alors x=5/4
dans l'hypothèse où il y a une erreur dans l'enoncé: ...=-1
The proof of the pudding is in the eating.
#4 - 03-10-2012 23:52:53
- Nombrilist
- Expert de Prise2Tete
- Enigmes résolues : 10
- Messages : 568
Une équation sypmathique !
Je trouve un truc bizarre: x = a² +1/4, à la condition que a soit inférieur ou égal à -1/2. Si a est supérieur à 1/2, alors le membre de gauche vaut -1.
#5 - 04-10-2012 09:01:05
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Une équation sympathiquue !
Conditions: il faut que x>=-a et que a<=0
On aura: V(x-a) - V(x+a) = 1 ==> [V(x-a) - V(x+a)]² = 1 ==> 2x - 1 = 2V(x²-a²)
==> 4x² - 4x + 1 = 4x² - 4a² ==> x = a² + 1/4 (que je n'arrive pas à valider  ) )
On peut vérifier que:
V(a² - a + 1/4) - V(a² + a + 1/4) = |a – 1/2| - |a + 1/2| = - a + 1/2 + a + 1/2 = 1
Edit: modifié: x>=-a (et pas a)
#6 - 04-10-2012 12:37:24
- gilles355
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 421
Une quation sympathique !
Klimrod a écrit:Bonsoir,
(a) [latex]racine(x-a) - racine(x+a) = 1[/latex]
On retient que x >= a et x >= -a. Puis on multiplie par [latex]racine(x-a) + racine(x+a)[/latex] :
(b) [latex](x-a) - (x+a) = racine(x-a) + racine(x+a)[/latex]
On additionne (a) + (b) :
(c) [latex]-racine(x+a) -2a = 1 + racine(x+a)[/latex]
(d) [latex]2 racine(x+a) = -2a - 1[/latex]
On note que a <= -1/2, puis on élève au carré :
(e) [latex]x+a = (-a-1/2)^2[/latex]
On en conclut que :
(f) [latex]x = a^2 +1/4[/latex] (avec les conditions sur a <= -1/2)
Klim.
On additionne (a) + (b) :
(c) 2racine(x-a) = -2a + 1
(d) racine(x-a) = -a + 1/2
(e) x-a = (-a+1/2)^2
On en conclut que :
(f) x = a^2 +1/4
#7 - 04-10-2012 12:43:49
- Klimrod
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 4054
- Lieu: hébesphénorotonde triangulaire
Une équation smpathique !
@Gilles :
Non, je maintiens ce que j'ai écrit !
Mais ta façon de faire permet également de conclure (de mon point de vue, tu as fait (a) - (b) )

J'ai tant besoin de temps pour buller qu'il n'en reste plus assez pour bosser. Qui vit sans folie n'est pas si sage qu'il croit.
#8 - 04-10-2012 13:52:56
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
Unne équation sympathique !
C'est sur le point (f) que je vais râler.
Il ne faut pas respecter [latex]x \ge 0[/latex] mais [latex]x \ge a[/latex] (pour l'existence des racines carrées de l'énoncé), d'une part.
Ensuite, [latex]x \ge a \Leftrightarrow \left( a² + \frac{1}{4} \right) \ge a \Leftrightarrow \left( a - \frac{1}{2} \right)^2 \ge 0[/latex]
Respecté pour tout a.
Mais ce qu'a énoncé Nombrilist
Nombrilist a écrit:Je trouve un truc bizarre: x = a² +1/4, à la condition que a soit inférieur ou égal à -1/2. Si a est supérieur à 1/2, alors le membre de gauche vaut -1.
est toujours valide, donc infirme ce que nous avons fait...
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#9 - 04-10-2012 15:03:58
- gilles355
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 421
Une équatio nsympathique !
Je viens de comprendre l'histoire du -1, j'ai tout simplement fais une erreur dans l'énonce que je corrige tout de suite.
L'équation est racine (x+a) - racine (x-a) = 1.
#10 - 04-10-2012 15:45:34
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Une équation sympathique !!
Bof ! Il suffit de remplacer a par -a et cela marche.
En fait il faut garder à l'oeil que V(x²)=|x| (et pas x).
Et donc, si x<O, alors V(x²)=-x.
#11 - 04-10-2012 16:26:51
- Klimrod
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 4054
- Lieu: hébesphénorotonde triangulaire
Une équation smypathique !
MthS-MlndN a écrit:C'est sur le point (f) que je vais râler.
Il ne faut pas respecter [latex]x \ge 0[/latex] mais [latex]x \ge a[/latex] (pour l'existence des racines carrées de l'énoncé), d'une part.
Ensuite, [latex]x \ge a \Leftrightarrow \left( a² + \frac{1}{4} \right) \ge a \Leftrightarrow \left( a - \frac{1}{2} \right)^2 \ge 0[/latex]
Respecté pour tout a.
Mais ce qu'a énoncé Nombrilist
Nombrilist a écrit:Je trouve un truc bizarre: x = a² +1/4, à la condition que a soit inférieur ou égal à -1/2. Si a est supérieur à 1/2, alors le membre de gauche vaut -1.
est toujours valide, donc infirme ce que nous avons fait...
@Mathias : sauf votre honneur, dans l'énoncé initial il faut que a ≤ -1/2.
La preuve : si tu choisis a = 0, tu n'auras pas de solution.
Et a ≤ -1/2 est la seule condition nécessaire et suffisante pour qu'on trouve une solution qui est x = a² + 1/4.
La condition x ≥ a est évidemment vraie, puisque a est supposé négatif et que x est évidemment positif.
La condition x ≥ -a est également implicitement vraie, car a² + a + 1/4 ≥ 0 pour tout a.
J'ai tant besoin de temps pour buller qu'il n'en reste plus assez pour bosser. Qui vit sans folie n'est pas si sage qu'il croit.
#12 - 05-10-2012 12:29:06
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
ine équation sympathique !
Klimrod a écrit:Dans l'énoncé initial il faut que a ≤ -1/2.
Comment arrive-t-on à cette condition ?
(Et laisse tomber cette histoire d'honneur, ça fait longtemps que je n'en ai plus  ) )
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#13 - 05-10-2012 15:27:19
- gilles355
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 421
Une équation sympathiqu e!
Vous êtes ok avec ça ?
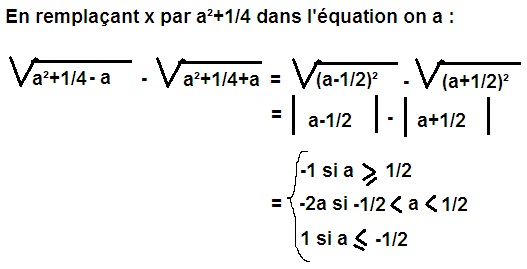
#14 - 05-10-2012 15:55:03
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Une équationn sympathique !
MthS-MlndN a écrit:Comment arrive-t-on à cette condition [latex]a \leq -\frac 12[/latex] ?
Je reprends le raisonnement de Klimrod, en le trafiquant un peu :
(a) [latex]\sqrt{x-a} - \sqrt{x+a} = 1[/latex]
Notons que l'équation n'a de sens que pour [latex]x \geq a[/latex] et [latex]x \geq -a[/latex].
On multiplie l'équation par [latex]1 + \sqrt{x-a} + \sqrt{x+a}[/latex] et l'on obtient après simplification :
(d) [latex]\sqrt{x+a} = -a - 1/2[/latex]
Notons qu'une condition nécessaire pour avoir une solution est [latex]-a -1/2 \geq 0[/latex], c'est-à-dire [latex]a \leq -1/2[/latex].
Puis on élève au carré :
(e) [latex]x+a = (-a-1/2)^2[/latex]
On en conclut que :
(f) [latex]x = a^2 +1/4[/latex]
On vérifie que dans ce cas, l'on a bien [latex]x \geq a[/latex] et [latex]x \geq -a[/latex].
Ce qu'il faut voir, c'est que ce raisonnement ne peut se remonter comme ça, toutes les étapes ne sont pas équivalentes :
Certes (a) [latex]\Leftrightarrow[/latex] (d) et (e) [latex]\Leftrightarrow[/latex] (f) sans problème.
Cependant (e) [latex]\Rightarrow[/latex] (d) seulement si [latex]-a -1/2 \geq 0[/latex], c'est-à-dire si [latex]a \leq -1/2[/latex].
En effet, [latex]A^2=B^2 \Rightarrow A=B[/latex] seulement si [latex]A[/latex] et [latex]B[/latex] sont de mêmes signes.
On voit donc que pour [latex]a \leq -1/2[/latex], on a une unique solution qui est [latex]x = a^2 +1/4[/latex].
Et dans le cas où [latex]a > -1/2[/latex], il n'y a pas de solution.
#15 - 05-10-2012 16:27:15
- Klimrod
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 4054
- Lieu: hébesphénorotonde triangulaire
Une équation sympahtique !
Voilà qui est bien reformulé ! Merci !

J'ai tant besoin de temps pour buller qu'il n'en reste plus assez pour bosser. Qui vit sans folie n'est pas si sage qu'il croit.
#16 - 06-10-2012 13:14:43
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
Une équation sympahique !
En effet 
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
Mots clés des moteurs de recherche
|
 |
|
Prise2Tete
Forum
Statistiques
Liste des membres
Hall of Fame
Contact
|

 Accueil
Accueil
 Forum
Forum