 |
#1 - 03-11-2012 14:00:28
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
patcours en vtt
Pour fêter mon 1000è message, voici un petit problème d'optimisation que j'ai recons- titué sur de lointains souvenirs et que j'avais alors trouvé très instructif. Je n'ai pas vu de sujet similaire sur le site: je suis désolé si j'ai mal cherché.
Avec mon VTT, je me trouve au point A d'un champ rectangulaire ABCD et je souhaite me rendre le plus vite possible au point C diagonalement opposé à A.
Ce champ, sur lequel mon VTT roule à 18 km/h, mesure 26 km de long sur 12 km de large et il est bordé sur le grand côté AB par une route en bonne état qui me permet d'avancer à 30 km/h.
Si je coupe par la diagonale, je vais mettre 60xV(26²+12²)/18 = (20/3).V205, soit plus de 95 mn. Si je choisis de prendre la route, puis de rejoindre le point C perpendiculai- rement à cette route, le temps nécessaire sera de 60x(26/30+12/18) = 92 mn, ce qui est un peu mieux.
Mais je suis vraiment pressé et j'ai trouvé un chemin qui me permet d'aller au point C en un temps minimum. Quel est la durée de mon parcours ?
La case-réponse valide la solution exprimée en mn.
Bon amusement (cette dernière expression n'est pas de moi  ) )
#2 - 03-11-2012 14:57:36
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,192E+3
Paarcours en VTT
Pour minimiser, il faut choisir x le début du trajet sur la route
x/30+ rac(820-52x+x^2) /18
Dérivée :
1/30 + (x-26)/18rac(820-52x+x^2) =0
Et là, merci wolfram  minimum pour x = 17km minimum pour x = 17km
Soit 84 mn
#3 - 03-11-2012 16:41:07
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Parcour en VTT
Salut !
Bon, si je ne m'abuse, en posant x la distance à B de [AB] où je quitte la route il faut trouver le minimum de la fonction :
f(x)=60(26-x)/30+60√(x²+12²)/18 = 52-2x+10√(x²+144)/3
f'(x)=-2+10x/[3√(x²+144)]
f'(x)=0 => 9(x²+144)=25x²
x²=81
Donc en quittant la route après 26-9=17 km, on obtient :
T=60(26-9)/30+60√(9²+12²)/18 = 84 minutes, ce qui est en effet bien mieux !
#4 - 03-11-2012 18:07:05
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
parcours rn vtt
Bonjour et bravo pour ton 1000ème 
Si on note [latex]26-x[/latex] la distance parcourue sur la voie rapide , la durée totale [latex]t[/latex] du trajet en heures est donnée par [latex]90.t=78-3x+5\sqrt{x^2+144}[/latex] cette fonction atteint son minimum pour [latex]x=9[/latex] ce qui donne [latex]60.t=84[/latex] .
84 minutes pour le trajet complet .
Vasimolo
#5 - 03-11-2012 19:41:55
- gilles355
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 421
Parccours en VTT
Salut,
C'est un super exercice que l'on peut donner à un élève de 1ère S voir de terminale S en début d'année.
Voici la solution détaillée :
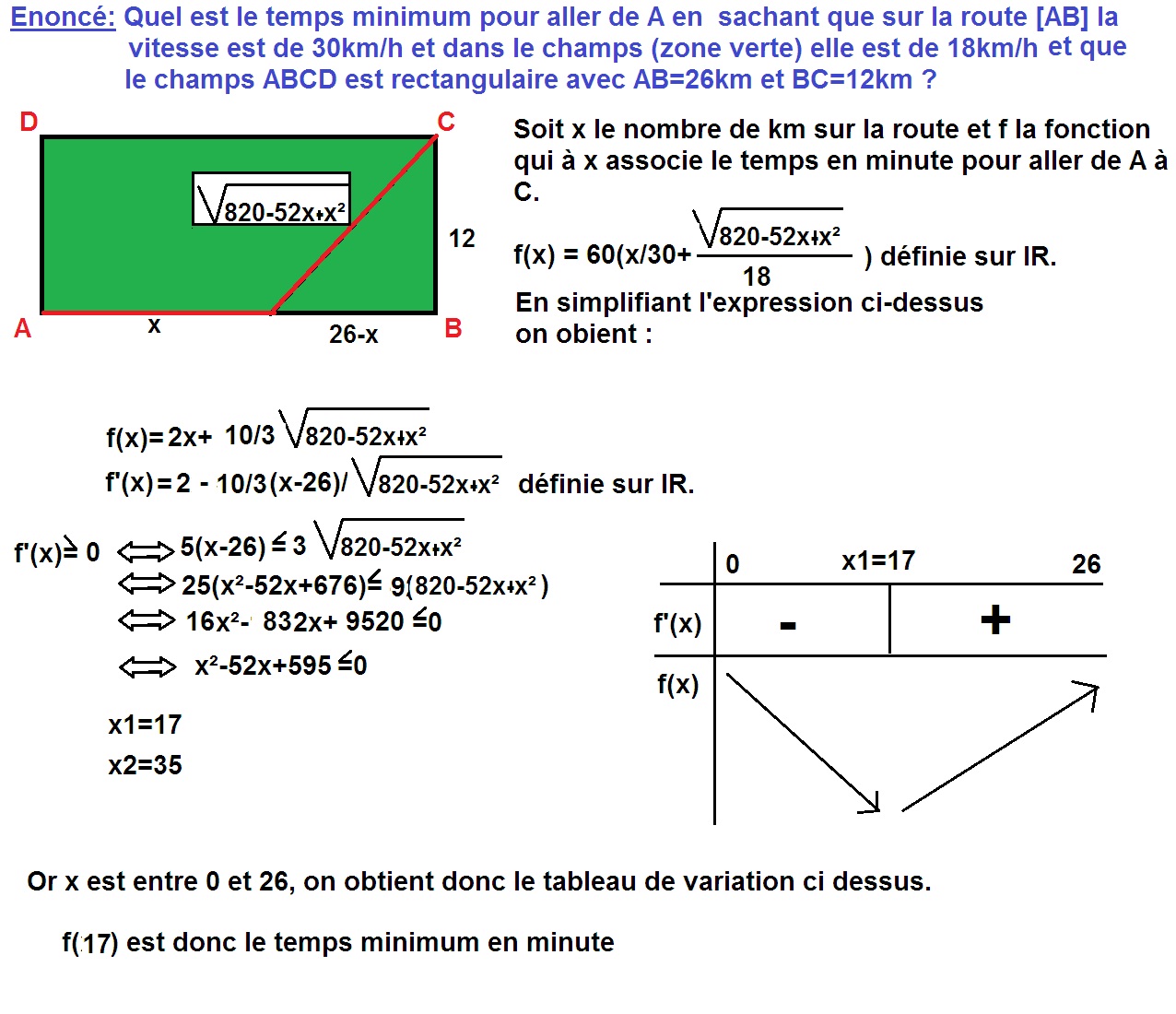
http://www.prise2tete.fr/upload/gilles355-champs.jpg
f(17)=84 minutes soit 1h et 24 minutes 
#6 - 03-11-2012 21:07:05
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
Parcours en VVTT
L'ami Wolfram m'a épargné la dérivation.
17 km sur la nationale, puis on traverse le reste du champ en diagonale.
7/5 d'heure soit 84 minutes.
J'ai déjà vu plus ambitieux, comme 1000me message 
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#7 - 03-11-2012 21:16:38
- Passetemps
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 405
PParcours en VTT
Il part du point A et fait 9 kms sur la route.
Il prend ensuite le champ et fait 15 kms en direction du point C.
Il met pour cela 84 mn.
#8 - 04-11-2012 00:46:13
- Azdod
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 763
- Lieu: In this universe ... !!
Parcours enn VTT
Par un calcul différentiel, Tu dois marcher 17 Km sur la route AB avant d'aller directement à C (15 Km).
La durée minimale sera de 84 minutes.
Merci pour cette énigme 
"Zero is where everything starts ! Nothing would ever be born if we didn't depart from there"
#9 - 04-11-2012 01:41:12
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Parocurs en VTT
Si x est la distance à parcourir sur la route AB, il faut rechercher le minimum de la fonction [latex]\frac{1}{18} \sqrt{144+(-26+x)^2}+\frac{x}{30}[/latex]
Je passe le calcul de la dérivée et la résolution de l'équation.
Le minimum de 84 (min) est atteint pour x = 17 (km)
#10 - 04-11-2012 16:59:50
- franck9525
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1935
- Lieu: 86310
Parcours en VTTT
le VTTiste suit la route de A vers B puis à une distance X de B, coupe à travers champ pour rejoinde C. Le temps de parcours devient:
t=60[ (26-X)/30 + (x^2+12^2)^(1/2)/18 ]=52-2X+10 V(x^2+12^2)/3
dt/dX=-2+(10 X)/(3 sqrt(144+X^2))
qui a pour racine X=9.
Le temps de parcours est 84 minutes losrque le cycliste ccoupe au km17.
The proof of the pudding is in the eating.
#11 - 04-11-2012 17:58:10
- elpafio
- Elite de Prise2Tete
- Enigmes résolues : 43
- Messages : 1018
Parours en VTT
Durée minimale de parcours: 84 minutes.
Je prends la route partant de A et me dirigeant vers B, puis, au bout de 17 km, je coupe en ligne droite à travers champ pour me diriger vers C.
Soit X la distance en mètres parcourue sur la route AB.
Soit Y le temps du parcours total en minutes.
[TeX]Y = (1/60) * (((3600 * X) / 30000) + ( 3600 * ( (1/18000) * \sqrt ( (26000 - X)² + 12000² )))) [/TeX]
En simplifiant, puis en calculant la dérivée, on doit parvenir à trouver le minimum Y=84 pour X=17000
#12 - 04-11-2012 18:13:46
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
parcoirs en vtt
Le trajet optimal est forcément constitué de deux segments :
1) une partie de [latex]26-x[/latex] km sur la route, à la vitesse de [latex]2[/latex] min/km
2) une partie de [latex]\sqrt{x^2+12^2}[/latex]km sur le champ, à la vitesse de [latex]10/3[/latex] min/km.
On cherche donc à minimiser [latex]f(x)=2(26-x)+\frac{10}3\sqrt{x^2+12^2}[/latex]
pour [latex]x \in [0;26][/latex]
On calcule [latex]f'(x)=-2+\frac{10x}{3\sqrt{x^2+12^2}}[/latex]
Alors, [latex]f'(x)=0[/latex]
[TeX]\Longleftrightarrow 2 = \frac{10x}{3\sqrt{x^2+12^2}}[/TeX][TeX]\Longleftrightarrow 6\sqrt{x^2+12^2} = 10x[/TeX][TeX]\Longleftrightarrow 6^2\times(x^2+12^2) = 100x^2[/TeX][TeX]\Longleftrightarrow 6^2\times 12^2 = 64 x^2[/TeX][TeX]\Longleftrightarrow 6\times 12 = 8x[/TeX][TeX]\Longleftrightarrow x=9 [/TeX][TeX]26-9=17
[/TeX]
Le trajet le plus rapide consiste donc à rouler 17km sur la route puis à se diriger vers le point d'arrivée.
[TeX]f(9)=2\times 17+\frac{10}3\sqrt{9^2+12^2}=34+10\sqrt{3^2+4^2}=34+10\sqrt{25}=34+50=84[/TeX]
Le temps de parcours minimal vaut alors 84 minutes.
#13 - 04-11-2012 18:20:12
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
paecours en vtt
La voie analytique est assez classique. En revanche, je ne vois pas de solution géométrique, et pourtant....
Sinon, je dirais 84 mn, en roulant sur la route pendant 17 kms.
#14 - 04-11-2012 20:40:23
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Parcorus en VTT
Solution générale du problème :
Soit le rectangle suivant : 
Vous pouvez vérifier que :
[TeX]BC=x[/latex] et [latex]BE=\frac{x}{2}[/TeX]
[TeX]FE=\frac{x*tan(\theta)}{2}[/TeX]
[TeX]z=y-x*tan(\theta)[/TeX]
[TeX]t=\sqrt{\left(\frac{x*tan(\theta)}{2}\right)^2+\left(\frac{x}{2}\right)^2}=\frac{1}{2}\left|\frac{x}{cos(\theta)}\right|[/TeX]
Calcul de la minimisation :
La longueur du trajet est minimal si [latex]4t+z[/latex] est minimal, c'est-à-dire si
[TeX]f(\theta)=2*\left|\frac{x}{cos(\theta)}\right|+y-x*tan(\theta)[/latex] est minimale.
On calcul : [latex]\frac{d}{d\theta}\left(f(\theta)\right)[/TeX]
Ce qui abouti à : [latex]\frac{2x^2tan(\theta)sec^2(\theta)}{\sqrt{x^2sec^2(\theta)}}-x.sec^2(\theta)[/latex]
Qui s'annule en [latex]\frac{\pi}{6}[/latex] et [latex]\frac{5\pi}{6}[/latex] avec [latex]x \neq 0[/latex]
Temps de parcourt :
En passant par la route sur la distance [latex]z=19.1[/latex] km et dans le champs sur la longueur [latex]2t=14[/latex] km
Il faudra donc [latex]\frac{14}{18}+\frac{19}{30}=1.41[/latex]h soit 84 minutes en faisant le calcul exact!
Shadock 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#15 - 05-11-2012 00:54:26
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Parours en VTT
Sans grande surprise, il n'y a que des bonnes réponses. J'avais trouvé cet exercice pour mes élèves de TF3 lorsque j'étais maître auxilliaire à la fin de mes études (en 1985 !!) et l'application pratique de la recherche d'un optimum leur avait bien plu.
#16 - 05-11-2012 11:18:19
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
parcours en vyt
J'ai cherché (peut-être mal) sur internet, c'est quoi TF3 ?
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#17 - 05-11-2012 11:28:59
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Paarcours en VTT
TF3 = Terminale section électrotechnique (en lycée technique). Mais cette filière a peut-être été renommée maintenant (comme mon vieux bac C).
#18 - 05-11-2012 12:35:30
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Parcours en VTTT
Et oui, le nom a changé.
Il s'agit maintenant de la Terminale STI électrotechnique (STI signifiant sciences et technologies industrielles).
#19 - 07-11-2012 00:14:05
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
PParcours en VTT
shadock ne trouve pas pareil que les autres non ?
#20 - 07-11-2012 00:33:41
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
Parcours en VT
Il a le même résultat mais en plaçant la route au milieu du champ 
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#21 - 07-11-2012 09:12:14
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Parcour en VTT
Effectivement, shadock a axé la route sur le champ, les points de départ et d'arrivée étant alors en plein champ, ce qui ne change pas le résultat final, même si ce n'est pas tout à fait l'énigme proposée.
J'ai aussi cherché une solution géométrique, comme suggéré par nodgim, en faisant une similitude avec des angles de réfraction, lorsque qu'un rayon lumineux passe d'un milieu à un autre, mais je n'y suis pas arrivé.
#22 - 07-11-2012 11:14:15
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Parccours en VTT
Il trouve 19 km sur la route et 14km dans les champs, au lieu de 17 et 15.
Mais j'ai trouvé une erreur : il minimise 4t+z au lieu de 2t+z.
#23 - 07-11-2012 16:08:07
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
patcours en vtt
J'étais en vacances. Dommage...
Au fait dans ces solutions, on présuppose que la meilleure solution est de suivre le bord puis d'obliquer en ligne droite. Mais comment prouve-t-on que c'est bien la stratégie qui va donner la meilleure solution?
D'autre part, cela ressemble un peu à un problème d'optique et de marche lumineuse d'un rayon. On pourrait en faire une énigme pour un 2000ème message  où le terrain est en pente et qu'il est de plus en plus boueux au fur et à mesure de la descente vers l'arrivée et que donc la vitesse décroit linéairement suivant la largeur du terrain. où le terrain est en pente et qu'il est de plus en plus boueux au fur et à mesure de la descente vers l'arrivée et que donc la vitesse décroit linéairement suivant la largeur du terrain.
#24 - 07-11-2012 16:36:42
- Azdod
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 763
- Lieu: In this universe ... !!
parxours en vtt
rivas a écrit:Mais comment prouve-t-on que c'est bien la stratégie qui va donner la meilleure solution?
C'est évident ! Si on quitte la ligne AB alors on est plus à 30 km par h et dans ce cas le meilleur parcours reste la diagonale AC (inégalité triangulaire)
Si jamais on marche X kilomètres sur AB et puis on la quitte on a intérêt à se diriger en ligne droite vers C pour les mêmes raisons !
C'est bien l'optimum car on suppose marcher sur AB avant d'aller linéairement à C !
"Zero is where everything starts ! Nothing would ever be born if we didn't depart from there"
#25 - 07-11-2012 16:50:27
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
PParcours en VTT
Que se passe-t-il si la route va de A à B puis de B à C ?
Y a-t-il des configs (vitesses route et champ, longueurs AB et BC) qui font qu'on a intérêt à faire un parcours route-champ-route ?
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum








