 |
#1 - 14-11-2012 19:41:32
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#2 - 14-11-2012 21:57:59
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
zchecs 21
C'est impossible.
Supposons qu'on ait trouvé une suite de retournements qui convienne.
Bon déjà remarquons que toutes les actions commutent et sont involutives.
On note [latex]l_i[/latex] (resp. [latex]c_i[/latex] et [latex]d_i[/latex]) le nombre de fois où l'on a appliqué le retournement [latex]L_i[/latex] (resp. [latex]C_i[/latex] et [latex]D_i[/latex])
On peut supposer que ces nombres sont égaux à 0 ou 1 sans perte de généralité.
On note [latex]\bar x = 1-x[/latex]
En considérant le pion [latex]M_{12}[/latex] (1ère ligne 2ème colonne), qui a dû être retourné exactement une fois, on peut établir que [latex]l_1 + c_2 = 1[/latex], ce que l'on peut noter [latex]l_1=\bar {c_2}[/latex].
On établit de même que [latex]l_1=\bar {c_2} = \bar {c_3} = \bar {c_4}[/latex]
puis [latex]l_2=\bar {c_1} = \bar {c_3} = \bar {c_5}[/latex]
donc [latex]c_1=c_2=c_3=c_4=c_5[/latex] et par symétrie [latex]l_1=l_2=l_3=l_4=l_5=\bar {c_1} = \bar {c_2} = \bar {c_3}=\bar {c_4} = \bar {c_5}[/latex].
En considérant le pion [latex]M_{11}[/latex], on en déduit que [latex]d_1=0[/latex] et de même [latex]d_2=0[/latex].
Par conséquent, [latex]M_{33}[/latex] n'a été retourné qu'une seule fois. On arrive à une contradiction.
#3 - 14-11-2012 22:53:53
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Echecs 12
C'est bon Titou 
On peut faire plus simple , je donnerai un indice dans quelque temps si personne n'y pense .
Vasimolo
#4 - 14-11-2012 23:11:59
- franck9525
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1935
- Lieu: 86310
rchecs 21
Il est possible d'associer le probléme à des additions matricielles en base 2.
En admettant rouge=1 et bleu=0 par exemple.
L'addition étant commutative, il est inutile de retourner deux fois la même série.
les jetons de coordonnées (1,2) ainsi que les 7 symétriques ne peuvent être retourner que par une ligne ou une colonne, mais pas les deux. Il en est de même pour les milieux (1,3) (2,3), etc.
Si je retourne la premiére ligne, je ne peux retourner les colonnes 2,3 et 4 ce qui m'oblige à retourner les lignes 2, 4 et 5 empêchant alors de retourner les colonnes restantes. Le probléme n'a donc pas de solution.
The proof of the pudding is in the eating.
#5 - 14-11-2012 23:16:35
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Echeecs 21
Franck , tu as noté que les retournements sur les deux diagonales étaient autorisés ?
Vasimolo
#6 - 15-11-2012 17:57:16
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
zchecs 21
C'est drôle, mais je trouve que c'est impossible.
On peut dire que les valeurs (si N=0 et B=1) des cases sont le résultat d'un code donné par les 5 lignes, les 5 colonnes et les 2 diagonales: Le résultat des cases correspond à la somme modulo 2 des 2 à 4 codes.
Si, pour le carré 3*3, il est aisé de retrouver le code des 3 lignes, 3 colonnes et 2 diagonales, pour le carré 5*5, on se rend assez vite compte que c'est impossible.
J'ajoute que le nombre de codes possible fourni par les 12 L+C+D est 2^12, alors que le nombre de configurations possibles dans le carré est de 2^25.
Il est donc normal de trouver des configurations qui ne correspondent à aucun code. Bien entendu, le "toutes les cases à 1" est un code possible.
#7 - 15-11-2012 18:16:29
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,192E+3
Echecs 1
Je pense que ce n'est pas possible.
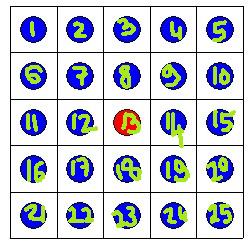
Si on retourne la ligne 1, on ne peut plus toucher aux colonnes 2 3 4 (pour la parité des retournements des cases 2 3 et 4)
Et donc, on doit retourner aussi la ligne 2 (case 8), la ligne 3 (cases 12 et 14) , et les lignes 4 et 5 (cases 18 22 23 24 )
Au bout du compte on retourne toutes les lignes et il ne reste qu'une diagonale sur les 2 comme option pour garder la case 13 en rouge.
Par symétrie du problème, on ne peut donc pas retourner une ligne ou une colonne du bord.
Mais alors pour les cases 2 3 4 6 11 16 22 23 24 10 15 20 ?
Il faut retourner toutes les autres lignes et colonnes Sauf que les cases 8 12 14 et 18 changent 2 fois.. Raté !
#8 - 15-11-2012 19:43:36
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Echcs 21
@Nodgim : il est évident que toutes les configurations ne sont pas réalisables mais pourquoi celle-ci justement ?
@Gwen : c'est bon et plutôt simple 
On parlait d'invariants à propos du problème précédent , ici il y en a un qui donne la réponse sans effort mais il faut le dénicher 
Vasimolo
#9 - 15-11-2012 23:11:39
- godisdead
- Expert de Prise2Tete
- Enigmes résolues : 22
- Messages : 747
Echesc 21
Sur ce carré 5*5, il existe 12 coups possibles.
Chaque pion doit être rétourné un nombre impair de fois pour passer au rouge, sauf celui du centre qui doit être retourné un nombre pair de fois !
Le centre peut etre retourné 4 fois, les diagonales, 3 fois et les autres cases, 2 fois !
Je vais surtout m'intérresser à ces 16 points pair.
Si je commence par la colonne 1, il m'est alors interdit de toucher aux ligne 2/3/4 !
Donc je suis obligé de retourner les colonnes 2,3, 4 et 5.
Bref, c'est mort !
Par symétrie, je n'ai pas le droit de toucher aux colonnes 1 et 5, ni aux lignes 1 et 5.
Je dois alors retourner la ligne 3 (et la colonne 3), cela me bloque les ligne 2/4 et les colonnes 2/4 !
Là aussi, j'arrive à une impossibilitée. L'utilisation des diagonales ne changent rien à mon affaire.
Pour moi, c'est impossible.
#10 - 16-11-2012 12:01:15
- nobodydy
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1677
echecd 21
Après 2 heures sur Power point a jouer à changer les couleurs de mes petits ronds.
Je sents que c'est impossible !!!
mais pourquoi ??
aucune idée pour le moment !
 
#11 - 16-11-2012 12:08:12
- nobodydy
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1677
Echcs 21
une idée
si c'est possible alors , ce message ne sert à rien
mais si c'est impossible
il doit y avoir un truc mathématique du style 2 puissance N
il y a 8 bleu au départ, donc 2 puissance 3
mais l'enigme a 24 bleus donc pas de 2 puissance x
mes maths sont loins ...... très loin...
#12 - 16-11-2012 19:15:29
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Echhecs 21
@godisdead : c'est bon 
@Nobody : il faut creuser un peu plus .
Vasimolo
#13 - 17-11-2012 22:50:25
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Ecehcs 21
Pour ajouter ma solution à celles déjà données . On pose un cache sur le jeu et on ne tient plus compte des cases recouvertes par les croix :

Chaque coup laisse invariant la parité de pions de chaque couleur . Au début il y a une case rouge et la position finale attendue devrait laisser apparaître vingt cases rouges : c'est impossible .
Merci à tous pour les solutions très originales 
Vasimolo
#14 - 18-11-2012 12:10:48
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
echexs 21
Sympa ta solution !
Merci pour l'énigme.
#15 - 18-11-2012 13:59:50
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Echecs 2
Ah oui, cet invariant de parité avec des cases masquées, il fallait le trouver.
#16 - 18-11-2012 20:29:08
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Echecss 21
Oufff !
Ah oui, très joli en effet. Je me délecte toujours des réponses malgré mon incapacité à trouver la solution. J'adore ! 
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum










